一种光纤陀螺随机噪声时间序列建模与实时滤波方法

胡俊伟, 刘明雍, 张加全



一种光纤陀螺随机噪声时间序列建模与实时滤波方法

胡俊伟, 刘明雍, 张加全

(西北工业大学 航海学院, 陕西 西安, 710072)

为了减小光纤陀螺(FOG)的随机噪声, 利用时间序列分析法对FOG的随机噪声进行了分析与建模, 并在建立的自回归滑动平均(ARMA(2,1)）模型基础上, 采用一种将改进递推增广最小二乘(RELS)算法和Sage-Husa自适应卡尔曼滤波算法相结合的方法, 对采集的FOG静态输出随机噪声进行实时补偿, 同时与标准kalman滤波算法进行仿真对比。仿真结果表明, 该方法具有更好的补偿效果, 可更有效地抑制FOG随机噪声。

光纤陀螺(FOG); 自回归滑动平均(ARMA)模型; 递推增广最小二乘法(RELS); Sage-Husa自适应卡尔曼滤波

0 引言

光纤陀螺(fiber optic gyro, FOG)是基于Sagnac干涉原理测量载体旋转角速度的敏感元件。以其启动快、耐冲击、灵敏度高、动态测量范围宽、使用寿命长等突出优点在惯导系统中得到广泛的应用。但由于材料工艺、加工工艺等条件的限制,当前市场中绝大部分FOG都是中低精度的, 难以满足高精度惯性导航的要求[1]。通过对陀螺随机噪声进行补偿来提高FOG的测量精度, 弥补FOG工艺质量上的缺陷, 是进一步提高光纤陀螺精度所面临的主要问题。因此, 对FOG的随机噪声进行建模补偿具有十分重要的意义。

FOG随机噪声是一个十分复杂的随机、时变过程, 且不易消除。静态放置下FOG的输出可以看成是一个随机噪声序列, 其特性对建模及补偿具有重要的影响。本文采用时间序列分析法直接对FOG实测信号进行建模, 针对利用观测数据建立的FOG随机噪声自回归滑动平均(auto regression moving average, ARMA)模型存在一定误差, 提出采用一种将改进的递推增广最小二乘算法(recursive extended least squares, RELS)和Sage-Husa自适应Kalman滤波算法相结合的方法, 对采集的FOG静态输出随机噪声进行实时补偿。仿真结果表明, 该方法具有良好的补偿效果,可实现对中低精度FOG随机噪声的有效抑制。

1 FOG随机噪声ARMA建模

1.1 基于时间序列分析的ARMA模型

时间序列分析是对有序的随机数据进行分析和研究的现代统计分析方法, 即将现在时刻的值用过去时刻的值表示, 然后预测系统的未来值。时间序列分析方法的基本模型是自回归滑动平均(auto regression moving average, ARMA) 模型, ARMA()模型可表示为[2]

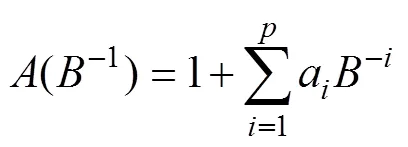
ARMA)模型是针对平稳时间序列的时序分析模型, 但中低精度光纤陀螺静态输出的随机噪声是非平稳的时间序列, 所以在建模之前必须对数据进行平稳化处理[3]。在实验室条件下, 将某型低精度单轴FOG静态水平放置, 在输出量中减去地球自转的天向分量, 得到一组FOG静态随机噪声测试数据(见图1)。

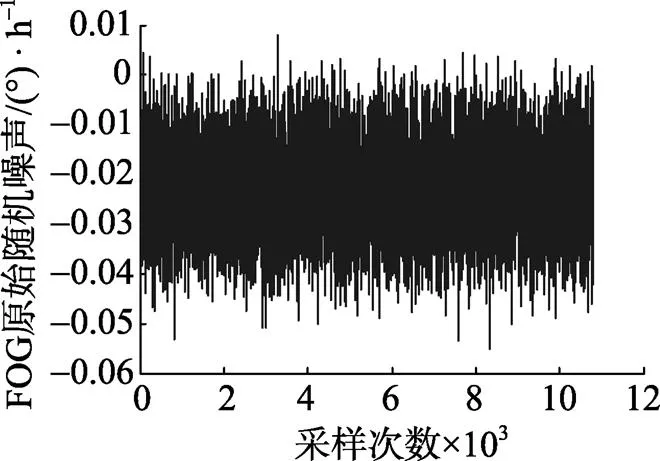
图1 FOG原始随机噪声

对该组数据构成的随机噪声序列作1阶差分处理得到的时间序列如图2所示。对差分后的序列进行零均值、平稳性及正态性假设检验, 结果符合ARMA建模要求。

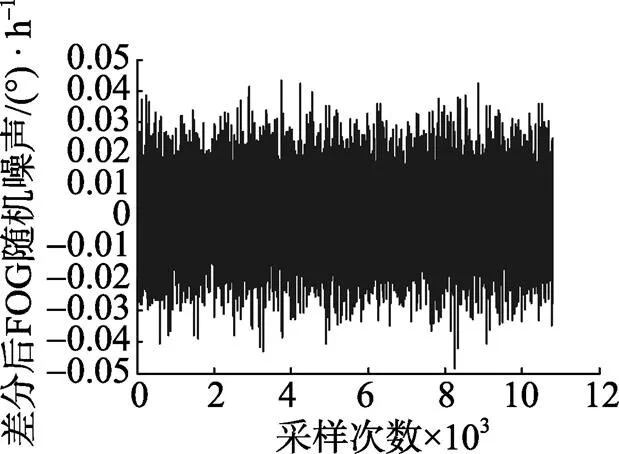
图2 1阶差分后FOG随机噪声

建立FOG随机噪声的ARMA(,)模型,首先要判断模型的阶次。最终预报误差(final rediction error, FPE)准则和赤池信息量（akaike information criterion, AIC）准则是判断模型阶次的常用方法。本文采用Akaike的AIC准则[4], AIC定阶准则的定义为

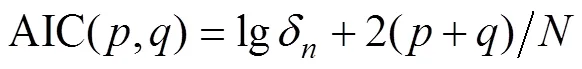
式中:是拟合残差的方差;，分别是自回归(auto regression, AR) 模型和滑动平均(moving average, MA)模型部分的阶次;是参与估计样本个数。

AIC准则全面考虑了模型阶次和残差的相互作用, 同时将建模数据长度对模型的影响纳入其中, 具有很高的准确性。具体运用时, 由低到高分别计算不同阶次模型的AIC值, 然后选择AIC值最小的阶次建立系统模型。由于FOG随机噪声模型的阶次都较低, 一般不超过2~3阶, 因此可以在模型参数数目小于3的范围内, 取AIC最小值所对应的模型。实际应用中, 误差模型通常在AR (2)，AR (3)和ARMA (2, 1)中进行选择[5,6]。

1.2 ARMA模型的参数递推估计算法

对FOG随机噪声的补偿是一个动态的过程, 所以样本数据的模型参数也是动态变化的, 把随机噪声模型即式(1)写成矩阵的形式

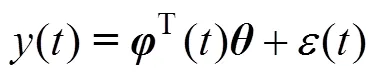
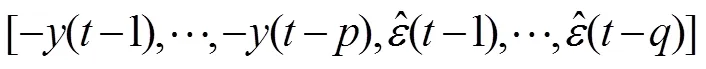
设原ARMA()模型可以用AR()来拟合,一般取很大的值(=10～20), 则

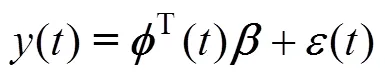
其中,T=[-(-1),…,-(-)],T=[1,…,a], 由RLS算法可得

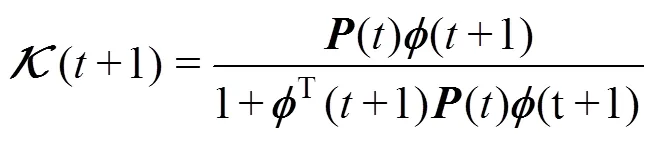
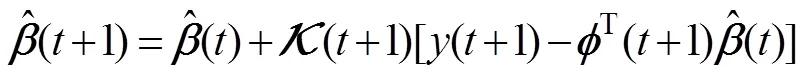
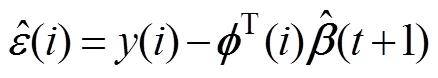
取2 000组FOG静态随机噪声数据, 用改进的RELS算法对拟定的AR(2)、AR(3)和RMA(2,1)模型参数进行估计, 仿真结果见表1。从RELS估计的AIC值可以定量地说明ARMA(2,1)模型的精度更能够反映FOG随机噪声的特性。

表1 FOG随机噪声各模型参数及AIC值

2 基于ARMA模型自适应Kalman滤波算法

根据得到的ARMA(2,1)模型,可利用Kalman滤波对中低精度FOG的随机噪声进行抑制。但Kalman滤波要求精确的系统数学模型和噪声统计, 不准确的系统模型和噪声统计常常引起滤波发散。由于FOG的随机噪声受多种因素影响, 其统计特性往往是时变或未知的, 利用观测数据建立的系统模型参数不可避免地存在误差。针对上述问题, 本文尝试采用Sage-Husa自适应Kalman滤波算法来提高FOG随机噪声的估计精度。

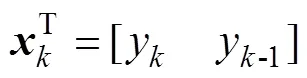
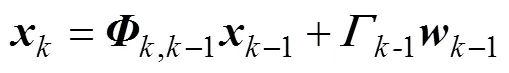
设v为ARMA(2,1)模型表示真实时间序列的估计误差, 则系统的量测方程为

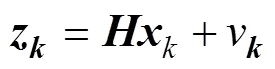
式中:=[1 0]为观测矩阵；量测噪声v和系统噪声w为互不相关的白噪声序列, 且均值分别为r和q；方差分别为R和Q。

针对式(9)和式(10)描述的带有时变噪声统计的离散系统, 采用Sage-Husa自适应Kalman滤波算法即可获得FOG随机噪声的精确估计。该滤波算法的极大后验噪声统计估值器为

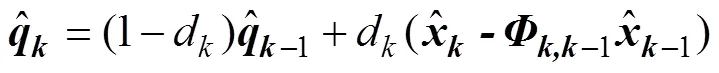
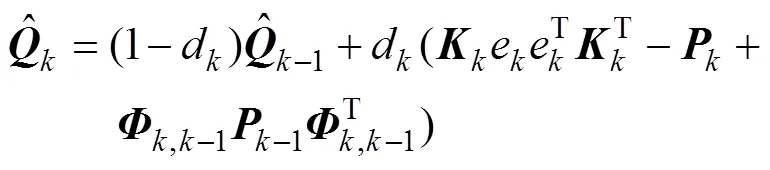
其中:d=(1-)/(1-b+1),为经过试验确定的遗忘因子。

将式（11）~式（14）与常规的Kalman滤波方程联立即可得Sage-Husa自适应Kalman滤波算法[8]。该算法可在线估计噪声特性和状态向量, 而且具有良好的收敛效果, 在工程中被广泛采用。

3 FOG随机噪声实时补偿

将改进的RELS的算法和Sage-Husa自适应Kalman滤波结合起来, RELS用于根据实时输入的噪声信号不断的更新滤波器的系统状态转移矩阵, 自适应Kalman滤波可以弥补由于时间序列模型误差带来的估计精度损失。但需要注意的是, Sage-Husa自适应Kalman滤波对滤波器的初值选取比较严格。而滤波开始时, 改进的RELS算法对模型的系数和方差的估计是不稳定的, 势必会使滤波器发散, 所以在RELS估计器的估值波动较大时, 可直接用时间序列模型的预测值作为噪声的估计值, 不使用自适应Kalman滤波。按上述方法对采集的FOG静态输出随机噪声进行补偿, 并与标准的Kalman滤波算法进行对比, 仿真结果如图3, 图4以及表2所示。图中的曲线表示滤波后的FOG随机噪声。表2给出了滤波前后FOG随机噪声的统计特性对比。

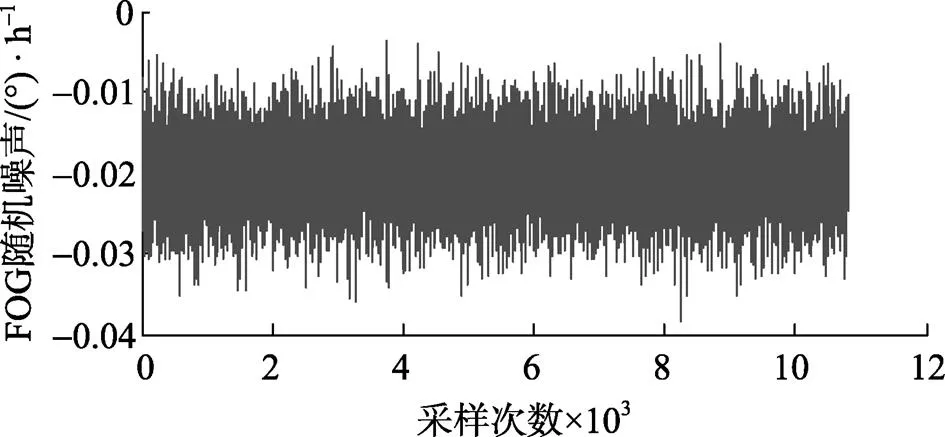
图3 标准Kalman滤波后的FOG随机噪声

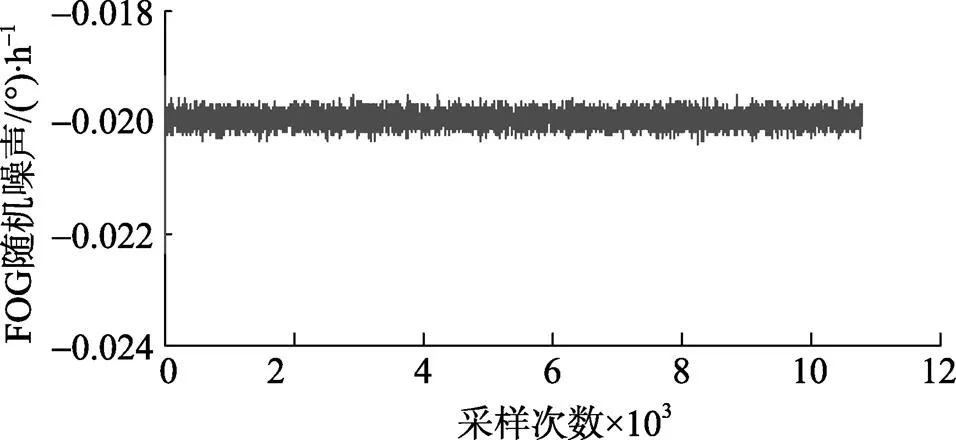
图4 Sage-Husa自适应Kalman滤波后的FOG随机噪声

表2 FOG随机噪声滤波前后统计特性比较

比较图1、图3和图4可看出, 滤波后FOG的随机噪声明显变小。同时, 从表2也可定量地看出, 经标准Kalman滤波和Sage- Husa自适应Kalman滤波后, 数据的均值基本没有变化, 方差比滤波前分别减小了1个和3个数量级。这说明试验采用的滤波方法可在保证无偏估计的同时使数据的分散程度显著地减小, 且Sage-Husa自适应Kalman滤波的效果明显优于标准Kalman滤波。通过以上分析可以说明, 本文采用的Sage-Husa自适应Kalman滤波具有更高的估计精度, 对FOG的随机噪声具有更好的抑制作用。

4 结束语

本文采用时间序列分析法对中低精度FOG的实测数据进行了分析和建模。在确定FOG随机噪声模型为ARMA(2,1)模型的基础上, 将改进的RELS的算法和Sage-Husa自适应Kalman滤波相结合, 实现对FOG实际输出信号的消噪处理。仿真结果表明, 采用该方法能够有效地抑制FOG输出信号的随机噪声, 对于提高惯性导航精度具有重要意义。

[1] Lefevre H C. The Fiber-optic Gyroscope[M]. Artech house, 1993.

[2] 王雪平, 李俊, 张福斌. 基于时间序列分析方法的FOG随机噪声建模与辨识[J]. 鱼雷技术, 2007, 15(4): 34-37.Wang Xue-ping, Li Jun, Zhang Fu-bin. Modeling and Identifying of Fiber Optic Gyro Random Drift Data Based on Time Series Analysis Method[J]. Torpedo Technology, 2007, 15(4): 34-37.

[3] Sameh N, Klaus-peter S, Naser E,et al. Modeling Inertial Sensor Errors Using Autoregressive (AR) Models[J]. Navigation, 2004, 51(24), 259-268.

[4] Broersen P M T, de Waele S. Costs of Order Selection in Time Series Analysis[C]//Instrumentation and Measurement Techn- ology Conference. Proceedings of the 19th IEEE, 2002: 303-308.

[5] 陈涛, 王新龙, 杜宇. 基于AR模型的光纤陀螺建模方法研究[J]. 鱼雷技术, 2005, 13(3): 24-27. Chen Tao, Wang Xin-long, Du Yu. Modeling Method of Fiber Optic Gyro Based on AR Model[J]. Torpedo Technology, 2005, 13(3): 24-27.

[6] 李晓峰, 徐军, 张胜修. 光纤陀螺随机误差建模与滤波方法研究[J]. 光学技术, 2008, 34(s): 179-180. Li Xiao-feng, Xu Jun, Zhang Sheng-xiu. Study on the Modeling and Filter of the Fiber-optical Gyroscope Random Error[J]. Optical Technique, 2008, 34(s): 179-180.

[7] 邓自立. 自校正滤波理论及其应用--现代时间序列分析方法[M]. 哈尔滨:哈尔滨工业大学出版社, 2003.

[8] 张常云. 自适应滤波方法研究[J].航空学报, 1998, 19(7): 96-99.Zhang Chang-yun. Approach to Adaptive Filtering Algorithm [J]. Acta Aeronautica et Astronautica Sinica, 1998, 19(7): 96-99.

A Time Series Modeling and Real Time Filtering Method for FOG Random Noise

HU Jun-wei, LIU Ming-yong, ZHANG Jia-quan

(College of Marine Engineering, Northwestern Polytechnical University, Xi¢an 710072, China)

In order to reduce the random noise of fiber optic gyroscope (FOG), the random noise of FOG is analyzed and modeled by time series analysis method. Based on the established auto regression moving average（ARMA）(2, 1) model, a method that combines modified recursive extended least squares (RELS) algorithm and Sage-Husa adaptive Kalman filter algorithm is proposed to compensate the static output random noise of FOG in real-time. In addition, the standard Kalman filter algorithm is used for comparison. Simulation results show that the proposed method achieves better compensation effect and more effective inhibition of the FOG random noise.

fiber optic gyroscope(FOG); auto regression moving average(ARMA) model; recursive extended least squares(RELS); Sage-Husa adaptive Kalman filter

TJ630.33

A

1673-1948(2011)01-0031-04

2010-05-20;

2010-07-05.

国家自然科学基金(50979093)，新世纪优秀人才计划资助(NCET-06-0877).

胡俊伟(1985-), 男, 在读硕士, 研究方向为水下航行器惯性导航与制导.

(责任编辑: 杨力军)