基于遗传算法的PID 参数整定
2011-05-24张淑娟
张 力,魏 静,张淑娟
(山东电力工程咨询院有限公司,山东 济南 250013)
0 引言
PID控制是工业过程控制中应用最广的策略之一,因此PID控制器参数的优化成为人们关注的问题,它直接影响控制效果的好坏,并和系统的安全、经济运行有着密不可分的关系。目前PID参数的优化方法有很多,如间接寻优法、梯度法、爬山法等,而在热工过程中单纯形法、专家整定法则应用较广。虽然这些方法都具有良好的寻优特性,但存在着一些弊端,单纯性法对初值比较敏感,容易陷入局部最优解,造成寻优失败。专家整定法则需要太多的经验,不同的目标函数对应不同的经验,而整理知识库则是一项长时间的工程。
遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。
采用遗传算法进行PID系数的整定,具有以下优点:
1)与单纯形法相比,遗传算法同样具有良好的寻优特性,克服了单纯形法对参数初值的敏感性。在初始条件选择不当的情况下,遗传算法在不需要给出调节器初始参数的情况下,仍能寻找到合适的参数,使控制目标满足要求。同时单纯形法难以解决多值函数问题以及在多参数寻优 (如串级系统)中,容易造成寻优失败或时间过长,而遗传算法的特性决定了它能很好的克服以上问题。
2)与专家整定法相比,它具有操作方便、速度快的优点,不需要复杂的规则,便可实现寻优,避免了专家整定法中前期大量的知识库整理工作及大量的仿真实验。
3)遗传算法是从多点开始并行操作,在解空间进行高效启发式搜索,克服了从单点出发的弊端及搜索的盲目性,从而使寻优速度更快,避免了过早陷入局部最优解。
4)遗传算法不仅适用于单目标寻优,而且也适用于多目标寻优。根据不同的控制系统,针对一个或多个目标,遗传算法均能在规定的范围内寻找到合适参数。
1 简单PID控制器的参数整定
热工过程自动控制是保证热力设备安全和经济运行的必要措施和手段,目前热工过程自动控制广泛采用的控制策略是经典PID控制,其算法简单、鲁棒性好且可靠性高,尤其适用于可建立精确模型的确定性控制系统。随着火电机组单机容量和参数的不断提高,系统变得日趋复杂,热工过程越来越表现出非线性、慢时变、大迟滞、强耦合性和不确定性,这对热工过程自动控制系统则提出了更高的要求,传统的PID控制已经无法满足这种要求,必须采用先进的控制策略进行优化控制。
设计先进控制系统时,必须首先考虑控制系统的安全性和可靠性。操作人员对手动及PID控制比较熟悉,有一定的操作经验,但对预测控制等先进控制技术比较陌生,所以在先进控制策略的具体实施时,要充分考虑操作人员的适应性,要保留原PID控制及手动控制。在先进控制算法出现意外情况下,可以方便地切换到手动控制或PID控制,保证设备安全可靠运行。
因此,首先使用遗传算法对简单 PID控制器的参数进行整定。
1.1 基于遗传算法的PID参数寻优基本步骤
1)编码设计。利用遗传算法进行 PID参数优化,首先要将待优化参数编码成个体的表示串。对于此例,需优化的 PID 参数为 kp、ki、kd。
2)适应度函数。
控制器参数的优化是相对于一定的性能指标而言的。本例采用的性能指标为:

目标函数确定后,遗传算法即可以此来确定适应度函数

1.2 仿真试验
吴泾第二发电厂1号机组(600 MW机组)再热减温喷水阀开度变化 Δ μ(%),对再热喷水减温器出口导前汽温变化 ΔT1(℃)、对再热器前墙出口两侧温度变化 ΔT2(℃)及对末级再热器出口汽温变化 ΔT(℃)的动态数学模型为[1]
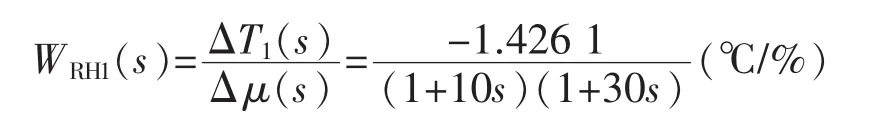

因此,再热减温喷水阀开度变化Δ μ(%)对末级再热器出口汽温变化 ΔT(℃)的动态数学模型为


图1 仿真试验过程曲线
控制器参数的寻优范围为:kp∈(0.01,1.8),ki∈(0.001,0.01),kd∈(20,50)。遗传 算法相应的控制参数为:种群规模N1=30,N2=30,最大遗传代数G=35。通过寻优得到:kp=1.514 2,ki=0.007 8,kd=35.619 6。阶跃响应曲线和控制作用曲线如图1所示。
由于锅炉再热汽温是高阶、大惯性的被控对象,其动态响应过程比较慢,为保证控制系统的稳定性,调节器只能整定得很慢,从而使控制品质很差。为既要保证控制系统的稳定性,又要使调节器快速动作,只能通过对被控对象进行动态补偿,使通过补偿后的等效对象具有较好的动态特性,这实质上是内模控制的思想。可以采用能对大滞后特性进行动态补偿的两种先进控制技术-状态变量控制技术和相位补偿技术对其进行动态补偿。
2 基于大滞后补偿技术的PID控制器的参数整定
2.1 大滞后补偿技术
1)状态观测器的设计
通过对被控对象实施状态反馈,可以将被控对象闭环特征方程的根配置到希望的位置。即使被控对象具有较大的滞后,通过状态反馈,也可使经状态反馈补偿后的广义被控对象具有较好的动态响应特性 (即有效减小了原被控过程的惯性时间)。但是,状态反馈必须要知道系统的状态,而在实际的系统中状态变量往往是不能直接测量的,因此,必须通过状态观测器来重构真实对象的状态参数。
假设在再热器的流程上增加了 6个温度测点,各测点之间的再热器相对较短,因此,假定为一阶惯性环节,即为:G(s)=1/1+Ts,而整个再热汽温被控对象可近似为6阶多容惯性环节。
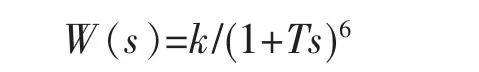
通过状态变量控制器的动态补偿后,整个等效对象的动态特性变化为:W(s)=β6k/1+βTs)6(0<β<1),式中,β反馈系数 fi具有一一对应的关系,不管用户选定多么小的 β值,总能计算出各反馈系数fi的值。可见,尽管状态变量控制器不能减少模型的阶次,但能有效减少等效对象的开环增益和惯性时间,从而在保证闭环系统相同稳定性的前提下,有效减小调节器的比例带和积分时间,加快调节器的动作速度。由于实际的再热汽温特性与数学模型间总是存在一定偏差,且扰动也无法直接作用在数学模型上,这就使得用数学模型估计出来的各点温度变化和实际过程有一定差别,为减少各点的温度差异,通过各状态观测环节Ki,逐步消除各点的温度偏差。状态变量控制器的参数fi和 Ki的具体计算方法可参见文献[2-3]。图2为状态变量控制技术原理示意图。

图2 状态变量控制技术原理示意图
2)相位补偿网络。
虽然状态变量控制可以等效的降低被控对象的时间常数,但状态反馈的补偿并不能降低被控对象的阶次,补偿后的广义被控对象仍然是6阶系统,PID控制器对于高阶对象的控制效果较差[4],而相位补偿网络的超前性能可以补偿被控对象的惯性和滞后,从而使补偿后的等效对象具有滞后较小的特性。
相位补偿环节的传递函数为:
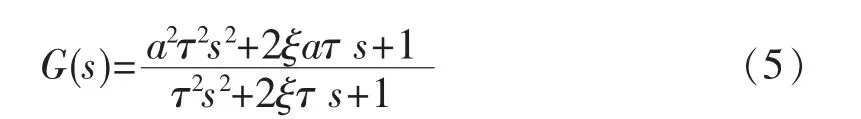
由于加入了相位补偿,使控制系统产处相角超前,从而使调节器的比例带减小后,也不致于过分降低系统稳定性,从而可提高控制品质。对相位补偿环节,需整定的参数有3个,即a、τ、ξ。参数选择原则为 a=3~5,ξ=0.7~1,τ=(0.3~0.5)T (假设被控对象是一个高阶的多容惯性环节,T为时间常数)[4]。一般而言,相位补偿网络可使补偿后的等效对象的模型阶次比原对象的模型阶次降低二阶。这样可在保证控制系统稳定性不变的前提下,加快调节器的动作速度,从而有效抑制被调量的变化。
因此,在对被控对象进行状态反馈补偿的基础上再进行相位补偿,可以进一步的改善整个系统的动态特性,提高控制品质。
2.2 仿真结果
图3中实线对应于基于大滞后补偿技术的PID控制器,虚线对应于简单PID控制器。可见,先应用大滞后补偿技术补偿被控对象的惯性和滞后,再采用遗传算法进行 PID控制器参数寻优,是提高控制效果的一种有效措施。
相关参数为:f=[2.571,2.755,1.574,0.506,0.087,0.006],a=4,ξ=0.7,τ=0.4T。
遗传算法相应的控制参数为:种群规模N1=30,N2=30,最大遗传代数G=35。通过寻优得到:kp=1.401 7,ki=0.016 1。

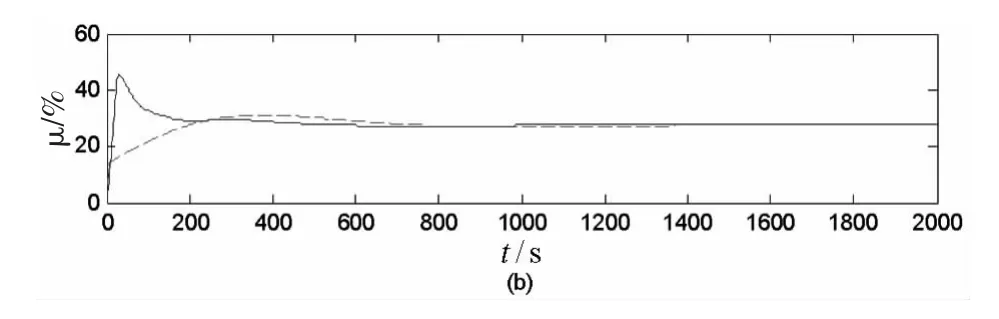
图3 仿真试验过程曲线
3 结语
在采用遗传算法对PID控制器参数进行寻优的基础上,引入大滞后补偿技术(状态变量技术和相位补偿技术),先补偿被控对象的滞后和惯性,再采用遗传算法寻优,取得了良好的效果。
