舞蹈机器人中音乐基音频率的提取
2011-05-21何晓亮秦文健
何晓亮,贾 亮,秦文健
(1.沈阳航空航天大学 电子信息工程学院,辽宁 沈阳 110136;2.中国科学院深圳先进技术研究院 医疗机器人与微创手术中心,广东 深圳 581055)
在舞蹈机器人中,要求机器人能够根据音乐表达出来的不同情感选择不同风格的舞蹈,能够跟随音乐的旋律、节奏、和鼓点等信息做出快速准确的舞蹈动作,这就要求对音乐信号的特征参数进行快速有效解析。音乐信号的特征参数可以分为3个层次,即音乐信号的基本特征、复杂特征和整体特征。音乐信号的基本特征参数包括音乐的音强、音长和音高等;复杂特征参数包括音乐的旋律、节奏和节拍等信息;整体特征参数包括音乐表达出来的情感等信息。在提取了音乐信号基本特征参数的基础之上,分析和提取音乐信号的复杂特征参数,进而分析和提取音乐信号的整体特征。音乐信号的音高作为音乐信号的基本特征参数,决定了音乐信号的旋律变化。而音乐音符的音高与音乐信号的基音频率是一一对应的关系,因此,音乐的基音频率是音乐信号特征参数识别中及其重要的参数之一。音乐信号的基音频率提取的质量对音乐的音高、节奏、旋律和情感等特征参数的提取具有重要的意义,将会直接影响到音乐信号特征参数提取的效果。作为音乐识别领域内重要的研究内容之一,目前常用的音乐信号基音频率的提取方法主要有自相关函数法(ACF)[1]、平均幅度差函数法(AMDF)[2]、倒谱法(CEP)和小波变换法[3]等,而单纯的利用自相关函数法或者平均幅度差函数法等一般都会产生一定的基音检测错误,采用自相关函数法提取音乐信号的基因频率,需要识别出自相关函数的峰值及峰值的位置,但是在自相关函数中,高次谐波的峰值可能会大于真实的基因频率对应的峰值,这样提取出来的峰值是错误的,会造成音乐信号基音频率提取错误,同时,自相关函数的计算需要计算大量的乘法运算,计算量较大,会影响到音乐信号基音频率提取的实时性;而采用平均幅度差函数法,虽然其运算复杂度较小,并且其在信号基音周期处的谷点也比较尖锐,有利于提高基音频率提取的精度,但是平均幅度差函数法对音乐信号幅度的快速变化非常敏感,也会影响基音频率提取的精度。近年来相关文献中提出了很多改进的基音频率的提取方法,文献[4]中提出对语音信号进行3层小波分解,并用小波系数加权法和互相关函数结合的方法提取语音的基音周期,取得了较好的效果;文献[5-7]中提出在频域和对数域中对音乐信号进行自相关处理的方法,可以较好地提取信号的基音频率;文献[8]中,提出了一种基于智能神经网络(Neural Network System)的基因频率提取方法,这种方法的提出相对于传统的神经网络基因频率提取的方法,能够实现对基音频率的有效提取,但是计算量较大实时性不强。
因此,笔者提出了一种基于自相关函数法的音乐信号基音频率提取的方法,即首先对音乐信号进行预处理,确定采样率以及帧长和帧移,消除工频干扰等噪声干扰,再对音乐信号进行切比雪夫滤波进一步消除噪声干扰,利用三电平中心削波[3]对音乐信号进行处理以减少自相关函数的计算量,进而利用两次计算音乐信号的自相关函数提取音乐的基音周期,从而提取音乐信号的基音频率。这种方法计算量小、提取速度快,提取准确,对音乐基音频率的提取效果较好,可以满足舞蹈机器人对音乐特征参数提取速度实时性的要求。
1 算法分析
基音频率提取的流程图如图1所示。
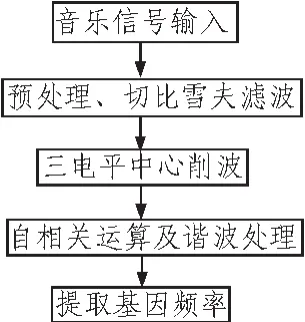
图1 基音频率提取的流程图Fig.1 Flow chart of pitch detection
1.1 预处理
音频信号的预处理一般包括预滤波、加窗分帧等。预滤波的目的是:1)抑制输入信号各频率分量中频率超过fs/2的所有分量(fs为采样频率),以防止混叠干扰;2)抑制50 Hz的电源干扰。预滤波处理相当于使用一个带通滤波器对信号进行处理。
进行数字预滤波之后要对音乐信号进行加窗分帧处理,分帧就是将音乐信号截取为短时段,便于利用稳态信号的计算方法进行计算,每一帧的长度一般取30~50 ms,为了使信号的帧与帧之间实现平滑过渡,保持其连续性,帧和帧之间要有所交叠,交叠的部分叫做帧移。帧移的长度一般为信号帧长的1/3~1/2,分帧的具体方法是利用一定长度的窗 函数 ω(n)去乘以信号 x(n),从而截取出一帧信号 sω(n)= ω(n)×s(n)。 常用的窗函数有矩形窗、海明窗和汉明窗等,本文采用矩形窗,窗长取值为30 ms,帧移为15 ms。矩形窗表达式如公式(1):
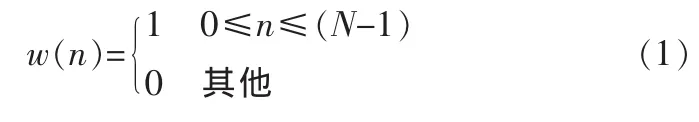
1.2 切比雪夫滤波
切比雪夫滤波器在语音分析、图像信号处理以及医学诊断等领域有着广泛的应用。切比雪夫滤波器可以从复杂的信号中提取出所需要的信号,抑制干扰信号。音乐信号中含有各种噪声和干扰,常用的滤波算法有滑动平均值法、算术平均值法、防脉冲干扰平均值法等,这些算法可以消除由于偶然激励引起的脉冲干扰,但是它们对于环境噪声以及电源的工频干扰效果较差。切比雪夫滤波器是在通带或阻带上频率响应幅度等波纹波动的滤波器,在过渡带上衰减快,和理想滤波器的频率响应曲线之间的误差最小,该滤波器在通带和阻带的误差均匀分布,因此其频率响应显示出等波纹性,阶次可以比较低。因此,切比雪夫等波纹逼近滤波器可以有效地滤除语音信号的噪声。切比雪夫滤波器的振幅平方函数为:

式中Ωc为通带截止频率,ε为与通带波纹有关的参量,为N阶切比雪夫多项式,定义如公式(3):

1.3 三电平削波
检测音乐信号的自相关函数峰值的位置就可以提取出信号的基音周期,进而计算音乐信号的基音频率[3]。但是由于自相关函数有许多峰值,而检测到的峰值可能会偏离其真实位置,造成误检,同时由于自相关函数的计算中有大量的乘法运算,因此首先对信号进行“三电平中心削波”处理,其削波函数为:

式中,x(n)为输入信号,y(n)为三电平中心削波的输出信号,CL为削波电平,它是音乐信号段内最大幅度值的一个百分比分数。音乐信号的基音信息大量存在于信号的高幅部分,削波不会影响信号基音频率的提取。削波后的信号值只有-1,0,1这3种情况,因而不需要做大量复杂的乘法运算,保证了音频信号处理的实时性和高效性。中心削波器如图2所示。
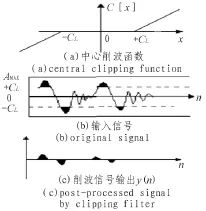
图2 信号削波处理Fig.2 Processing of clipping the signal
1.4 自相关处理
一般认为音频信号在短时内是平稳的,具有周期性,因此信号的自相关函数也具有周期性。信号的自相关函数会在周期的整数倍上出现峰值,检测出峰值的位置就可以提取信号的基音周期,进而计算信号的基音频率。信号的自相关函数定义式如下:
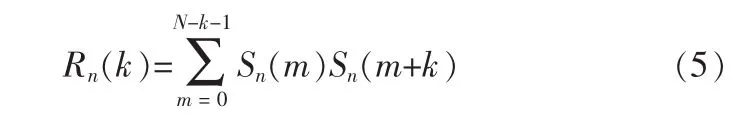
其中,N为采样点总数,Sn(m)为经过预处理短时加窗后的音频信号,RN(k)为 Sn(m)的自相关函数,且为偶函数,k 的取值范围为(-N+1)~(N-1)。
1.5 谐波干扰排除处理
当RN(k)为最大值时的位置就是基音周期,虽然经过一次三电平中心削波处理,但是还有可能存在谐波峰值的干扰,当RN(k)取得最大值时的k值有可能是高次谐波的周期,这样就会将谐波频率误认为基音频率,导致对音乐信号基因周期的错误识别。为了进一步消除高次谐波的对自相关峰值提取的干扰,对第一次自相关输出再进行一次三电平削波处理,并再次计算其自相关函数RN(K)′,因为在短时内音频信号具有周期性,RN(k)的周期与信号的基音周期相同,而RN(K)′是 RN(k)的自相关函数,因此,RN(k′)′与音乐信号的基音周期也相同。所以,只要找到RN(k′)′最大值时的位置,就可以更准确地提取出信号的基音周期。信号的基音频率可以由信号的采样频率和信号自相关函数峰值的位置计算得出。
2 实验结果分析
实验通过matlab编程实现音乐信号读取和分析处理。首先采用带通滤波器对音乐信号中的80 Hz~3 400 Hz频率段提取,然后采用本文提取的方法进行实验分析验证。
图3给出了切比雪夫滤波器对含有噪声的音乐信号进行滤波前后的波形结果比较分析,噪声信号添加的是高斯白噪声,从结果中清晰看到切比雪夫滤波器可以有效地滤除噪声信号。
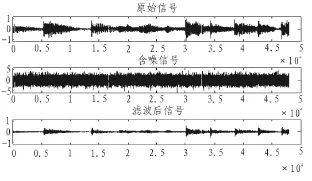
图3 切比雪夫滤波器对信号滤波Fig.3 Chebyshev filter for signal filtering
对算法的稳定性进行的验证,并做了详细比较,利用中值平滑处理算法消除基音周期的“野点”,并通过采样频率和信号自相关函数峰值的位置来计算基音的周期,图4的峰值即为此段信号的计算得到基音周期,峰值的大小范围为2.5~9.8 ms,所以此段内音乐信号的基音频率范围为102~400 Hz,从图4(c)误差分析结果中可以看到本文提出的算法对噪声有很好的抑制作用,并没有因为噪声的影响,而得到结果偏差,最大误差绝对值控制在0.6以内。

图4 计算基音周期Fig.4 Calculated pitch period
3 结 论
本文对音乐信号基音频率的提取采用自相关函数法,利用切比雪夫滤波器滤除环境噪声得到较为纯净的音乐信号,采用三电平中心削波法减少自相关处理计算量,提高了检测的实时性,两次三电平中心削波和自相关处理可以有效地抑制高次谐波的干扰。并测试该算法对噪声的抑制作用,实验结果证明本文提出的方法可以准确、稳定的提取音乐基音频率。
[1]Rabiner L R,Cheng M J,Rosenberg A E,et al.A comparative performance study of several pitch detection algorithms[J].IEEE Trans on Acoustics,Speech,and Signal Processing,1976,24(5):399-418.
[2]Rossm J,Shaffer H L,Cohen A,et al.Average magnitude difference function pitch extractor[J].IEEE Trans on Acous-tics,Speech,and Signal Processing,1974,22(5):353-362.
[3]赵力.语音信号处理[M].北京:机械工业出版社,2003:38-40.
[4]LI Ru-wei,BAO Chang-chun,DOU Hui-jing.Pitch detection method for noisy speed signals based on pre-filter and weghted wavelet conefficiens[C]//Proc.of the 9th International Conference on SignalProcessing:Beijing,China: [s.n.],2008:530-533.
[5]Kunieda N.Pitch extraction by using autocorrelation function on the log spectrum[J].Electronics and Communications in Japan Part Iii-Fundamental Electronic Science,2000 (83):90-98.
[6]Wang Y.A new pitch detection algorithm based on RCAF[J].2009 WRI World Congress on Computer Science and Information Engineering,2009:126-130.
[7]Heckmann M,Joublin F.Pitch extraction in Human-Robot interaction[C]//Intelligent Robots and Systems (IROS),2010 IEEE/RSJ International Conference on.Taipei,China:[s.n.]2010:1482-1487.
[8]Li M Y,Li T.Pitch recognition based on intelligent neural network system[J].2004 International Conference on Communication,Circuits,and Systems,2004,1(2):1081-1085.
