f+v分解与分形图像修复算法设计

白宗文，张威虎，周美丽

（延安大学 物理与电子信息学院，陕西 延安 716000）

数字图像修复是指用一定的算法来对指定区域缺损数据进行填充的过程，包括受损图像恢复，剔除或者取代图像中指定部分，达到图像复原或者接近原图像的视觉效果。本文提出的修复模型首先需要对图象进行分解，将其分解成纹理部分和结构部分，结构部分采用文献[1]提出的CDD模型进行修复，纹理部分以分形维度作为相似度度量函数进行修复，达到了很好的修复效果。

1 图像分解

文献[2]给出了一种图像分解方法。图像分解有两个关键要素，第一是针对图像噪声和恢复的整体变分最小化，第二是描述纹理或者噪声的空间振荡函数。

设 I：R2→IR 是一幅给定的目标图像，I∈L2（R2）。 I是包含图像u或者是一幅纹理图像，则u是图像I简单近似图像。

引入另外一个函数v，u和I的关系由简单线性模型表示成：

I（x，y）=u（x，y）+v（x，y）

从图像I重构u的问题其实是按照如下关系，对一个空间有界变分函数BV（R2）最小化

其中λ＞0是一个调节参数，能量的第二项是保真项，而第一项是调节项，用来去除噪声或者一些细节，而保持重要特征或者尖锐边缘。

文献[3]证明了当λ较小时，模型将消除图像中的纹理。为了能够从图像I中提取出u∈BV和v作为振荡函数，Meyer提出使用不同的空间函数，在某种程度上说是双BV空间。他引入了以下定义。

定义1：设G表示构成所有通用函数 v（x，y）属于 Banach空间，其可以写成

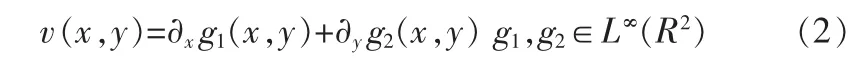
文献[3]Meyer指出：如果v分量表示纹理或者噪声，则v∈G，并给出了如下图像恢复模型inf{E（u）=

这种模型可以用于结构和纹理分解。下面是一种最小化方法：

其中λ，u＞0是可调参数，并且p→∞，第一项确保u∈BV（R2），第二项保证满足 I≈u+div（g1， g2），第三项是 G 的范式v=div（g1， g2）。 当 p→∞，λ→∞，则就是 Meyer提出的模型。

令0＜p＜10，实验结果表明效果非常接近。然而p=1时，计算速度快，所以这里令p=1，则可以给出欧拉-拉格朗日方程形式为：

根据以上模型，可以从一幅给定的纹理图像I中分离出分量 v 和分量 u。 这里 u 是图像的近似骨架（结构），v=div（g1，g2）表示图像的纹理或者噪声。

2 图像结构部分修复

按照以上算法将图像分解成了结构部分和纹理部分，根据各部分图像的不同特征，对于结构部分采用CDD（Curvature-Drive Diffusions），这是一种典型基于PDE的修复模型[1]，是对TV模型的一种改进，主要是为了克服TV模型中的视觉不连续问题，由于这种模型传导系数系数依赖于曲率，因此我们称之为曲率驱动扩散。在文献 [1]给出的TV模型当中，扩散强度仅依赖等照度的对比度和强度，这反映在传导系数的表达式

因此，传输强度并不依赖于等照度线强度的几何信息。对于平面曲线，其几何特性通过曲率尺度反映。

这样，当等照度线具有更大曲率的时候得到的扩散更强，当等照度线伸出的时候扩散自然消失。当选择 g（∞）=∞则扩散过于强烈，选择 g（0）=0 则扩散过弱，如果 g（0）≠a≠0。则CDD模型退化成TV模型修复的二阶方程。这样又可能出现不连通。因此，需要通过实验来确定该值的选择。

于是，令

像素点X处的曲率k是由该点的等照度线的曲率可以由下式给定

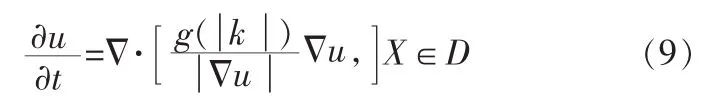
u=u0，X∈λ，其他

这里修复域D从数学上理解为开集，并不包含其边界，u0为图像的已知部分。当求解时域匹配方程时，则初始条件可以是任何合理猜测，也就是任意 u（X，0）只要满足 u（X，0）=u0（X），x∈Ω∈即可。

因此，CDD等照度修复模型又可以表示成

因为其和梯度相反所以是稳定的，可以将图像函数u看作某种特定粒子的强度函数。原始图像的已知部分可看作通过边界条件约束的恒定场源。

大多数情况下，原始图像的已知部分u0是含有噪声的，因为噪声将会通过边界进入修复区域，所以CDD修复方案对噪声很敏感。为了保证CDD修复效果，需要对图像做降噪处理。而本文采用经分解后，结构部分相当于已经进行了降噪处理。曲率驱动扩散的流动场为：

3 纹理部分修复

对于纹理图像经常采用纹理合成的方法进行修复，但目前没有很好的相似性度量函数，大部分采用的是颜色平方差的和（sum of squared difference，简称 SSD），该度量函数不符合人的视觉特性。纹理是物体表面不规则程度的一种度量，而图像的分形维数正好反映这种变化，它与人类视觉系统对图像纹理粗度的感知是一致的，因此本文提出一种以分形维度作为相似性度量函数的方法，用来实现纹理部分修复。

修复顺序是本算法的关键，文献[5]基于等照度线和样本的方法，对边界点进行优先级计算。给定一个点p∈∂Ω，定义p的优先级 P（p）=c（p）D（p）， 并有

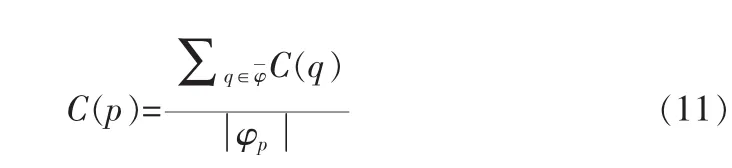
本文在纹理匹配时根据图像修复得到分形维度（FD）。对于Ψp中的每一个未知像素，以图像修复的结果作为它的已知值，并与Ψq（Pq∈Ψq，q∈I-Ω，Ψq中的每一个点为已知）中的点进行比较， FD（Ψp，Ψq）=FP-Fq（∀p∈φp，∀p∈φq）。 寻找与Ψp间最小的FD，Ψq对Ψp进行纹理填充。

4 数值分析

对于（2）式求解，设迭代的初始条件为：u0=f，g01=

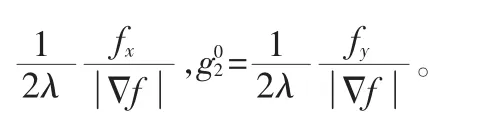
令 ui，j=u（ih，jh）， fi，j=f（ih，jh），g1，i，j=g1（ih，jh），g2，i，j=g2（ih，jh），其中 h＞0，表示步长，（ih，jh），表示离散点。 对于 0≤i，j≤M，为了能够简单的表示， 引入记号 H由以上符号定义，可以将离散的方程表示如下：

经推导最终可得

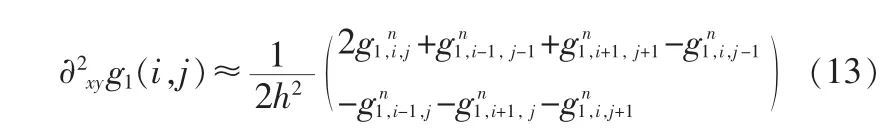
通过（13）式可以计算出分量u和v，参数选择如下，通常h=1，迭代次数 n=100，p=1。

对（7）式的求解采用中心差分法，以下迭代算法如下：

其中 Δt为时间步长，（n）表示在 nΔt的采样，接下来进行时域离散化。

随着时间步长的增长，图像函数u能够稳定的收敛于最终的结果。通常用来解决大尺度图像。因此有必要研究如何提高速度。

本文采用了的一项简单的技术就是在使用CDD时间匹配的开始就用一个好的初始值u（u，0）。首先运行TV模型，其输出结果作为好的初始猜测馈入到CDD修复过程中。由于TV修复模型是二阶的，时间匹配步骤可以比三阶的CDD更大，输出收敛更快。对于TV修复模型，除了时间匹配方法，Chan和Shen通过线性化和放宽技术也直接解出其稳态方程解。

分形维度计算采用文献[6]给出的公式：

5 结 论

本节给出采用本文提出的先分解成结构和纹理，然后分别采用BSCB修复模型和以形维度的相似度数的纹理部分修复，图1中（a）为原始图像，图像分解时参数选择为：h=1，迭代次数 n=100，p=1，（b）和（c）分别表示受损图像的结构部分和分，实验表明这种方法实现分解效果明显，所得（c）的纹理图像纹理性非常明显，接近标准性纹理。采用BSCB算法修复结构部分迭代次数 n=100，结果如（d）所示。（e）是以分形维度作为相似度度量函数的修复结果，图（f）表示f=u+v，即合成结果。

图1 图像修复Fig.1 Image restoration

[1]Chan T F，Shen J H.Non-texture inpainting by curaturedriven diffusions[J].Journal of Vision communication and Image Representation，2001，12（4）：436-449.

[2]Luminita A V，Osher S J.Modeling textures with total variation minimization and oscillating patterns in image processing[J].Journal of Scientific Computing，2003，19 （1）：553-572.

[3]Meyer Y.Oscillating patterns in image processing and nolinear evolutionequations[D].AMSuniversityLectureSeries，2002.

[4]Potlapalli H，Luo R C.Fractal-based classification of natural textures[J].IEEE transanctions on Industrial Electronics，1998，45（1）：142-150.

[5]Cisi A，Perez P，Toyama K.Object removal by exemplarbased inpainting[C]//Proceedings of Euro，2003.

[6]冯志刚，周宏伟.图像的分形维数计算方法及其应用[J].江苏理工大学学报，2001，22（6）：92-96.FENG Zhi-gang，ZHOU Hong-wei.Compute method and appliactiong of image fractal demension[J].Journal of Jiangsu University of Science and Technology， 2001，22（6）：92-96.