基于量子粒子群优化的最优障碍路径分析

刘亚威，张雪萍，杨腾飞

（河南工业大学 信息科学与工程学院，河南 郑州 450001）

最优路径分析是遥感和地理信息系统空间分析的重要技术之一，也是当前计算机科学领域中具有较高研究价值的一类问题。最优路径分析[1]问题源于计算机几何学的传统研究课题，此类问题可以描述为已知起始点、目标点以及环境信息，确定一条从起始点到目标点的与障碍物无碰撞的线路。目前考虑实际障碍物的最优路径分析方法有：可视图法、Dijkstra算法、A算法、栅格法、存在障碍物约束的最优控制法等。其中基于栅格法的最优路径分析具有数据结构简单、无需建立复杂的拓扑关系和进行复杂的拓扑运算以及处理速度快等特点，已成为目前研究最广泛的最优路径分析方法之一。

粒子群优化算法[2-4]最早是由Kenney博士与Eberhart博士于1995年提出的，源于对鸟群觅食的行为研究的PSO同遗传算法类似，它也是从随机解出发，通过迭代寻找最优解，通过适应值函数来评价解的品质。由于粒子群算法具有全局搜索能力不强，容易陷入局部最优的缺点，而量子粒子群优化[5]算法具有参数少，收敛速度快，鲁棒性好，能够较好地收敛于全局最优点等优点，能够很容易解决经典PSO算法中的不足，所以就用量子粒子群优化算法来取代经典的粒子群算法。

本文用栅格法建立环境模型，以量子粒子群优化算法作为基本的演化算法，将量子粒子群优化算法运用到栅格中，搜索出一条全局的最优路径，最后进行仿真实验，证明取得了很好的效果。

1 栅格空间建模

本文使用栅格法进行空间建模。栅格法[6-7]是把自由空间划分成一个由简单单元所构成的N×M的栅格阵，每一个单元就称为一个栅格，并且空间环境中障碍物的位置和大小都不发生变化。单元的划分可以是依赖于障碍物，也可以是独立于障碍物。对于独立于障碍物的单元分解，自由空间被划分成一些有规则形状的单元，同时测试每个单元是否属于自由位姿空间。由于单元的形状和位置独立于障碍物的形状和位置，所以这种方法并不一定能精确地表示障碍物。不过这种表示的误差可以通过增加单元的数量，即提高划分精度的办法来解决。

假设该空间为一个二维平面上的凸多边形有限区域，该区域内分布着有限个大小不同的静态障碍物，用尺寸相同的栅格对空间环境进行划分，并在该区域内建立直角坐标系。如果障碍区域为不规则形状，可以将其补为规则的正方形或者长方形或者其他形状，即让每个障碍物占一个或多个栅格，若障碍物不满一个栅格，则把此栅格补满，使其按一个栅格计算。在该区域建立的坐标系中，每个栅格都有对应的坐标和序列号，而且序列号和坐标一一对应。坐标（xp，yp）与序列号p之间的映射关系可以由公式（1）确定：

其中：int为取整运算，mod为求余运算，m为每一行的栅格数。

栅格法把工作空间分割成规则而均匀的含二值信息的栅格，用0和1分别表示自由栅格和障碍栅格。若某一栅格内不含任何障碍物，则称其为自由栅格；反之，则称其为障碍栅格。以20×20为例，划分后的数据空间如图1所示，其中图中阴影区表示障碍栅格，栅格中的数字表示序列号。

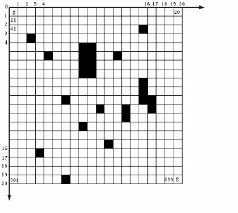
图1 直角坐标法建立的栅格Fig.1 Establishing grid by method of direct coordinate

我们的任务就是搜索一条由起点S到终点E的路径长度最短的避障路径。其目标函数可表示为：

其中：（xi，yi）为路径点的坐标信息，np为路径点的个数。

2 量子粒子群优化最优障碍路径分析

在粒子群优化算法中，粒子的运动状态由位置和速度描述，随着时间的演化，粒子的运动轨迹是既定的，同时粒子的速度受到一定限制，使得粒子的搜索空间是一个有限的区域，不能覆盖整个可行空间，从而PSO算法不能保证全局收敛，这个结论已经被Van de Bergh所证明。针对PSO算法的这个主要缺陷，根据粒子群的基本收敛性质，受到量子物理基本理论的启发，提出了量子行为粒子群优化[8-11]（Quantumbehaved Particle Swarm Optimization，QPSO）算法。

QPSO的量子系统是态叠加原理作用的一个复杂的非线性系统，所以一个量子系统比一个线性系统能描述更多的状态。量子系统与经典随机系统不同，是一个不确定性系统。在测量之前，由于没有既定的轨道，粒子在这样一个系统中会以一定的概率出现在任何位置。在传统PSO算法中，粒子必须在束缚状态以保证粒子群的聚集性，使PSO算法收敛到最优解或次优解。所以在传统PSO算法中，束缚状态限制了粒子在一个有限的区域中，而在QPSO优化算法中，有概率密度函数描述的束缚状态的一个粒子可以以一定的概率出现在整个可行搜索空间的任何位置，因此，其全局搜索性能远远好于一般PSO算法。

利用QPSO算法解决优化问题的两个重要步骤是：问题解的编码和适应度函数的选择。

在QPSO系统中，每个粒子个体代表一条从起点到终点的路径，如 xi=（xi1，xi2，…xiD），其中 D 表示粒子的维数大小，粒子的每一维都代表一个栅格序号，粒子的第一维表示起点栅格序号，最后一维表示终点栅格序号，将序号按照由小到大的顺序连接起来可构成一条路径。例如，从起点栅格序号1到终点栅格序号400的一条路径可以表示为：

1→21→147 →148→295→315→377→378→400

粒子编码可以表示为：

xi=（1，21，147，295，315，377，378，400）

适应值函数是量子粒子群算法中的一个很重要的因素，适当的选择适应值函数可以保证获得最小距离。以路径长度最短作为评价标准，选择适应值函数为：

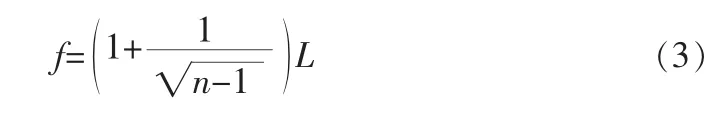
其中：n表示路径通过的栅格的数目，L为代表该路径的个体中相邻序号间直线距离之和，即式（1）。

量子行为粒子群优化算法的主要计算步骤如下：

Step1：初始化，设定最大进化代数maxT，将当前进化代数置t=1，在问题空间随机产生 M个粒子x1，x2，…，xm组成初始种群 X（t）；

Step2：计算所有粒子的平均最好位置：

Step3：评价种群X（t），计算每个粒子在每一维空间的适应值；

Step4：比较粒子的适应值和自身最优值pbest，如果当前值比 pbest更优，则置 pbest为当前值，即 if f（xi）＜f（pi），then xi=pi；

Step5：比较粒子的适应值和种群最优值gbest，如果当前值比gbest更优，则置gbest为当前粒子的适应值，即：

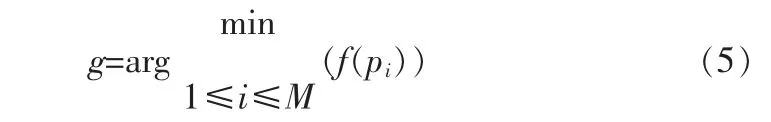
Step6：计算学习倾向点pd，对粒子的每一维，在 pid和 pgd之间得到一个随机点：

Step7：刷新位置：

Step8：检查结束条件（通常设为足够好的适应值或达到一个预设最大迭代数），若满足，则寻优结束；否则转至Step2。

在上述算法的公式（4）、（5）、（6）、（7）中：M 为种群中粒子的数目，D为粒子的维数，u和φ是在[0，1]上均匀分布的随机数，mbest是种群中所有粒子的平均最好位置点。和标准PSO一样，pid和pgd分别表示粒子所经历的最好位置和种群中所有粒子所经历的最好位置。β称为收缩扩张系数，是QPSO优化算法中惟一的参数，一般 β=（1-0.5）×（MaxT-T）/MaxT+0.5。

3 实验结果及分析

为了验证算法的正确性和可行性，对本文提出的算法进行了30次仿真实验，其中量子粒子群优化算法的参数设置如下：粒子个数M=30，最大迭代次数T=50，β从搜索开始的1.0线性递减到搜索结束的0.5。以图1所示环境为仿真实验的工作空间，假定工作空间在20×20的栅格环境中进行，栅格序号1为最优路径分析的起点，栅格序号400为最优路径分析的终点，实验结果如图2所示。

图2 QPSO算法计算机仿真结果Fig.2 The computer simulation result based on QPSO algorithm

图2中所示曲线即为搜索到的工作空间中的全局最优路径，从起点栅格序号1到终点栅格序号400的路径为：

1→22→62→167→168→210→211→316→336→399→400

粒子编码可以表示为：

xi=（1，22，62，167，168，210，211，316，336，399，400）

在图2所示环境下运行所得的平均最短路径长度为30.1，平均运行时间为26.4 s。在文献[12]中，用粒子群算法进行了30次仿真实验，粒子群的参数分别为：粒子数目Np=30，最大迭代次数Mp=50，c1=c2=2，初始惯性权重w由0.9随迭代次数线性递减到0.4，最大速度VMax=10。仿真结果如下图3所示。

在该仿真实验中，粒子群算法的空间障碍距离分析算法能以很快的速度收敛，但得到的障碍路径并不是全局最优路径，该方法不能有效的避免跨障碍问题。起始节点S点到目标节点E之间的路径是无效的，计算得到的障碍距离也是不具有实际意义的。

图2、图3仿真结果表明，量子粒子群算法能够解决粒子群算法中跨障碍的问题，并且能够以比粒子群算法更快的速度收敛，得到障碍环境下的全局最优路径。从以上结论可知在静态环境下，本文所提出的算法是有效且可行的。

图3 PSO算法计算机仿真结果Fig.3 The computer simulation result based on PSO algorithm

4 结 论

本文针对障碍环境下空间最优路径分析问题，提出了一种基于量子粒子群优化的空间最优路径分析方法。该方法以栅格法为空间环境建模，然后运用量子粒子群优化算法在环境中搜索全局最优路径。最后仿真实验证明该方法不仅可以找到最优路径，而且该方法具有建模容易，算法过程简单，易于实现，收敛速度快，参数少，能够较好地收敛于全局最优点等优点，完全可以用于空间全局最优路径分析问题，为带障碍空间路径分析问题的研究提出了一种新的思路。

[1]刘学锋，孟令奎，李少华，等.基于栅格GIS的最优路径分析及其应用[J].测绘通报，2004（6）:43-45.LIU Xue-feng， MENG Ling-kui， LI Shao-hua， et al.The optimal path analysis and it’s application based on grid GIS[J].Bulletin of Surveying and Mapping， 2004（6）:43-45.

[2]刘静，须文波.粒子群优化算法研究及其在优化理论中的应用[D].无锡：江南大学，2007.

[3]谭冠政，刘关俊.基于粒子群算法的移动机器人全局最优路径规划[J].计算机应用研究， 2007，24（11）:210-212.TAN Guan-zheng，LIU Guan-jun.The mobile robot global optimal path planning based on particle swarm optimization algorithm[J].Application Research of Computer， 2007，24（11）:210-212.

[4]Kennedy J，Eberhart R.Particle swarm optimization[C]//In：Proc of IEEE Int.Conf.on Neutral Networks， Perth，Australian，1995:1942-1948.

[5]高尚，杨静宇.群智能算法及其应用[M].北京:中国水利水电出版社，2006.

[6]高伟，张剑波.基于栅格数据模型的最优路径分析算法及实现[J].黑龙江工程学院报:自然科学版，2004，18（1）:22-24.GAOWei，ZHANG Jian-bo.Theoptimalpathanalysisalgorithm and implementation based on grid data model[J].Journal of Heilongjiang Institute of Technology:Natural Science，2004，18（1）:22-24.

[7]邓高峰，张雪萍，刘彦萍.一种障碍环境下机器人路径规划的蚁群粒子群算法[J].控制理论与应用，2009，26（8）：879-883.DENG Gao-feng， ZHANG Xue-ping， LIU Yan-ping.Ant colony optimization and particle swarm optimization for robot-path planning in obstacle environment[J].Control Theory and Applications， 2009，26（8）：879-883.

[8]唐槐璐，须文波.基于量子行为微粒群优化算法的数据聚类[D].无锡：江南大学，2008.

[9]Sun J， Feng B， Xu W B.Particle swam optimization with particles having quantum behavior[C]//IEEE Congress on Evolutionary Computation，2004：325-331.

[10]Sun J， Xu W B， Feng B.A global search strategy of quantum-behaved particle swam optimization [C]//IEEE Conference on Cybernetics and Intelligent Systems，2004：111-116.

[11]Sun J， Lai C H， XU Wen-bo.Quantum-behaved particle swarm optimization and its application [J].Journal of Computer and Mathematics with Applications，U.K.2005（49）：1669-1678.

[12]邓高峰，张雪萍.基于粒子群优化的带障碍约束空间聚类分析研究[D].郑州：河南工业大学，2008.