太子河闸坝河段水环境容量研究

诸葛亦斯，彭文启，杜 强，谭红武

（中国水利水电科学研究院 水环境研究所，北京 100038）

1 研究背景

闸坝的修建和调度是为满足人类对河流的多目标利用，对河流径流过程进行调控的有效途径。由于闸坝河流水文状况特殊，对闸坝的水流水质作用规律研究不足，闸坝河流的水环境容量计算方法一直存在争论［1］。有学者认为，出于合理性考虑，应分别对开闸期和关闸期的河流采用不同方法计算其容量并加和［2］；也有学者认为［3］，应考虑河道水体体积变化和污染物浓度沿程变化，采用改进的单箱水质模型计算其容量；目前实际操作中往往采用简单的零维或一维模型计算。为了充分发挥闸坝调度的优势以利用水环境容量这种特殊的资源，根据各河段调控后水文特征核定各河段水体的环境容量，逐步实现由指令型总量向容量型总量转变，闸坝调控水体的水环境容量优化配置研究亟待深入［4］。

太子河是辽河水系主要河流，流贯本溪境内，全河长464km，流域面积1.39万km2，年平均径流26.86亿m3。作为我国重要的工业基地，流域多行业多重污染的特点显著，水污染问题突出；流域内水库总库容大于地表水资源量，大中型水库工程与其它拦河坝、翻板闸联合使用，基本上控制了整个河流系统，流域水资源具有很大的可调控性，进而在一定程度上可调节河流水环境容量的大小。

本文将结合当地的社会经济、自然地理条件、水利工程、排污口设置和水功能区情况，模拟太子河水流条件和其中污染物迁移转化状况，在此基础上利用优化分配模型确定各个排污口的污染物的允许排放量，进而计算太子河闸坝河段的水环境容量。

2 太子河水量水质模型建立

有文献建议［5-6］，计算水环境容量时水面平均宽度超过300m的河流应采用二维模型计算，平均河宽小于此值的河流，应采用一维或者零维模型计算。如本应采用二维模型计算容量的水体，却误用一维或者零维模型计算，容量值被严重高估，结果不利于水环境管理［7］。太子河研究河段实际应用中，该河段平均宽度小于300m，应采用一维水流水质模型进行计算。

2.1 闸坝水量调控模型 本文研究区域中的闸坝类型包括大坝、拦河堰和水力翻板闸三类，空间分布如图1所示。在一维模型中，坝、堰和闸作为流量计算节点，其水力学特征需作特殊处理。其中大坝按水库实际调控的泄流量作为计算节点的流量；拦河堰属于堰流出流，在模型中采用堰流流量公式计算过堰流量

式中： ε为侧收缩系数；m为流量系数；B为过流宽度；H0为堰顶水头。

水力翻板闸的水量模拟具有一定难度，当闸体处于某特殊开度下该节点具有底部出流和顶部溢流的双重特征，在模型中采用下式计算过闸流量

式中：τ为协调系数；δ为压缩系数；w为闸门开启高度；y1、y2为闸上、下游水位；a、b为流量系数；α、β为闸门形态参数。

通过闸门的流量是闸门形状和上游水位的函数。对于给定闸门开度，流量依赖于压缩系数，压缩系数δ为：

式中：ys为维纳收缩点的高度。

根据堰坎厚度与堰顶水头之比以及水流特征将堰流分作薄壁堰、实用堰和宽顶堰三种。在实际工程计算中，根据堰流种类分别计算流量公式中的系数。

2.2 太子河干流入河排污口概化 由于研究流域范围内主要特点是工业发达，工厂较多，工业废水对河流污染起主要作用。所有污染源分别按子流域的归属，所有污染物最终汇入各条支流，通过支流汇入干流。干流入河排污口无法准确定位，且污染源数量多，故按照地域划分将干流排污口简化为太子河干流本溪排污口和辽阳排污口两处。概化后的入河排污口与水质控制断面的相对位置如图1所示，图1亦可见研究区域闸坝分布状况。

2.3 相邻闸坝的水量水质计算 相邻闸坝间的输入条件为开边界水文条件，水量水质关系具体计算公式如下：

式中：ΔVi为计算单元蓄水变化量，m3；Qi-1为闸坝上游流量，m3/s；qi-1为上游区间入流量，m3/s；Ri-1为上游支流、点源汇入量，m3/s；Ri为上游取用水量，m3/s；Qi为闸坝泄流量，m3/s；Δt为单位时间，s；Ci为闸坝下泄水质浓度，mg/L；Ci-1为闸坝上游水质浓度，mg/L；Cqi-1为支流、点源的水质浓度，mg/L；CRi-1为河段接纳的非点源污染浓度，mg/L；Vi为计算单元蓄水量，m3；Ki为计算单元污染物的综合降解系数，s-1。

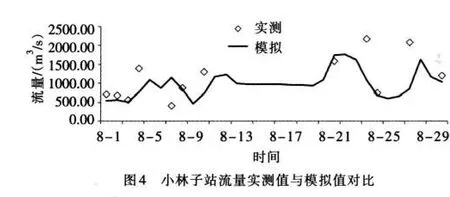
2.4 模型校核验证及参数确定 由于无法获取准确的入河排污口污染物排放过程，且河道沿程的非点源污染物的排入量也很难精确模拟，使得水质模型的精度无法得到保证。为尽量减少不确定因素的影响，课题组于2010年对太子河干流的本溪、辽阳、小林子和唐马寨4个站点进行了水质水量同步监测，以同步监测数据对水量水质模型进行校核验证，结果如图2—图7所示。模拟结果与实测值之间虽存在一定的误差，但由于研究区污染物排放的不确定性，其模拟精度已经可以满足水环境容量计算的需求。通过模型校核，将本文太子河干流河道内CODCr的衰减系数确定为0.15，水库和闸坝回水区内的CODCr的衰减系数确定为0.06。

3 太子河入河排污量优化分配模型

3.1 浓度传递系数矩阵 太子河研究区域按照水功能区划，不同水质控制断面的水质目标不同，控制断面的具体参数如表1所示，水质控制断面的空间相对位置如图1所示。基于水流水质模拟计算，可确定排污口逐一排放CODCr对各个水质控制断面水质的影响，即固定水流条件下入河排污口污染物浓度与各个控制断面污染物浓度的比例关系，表示浓度传递系数。

表1 水质控制断面参数

假定河道中水流为均匀流，第j个水质控制断面流量为Qj，平均流速为uj，污染物的综合降解系数为K，且上游排污口i污水排放量Qpi远小于河道流量，排污口i污染物排放对下游xij距离j断面浓度的影响可用浓度传递函数fij表示，其计算公式如下：

式中：Pi为第i排污口的污染物浓度，mg/L；Kij为第i排污口排放的污染物在第j控制断面造成的污染物浓度，mg/L；fij为第i个排污口污染物浓度在第j个控制断面造成的污染物浓度与第i排污口的污染物浓度之比，在水流条件不变情况下该比例关系不变；A为上述浓度比例关系汇总，即浓度传递系数矩阵。各个排污口逐一排放浓度为单位浓度的CODCr污染物，其他排污口无污染物排放情况下，相应各个水质控制断面的CODCr浓度传递系数如表2所示。

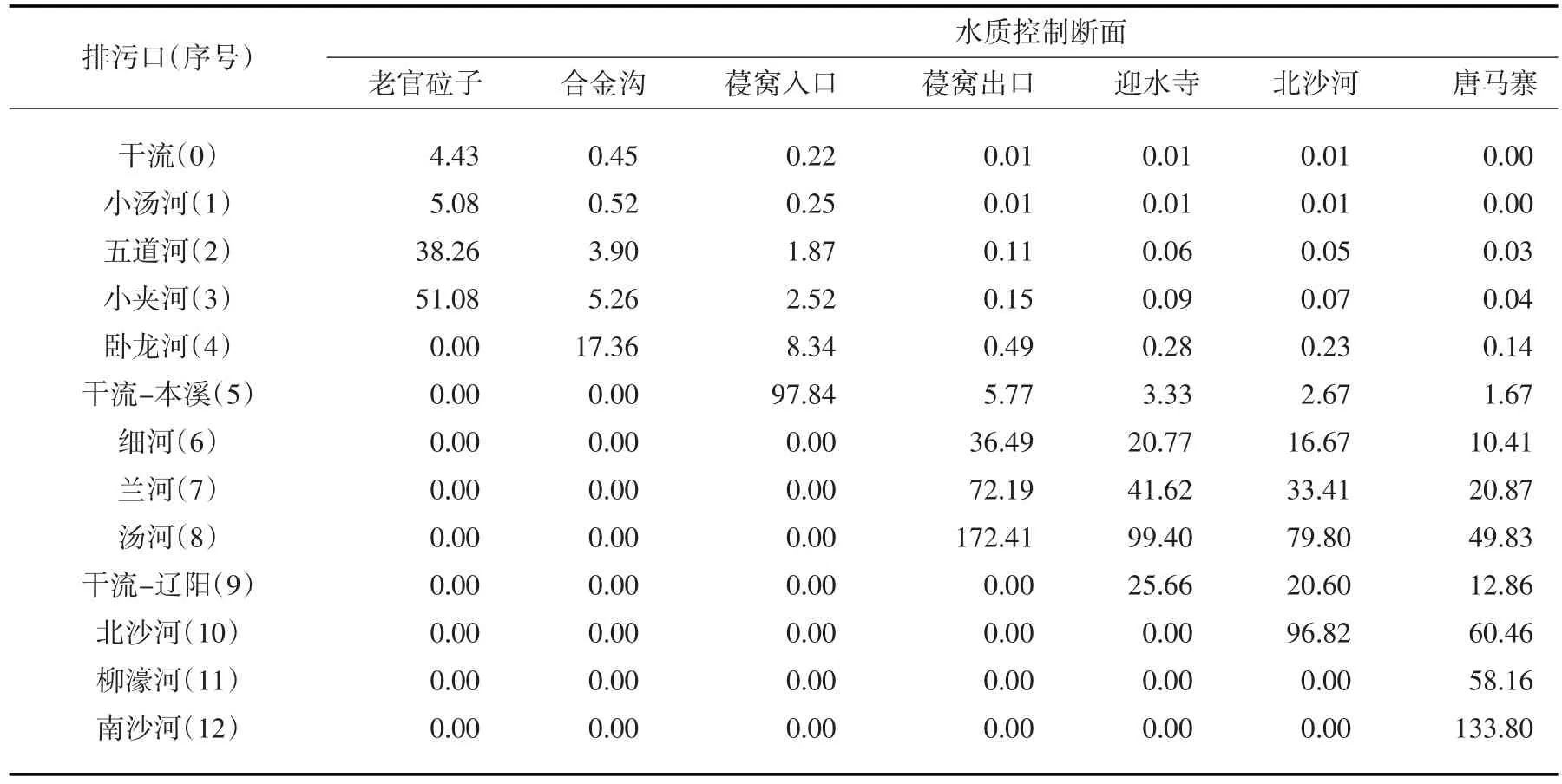
表2 太子河CODCr浓度传递系数矩阵 （×10-3）

3.2 优化分配模型目标及约束 太子河污染物排放分配目标可设定总削减量最小，即在满足水质断面水质要求的前提下，各排污分配方案中排污口排放量与现状污染物排放量总量变化最小，如下式所示

约束条件为各个水质控制断面水质必须达标，如下式所示

式中：ΔM 为污染物总消减量，t/a；n为排污口总数；Pi为i排污口的污染物浓度，mg/L；Qi为i排污口的污水排放量，m3/a；Di为i排污口的现状排放量，t/a；Kj为第j水质控制断面的污染物浓度，mg/L；为第j水质控制断面的水质目标，mg/L；m为水质控制断面数量，个。

3.3 分配模型求解方法 粒子群算法（Particle Swarm Optimization，简称PSO）是由Kennedy和Eberhart提出一种基于群体的演化算法，其思想来源于人工生命和演化计算理论。PSO初始化时产生随机粒子群即随机解，每一次迭代中每个粒子通过跟踪两个极值自我更新。一个极值是该粒子当前找到的最优解，称为个体极值点Pi，另一个极值是整个群体目前找到的最好解，称为全局极值点Pg。根据以上两个最优解，粒子根据式（8）和式（9）更新变化速度和当前值。设有m个粒子，粒子i的信息可用D维向量表示，当前值为Xi=（xi1，xi2，…，xiD），变化速度为Vi=（vi1，vi2，…，viD），个体极值点表示为Pi=（pi1，pi2，…，piD），群体极值点表示为Pg=（pg1，pg2，…，pgD）。则粒子的当前值和变化速度更新方程如下：

式中：wf为惯性因子，wf大则算法具有强的全局搜索能力，wf小则算法倾向于局部搜索，一般默认值0.4；c1、c2为学习因子，通常取［1，2］间常数；rand是［0，1］内随机数；Pi为粒子当前局部最优值；Pg为当前群体最优值。

粒子不断调整变化速度和当前值时，还受最大速度vmax的限制。

4 考虑闸坝调控影响的水环境容量计算

水环境容量是特定水文条件下水体的自净能力的定量表征，可视为一种自然资源，容量总量控制正是把水环境容量作为一种自然资源其进行开发利用。由于闸坝调控影响河流水体的水力学条件，本文将该类特殊水体的总量控制按以下步骤进行确定：（1）根据当地的自然地理条件及水利工程特征，模拟水体稀释自净能力和污染物迁移转化规律；（2）根据水功能区确定控制断面水质目标；（3）根据当地经济、技术条件和排污口设置，结合优化分配模型确定污染物的允许排放量；（4）按照优化分配污染物负荷总量和应削减量，计算水环境容量；（5）根据水环境容量的分布实现工业的合理布局。

在太子河水量水质模型的基础上，考虑闸坝调控对水流状况的影响，基于污染物浓度传递矩阵，计算研究河段的水环境容量。目标总削减量最小即在满足水质断面水质要求的前提下，各排污分配方案中排污口排放量与现状污染物排放量总量变化最小。根据现状排污量计算现状断面水质状况及超标状况见表1。太子河各个排污口优化配置后的CODCr排放浓度、排污量以及与现状排污量的对比如表3所示。

表3 各排污口CODCr排放量分配 （单位：t）

表4 排放量分配后各水质控制断面CODCr浓度 （单位：mg/L）

经过优化配置后各排污口CODCr排放量总和较现状排放量有所减少，已保证各个水质控制断面水质达标，见表4。计算得到各个河段间的CODCr水环境容量分别为：老官砬子以上河段1173.5t/a，老官砬子至合金沟河段80.7t/a，合金沟至葠窝入口河段6714.3t/a，葠窝入口至葠窝出口河段8680.9t/a，葠窝出口至迎水寺河段1035.8t/a，迎水寺至北沙河河段4175.4t/a，北沙河至唐马寨河段8253.9t/a。

5 结论

本文构建了太子河闸坝河段水量水质模型和入河排污量优化分配模型，提出了满足水质控制断面水质要求且削减量最小的入河排污量分配方案，进而计算闸坝影响区域水体的水环境容量。辽宁太子河流域为东北老工业基地，全区工农业都比较发达，短期内根据水环境容量的优化调控实现工业的合理布局估计无法实现。但通过干流入河排污量的优化配置，尽量按要求削减污染物排放，提高研究区水质还是完全可行的。

［1］王华，逄勇，丁玲.滨江水体水环境容量计算研究［J］.环境科学学报，2007，27（12）：2067-2073.

［2］王军良，方志发.城中湖水环境容量计算和对策研究［J］.环境科学与技术，2008，31（1）：129-132.

［3］张永勇，夏军，等.淮河流域闸坝联合调度对河流水质影响分析［J］.武汉大学学报（工学版），2007，40（4）：31-35.

［4］Muñoz-Carpena R，Vellidis G，Shirmohammadi A，et al.Modeling tools for MDL development and implementa⁃tion［J］.Trans.ASABE，2006，49（4）：961-966.

［5］Zhang H X，Yu S L.Applying the First-Order Error Analysis in Determining the Margin of Safety for Total Maxi⁃mum Daily Load Computations［J］.Journal of Environmental Engineering，2004，130：664-673.

［6］叶碎高，郑世宗，刘红.山区性河道水环境容量及合理配置研究［J］.水利学报，2007，36（增刊）：573-576.

［7］左其亭，高洋洋.闸坝对重污染河流水质水量作用规律的分析与讨论［J］.资源科学，2010，32（2）：261-266.