常见电路的动态分析问题的解法实例

宋振全

(江苏省睢宁高级中学南校,江苏睢宁 221200)

电路的动态分析问题是历年高考选择题中必考的习题,这类问题着重考查的学生的应用基本知识分析问题的能力,具有很强的灵活性,学生做这些问题时易出错,下面笔者结合具体习题谈一谈这类问题的解法.

1 闭合电路的电压电流的动态变化分析

例1.如图 1所示的电路中,R1、R2、R3、R4皆为定值电阻,R5为可变电阻,电源的电动势为 E,内阻为r.设电流表A的示数为I,电压表V的示数为U,当滑动触头向上移动时

图1

(A)I变大,U变小.

(B)I变大,U变大.

(C)I变小,U变大.

(D)I变小,U变小.

解析:整个电路的连接形式为 R2、R4串联后与电阻R5并联,然后再与电阻 R1、R3串联接在电源上,电压表测量的是路端电压,电流表测量的是流过 R2、R4的电流,当滑动触头向上滑动时R5接入电路的阻值变小,R2、R4串联后再与 R5并联的这部分电阻减小,这部分电路再与R1、R3的串联的总电阻值也减小,即外电路的总阻值变小,所以,根据闭合电路欧姆定律,干路中的总电流增大,路端电压变小,所以电压表的示数应该变小,R2、R4两端的电压减小,电流表的示数应变小,所以正确的答案为(D).

方法归纳:(1)解题先明确电流表和电压表是测量哪一部分的电流和电压和各个电路元件的连接情况.(2)电路中无论各元件是串联、并联还是混连,只要其中任何一个电阻变大,总电阻就随之变大,反之总电阻变小.电路中如有开关控制的电路与此相似,若开关通断使串联的用电器增多则总电阻增大,若开关的通断使并联的用电器增多则总电阻减小.(3)这类问题的解题基本解题思路为“部分→整体→部分”,即从电阻的变化的部分入手,再由闭合电路欧姆定律判断 I总和U路端的变化情况,最后再判断部分电路的I和U变化情况.(4)根据滑动变阻器的阻值变化情况,可以用“串反并同”来判断变阻器并联的电路和变阻器串联的电路中的电流和电压的变化,“串反”即与变阻器串联的电流表或用电器中的电流变化与变阻器的阻值变化相反,也就是变阻器的阻值变大用电器的电流就变小,变阻器的阻值变小用电器的电流就变大.“并同”是指与变阻器并联的那部分电路中电压的变化和电流的变化和变阻器阻值的变化相同,即变阻器的阻值增大与变阻器并联的那部分电路的电流和电压都增大,反之亦然.

2 闭合电路中的电流和电压变化量的分析

例 2.(2006上海)在如图2所示的电路中,闭合开关S,当滑动变阻器的滑动触头 P向下滑动时,4个理想电表的示数都发生变化,电表的示数分别用 I、U1、U2和 U3表示,电表示数变化量的大小分别用ΔI、ΔU1、ΔU2、ΔU3表示.下列比值正确的是

图2

方法归纳:(1)讨论此类问题时涉及到变化量可以根据闭合电路欧姆定律将电路分为内电路和外电路.由于电动势是定值,所以内外电路的的电压变化量相同,即ΔU内=ΔU外.(2)可以将定值电阻等效地看成电源的内阻,处理习题会很方便,上题中我们如果将 R1和电源看成一个整体,这时电源的电动势为E,内阻就是R1+r.由此我们还知道U1减小,U2增大,但 U1减少量和 U2的增加量不相等,而是ΔU1＜ΔU2,具体一些说应该是ΔU2=ΔU1+ΔUr.

3 滑动变阻器连接所形成的对称电路问题

例3.如图 3所示,电源的电动势E=8 V.内阻不为零,电灯A标有10 V,10 W的字样,电灯B标有 8 V,20 W 的字样,滑动变阻器的总电阻为6 Ω.闭合开关 S,当滑动触头从上向下滑动的过程中(不考虑电灯电阻的变化)则

图3

(A)电流表的示数一直增大,电压表的示数一直减小.

(B)电流表的示数一直减小,电压表的示数一直增大.

(C)电流表的示数先增大后减小,电压表的示数先减小后增大.

(D)电流表的示数先减小后增大,电压表的示数先增大后减小.

解析:由图知 A灯、B灯、滑动变阻器组成的电路中,滑动变阻器分成两部分联入电路,设与 A灯连接的那部分电阻为RX,滑动变阻器的电阻为 R,这部分电路的有效电阻大小为

方法归纳:滑动变阻器分成两部分分别联入两个支路中时,当滑动触头滑动时,使两个支路的电阻分别相等时,这样的电路称为对称电路,这时电路中的总电阻最大.如上图,如果不能形成对称电路,则当两个支路的阻值越接近其总阻值越大,反之则越小.先由电阻的变化再判断其他物理量的变化.

4 电路的故障问题

例4.如图4所示的电路,闭合开关 S后,灯 L1、L2都能发光,后来由于某种故障使灯L2突然变亮(未烧坏),灯 L1变暗,电压表的读数增大,由此可推断,这故障可能是

(A)电阻 R1断路.

(B)电阻 R2短路.

(C)灯L1两接线柱间短路.

图4

(D)电阻 R2断路.

解析:由图知,电压表测路端电压,当其读数突然增大,据闭合电路欧姆定律知,外电路总电阻增大.同时灯L2变亮,说明L2两端的电压增大.所以故障一定是R2断路,正确答案为(D).

方法归纳:电路中某部分出现断路,因断路部分的电阻无穷大,可以理解为这部分电路的电阻增大,而且增至无穷大.电路中某部分出现短路,因短路部分的电阻接近零,所以可以认为这部分电阻减小,而且减小至零,这样就可以确定总电阻的变化.再结合闭合电路欧姆定律处理其他问题.

5 直流电路中接有电感线圈时,电路的通断所引起的动态变化分析

例5.(2008年江苏)如图5所示的电路中,3个相同的灯泡 a、b、c和电感L1、L2与直流电源连接,电感的电阻忽略不计.电键S从闭合状态突然断开时,下列判断正确的有

(A)a先变亮,然后逐渐变暗.

(B)b先变亮,然后逐渐变暗.

(C)c先变亮,然后逐渐变暗.

(D)b、c都逐渐变暗.

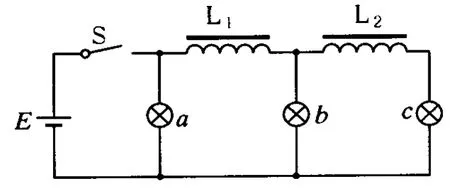
图5

解析:电路稳定工作时,由于电感的电阻不计,3灯泡中的电流相同,亮度一样.开关断开后,电路中的电流发生变化,但由于电感线圈发生自感作用,电路中的电流不会发生突变,而是渐变,即电流从原来的值缓慢地减小到零.若断开前每个灯泡中的电流为 I0,则图中电感L1中的电流I1=2I0,L2的电流I2=I0,所以断开后的瞬间灯b和灯c中的电流仍与断开前一样大小为I0,而灯 a的电流为2I0,然后他们逐渐地减小,所以本题选(A)、(D).

图6

方法归纳:(1)、自感现象通常情况下分为通电自感和断电自感,根据 LR电路的暂态过程的理论分析(见赵凯华、陈熙谋编著的《电磁学》),电路中的电流按指数规律变化,在图6中S打向1后,L中的电流变化规律为i=,当开关拨到2时,L中的电流变化规律为i,其电流随时间变化的图像如下图7和8所示.

图7

图8

(2)灯泡的变亮还是变暗取决于开关断开前后通过灯泡电流的变化情况,上题中开关断开前后瞬间b灯和c灯的电流一样,而a灯的电流加倍,所以a灯的亮暗变化情况和b、c两灯不一样.

6 接有电感和电容的的直流电路动态变化问题

例6.如图9所示电路中,L为电感线圈,C为电容器,当开关S由断开变为闭合时,则

图9

(A)A灯有电流通过,方向由a到b.

(B)A灯中无电流通过,不可能变亮.

(C)B灯立即熄灭,c点电势低于d点电势.

(D)B灯逐渐熄灭,c点电势低于d点电势.

解析:开关闭合前,电容器的支路中没有电流,但电容器被充电,两极板带上等量的异种电荷,且灯A不亮,电感线圈的电路有电流通过,灯泡发光.开关闭合时上述的两个支路被短路,所以就形成线圈 L→灯B→线圈L以及电容C→灯 A→电容 C的两个闭合回路.电感线圈发生自感,电容器放电,所以选(D).

方法归纳:(1)直流电路中,连接电容器的电路在电路稳定时相当于断路,但电容器两极板却带电.两极板间的电压等于和电容器的电路并联的那部分电路两端的电压,在充电和放电的瞬间,电路中存在瞬时电流.(2)电感线圈发生断电自感时,线圈相当于电源,电流流出的一端相当于电源的正极.

7 接有变压器的交流电路动态变化分析

例7.如图10所示,是变压器通过降压给用户供电的示意图.变压器输入电压是市电网的电压,不会波动,输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器的R表示用户用电器的总电阻,当滑动变阻器的触头向下移动时,下列说法中正确的是

(A)相当于在增加用电器的数目.

(B)V1表的示数随V2表的示数的增大而增大.

(C)A1表的示数随A2表的示数的增大而减少.

(D)变压器的输入功率在增大.

解析:选(A)、(D).因为用户的用电器都是并联的,并联的用电器越多,电路中的电阻越小.接入的用电器越多用户消耗的功率越大,理想变压器工作时输出功率和输入功率相同,所以选(A)、(D).

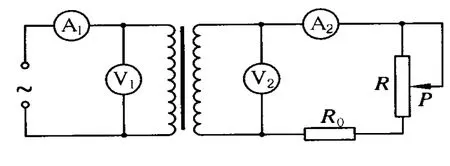
图10

8 交变电流电路中接有电感和电容的动态变化问题

例 8.如图 11 所示,交流电表 A1、A2、A3分别与电容器、线圈L和电阻R串联后接在同一个交流电源上,供电的瞬时电压值为 u1=Umsinω1t,3个电表各有不同的读数.现在换一个电源供电,供电电压的瞬时值为 u2=Umsinω2t,ω2=2ω1.改换电源后,3个电表的读数怎样变化?

图11

解析:A1表的示数不变,由电感线圈对交变电流的阻碍作用我们称之为感抗,其大小为 XL=2πfL=ω L,ω2=2ω1,阻碍作用变大,A2的示数变小,电容对交变电流阻碍作用,我们称之为容抗,其大小为,所以A3的示数变大.

方法归纳:电阻对交流电的阻碍作用与交流电的频率无关,电感线圈连接在电路中时,线圈对交变电流有“通低频,阻高频”的作用,交流电的频率越大,其对电流的阻碍作用越大.电容器对交变电流的作用是:“隔直流、通交流,阻低频、通高频”,交变电流的频率越大,电容器的阻碍作用就越小.

总之,对于电路的动态分析问题,我们只要把握这类问题的规律,从根本上找到这类问题的解决办法,一定会在高考中少犯错误.