未决赔款准备金评估的Mack模型及其预测均方误差的实现

张连增，段白鸽

（南开大学 经济学院，天津 300071）

1 Mack模型

1.1 Mack模型基本假设

传统的确定性链梯法是从累计赔款流量三角形出发估计未决赔款准备金的一种方法，该方法应用简便。在该方法下，可得到如表1的累计赔款流量三角形的一般结构。

表1 累计赔款流量三角形示例

在表1中，Ci,j表示事故年i到第j个进展年的累计赔款额（0≤i≤I,0≤j≤J）。另外一般假设I=J。

用 Ri表示对应于事故年 i的未决赔款准备金，R表示各事故年未决赔款准备金的总额。在传统链梯法中，下列关系式成立：

在应用链梯法时，首先要估计进展因子，其后估计未决赔款准备金，其基本步骤如下：

现在引入Mack模型。在Mack模型中，Ci,j都被视为随机变量。Mack(1993)[1]引入了以下两个基本假设：

（1）对不同的事故年i，Ci,j是相互独立的。

（2）对所有的 0≤i≤I，1≤j≤J，存在进展因子 f0,…,fJ-1＞0和,…,＞0 方差参数，使得：

对上述两个假设可解释如下：假设（1）表明，不同事故年的累计赔款额是相互独立的，因而是不相关的。假设（2）表明，不同事故年有相同的进展因子序列，而且链梯法应用最近的观察值来预测未来的赔款，即可以视为Markov链梯法。

1.2 Mack模型中估计量的无偏性

在上述假设下，可以证明（3）～（6）式给出的估计量分别是，fj，Ci,J,Ri和R的无偏估计量。同时，Mack(1993)给出了关于的如下估计：

下面首先证明在Mack模型的三个基本假设下，（3）～（6）式分别是 fj，Ci,J，Ri和 R 的无偏估计；其次证明在（8）式的假设下，是关于fj的最小方差的线性无偏估计；最后证明关于σj2的估计（9）式的无偏性。

1.2.1 （3）～（6）式估计量的无偏性

实际上，仅需证明下面两个定理就可以说明（3）～（6）式估计量的无偏性。

定理1 记所有已知的上三角数据集合为DI={Ci,j,i+j≤I}。 根据假设（1）和（2），E(Ci,J|DI)=Ci,I-ifI-i…fJ-1成立。

证明：记 Ei(X)=E(X|Ci,1，…,Ci,I-i)，根据假设（1），不同的事故年i,Ci,j的相互独立性，得到：

E(Ci,J|DI)=E(Ci,J|Ci,1,…,Ci,I-i)=Ei(Ci,J)

注意到再反复应用（7）式就可得到：

Ei(Ci,J)=Ei(E(Ci,J|Ci,1,…,Ci,J-1))

=Ei(Ci,J-1)fJ-1…=E1(Ci,I-i)fI-i…fJ-1=Ci,I-ifI-i…fJ-1

定理 2 在假设（1）及假设（2）下，{f^j,0≤j≤J-1}是无偏的，而且不同的进展因子之间是不相关的。

证明：记 Bj={Ci,k,k≤j,i+k≤I},0≤j≤J，根据假设（1）和假设（2），得到：

E(Ci,j+1|Bj)=E(Ci,j+1|Ci,1,…,Ci,j)=Ci,jfj

因此，可以得到：

设 k＜j，那么

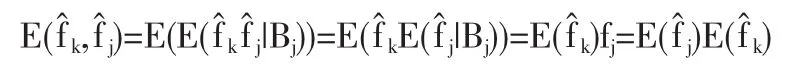
这就证明了定理2。

根据定理2，显然有：

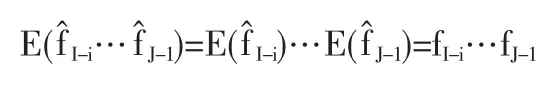
1.2.2 fj的最小方差的线性无偏估计

引理 设X1,…,Xn为相互独立的随机变量，且满足E(Xi)=μ，(1≤i≤n)要使在约束条件下，随机变量的线性组合的方差达到最小，那么，wi=c/Var(Xi)（1≤i≤n），其中 Var(X)=c。

证明：上述问题等价于确定以下多元函数的条件极值：

为此构造拉格朗日函数，求解下述方程组：

解方程组 (*)得到 wi=c/Var(Xi)（1≤i≤n）， 其中 c=

故使得方差达到最小的随机变量的线性组合为：进一步得出，

故引理得证。

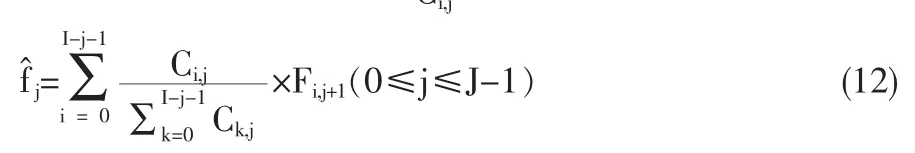
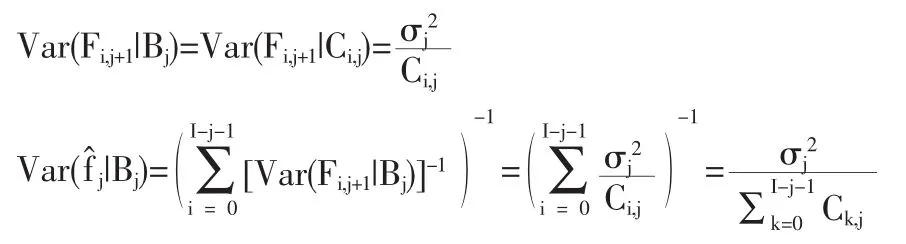
上式右边三项分别为：

将上述三项代人，得到：

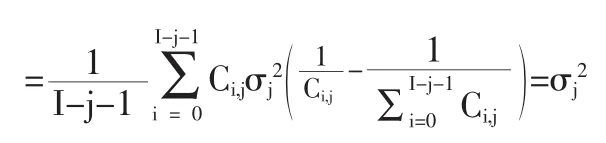
2 Mack模型中预测均方误差的计算

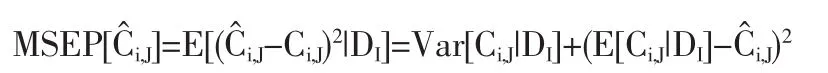
其中，Var[Ci,J|DI]表示纯粹的随机误差（即过程方差）[3]，上式最后一项表示估计值与期望值的偏差（即参数估计误差）。

预测均方误差定义为关于已知数据的条件期望而不是无条件期望E(C^i,J-Ci,J)2，这是因为建立在已知数据上的估计量C^i,J的条件预测均方误差，给出了C^i,J与Ci,J之间由于随机性引起的平均偏差，更具有研究价值。对于预测均方误差，下面的关系式成立：

2.1 条件过程方差

根据Mack模型假设（1）和假设（2），可以得到：

进一步，利用递推公式，得到条件过程方差：

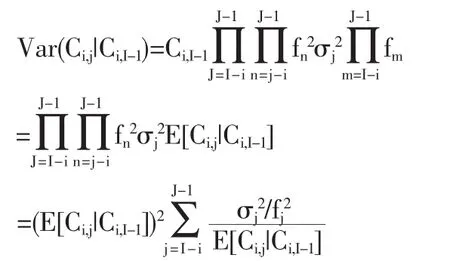
由Mack模型假设（1）得到，各事故年的未决赔款准备金之和的条件过程方差为：

把参数fj和分别替换为各自的估计量和可得到各事故年的条件过程方差的估计量，即为：

进而得到，各事故年的未决赔款准备金之和的条件过程方差的估计量为：

2.2 参数估计误差

根据Mack模型假设（1）和假设（2），可以得到条件参数误差：

在（16）式中，如果把fj简单地替换为，那么结果为零。因此，需要采用另外的方法来估计该项。为简便起见，引入符号：

将上式代人（16）式，得到：

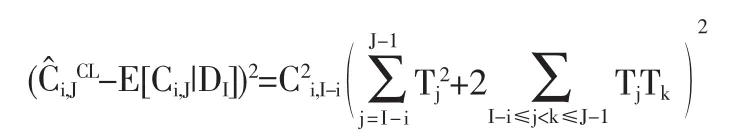
另外，因为：

从而得到：

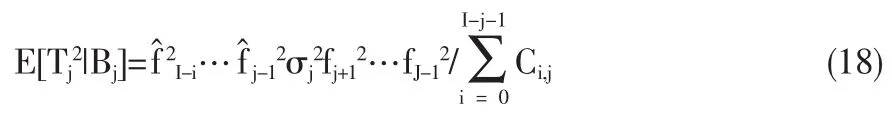
把未知参数fj和分别替换为各自的无偏估计量和，得到参数估计误差的如下估计式（记为

综合（15）式和（19）式就得到了各事故年的预测均方误差的估计量为

先考虑两个事故年i和k，设i＜k。那么

对上式右边第一项，应用独立性假设，得到

Var(Ci,J+Ck,J|DI)=Var(Ci,J|DI)+Var(Ck,J|DI)

对第二项，展开为三项之和。最后整理后，得到

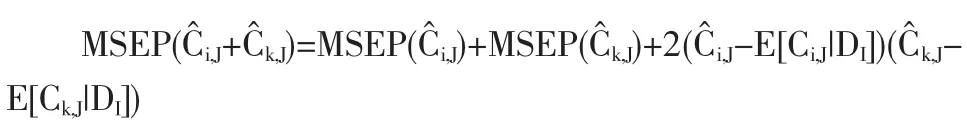
一般地，未决赔款准备金总额的预测均方误差[4]有如下Mack公式：

3 数值实例

下面以数值实例说明如何利用Mack模型计算未决赔款准备金的预测均方误差，这里采用R语言对其进行数值实现。其累计赔款数据见表2。

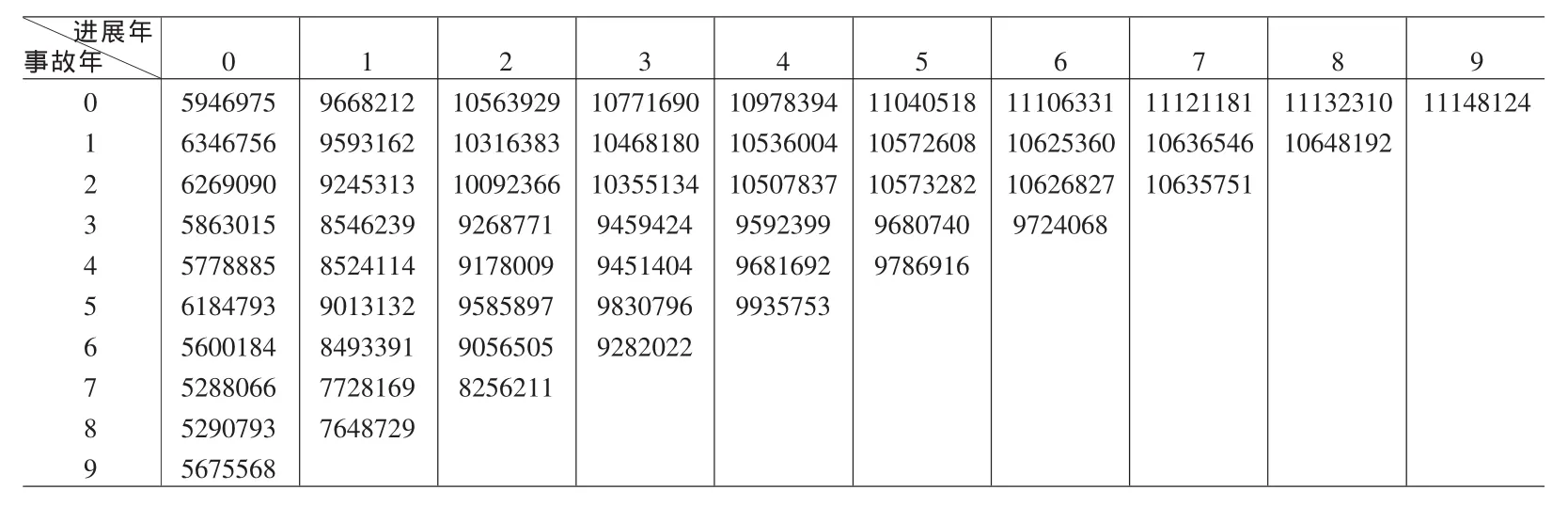
表2 累计赔款数据

应用上一节的结论，编程计算得到如表3的主要数值结论。

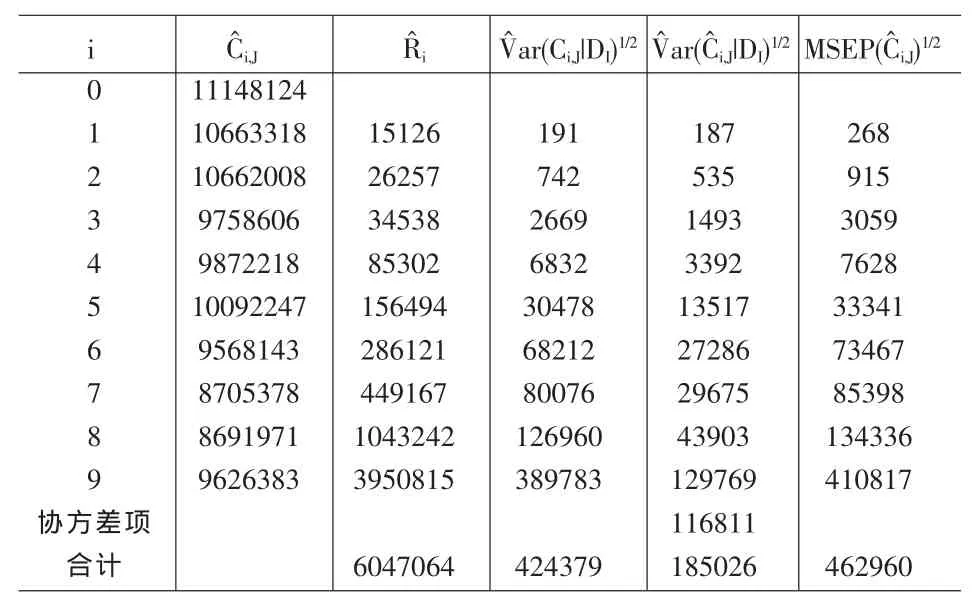
表3 链梯法准备金估计以及预测均方误差估计

另有一增量赔款数据（见表4）出现在其后很多文献中。相应的结论见表5。

表4 增量赔款数据

表5 链梯法准备金估计以及预测均方误差估计

4 结论

（1）未决赔款准备金的预测均方误差随着事故年已知信息的减少而增加。举例来讲，对第10个事故年，仅有一个赔款数据，此时信息最少，所以其准备金的预测均方误差最大，该结论是符合实际情况的，因为当已知的信息越少时，估计的误差就会越大。

（2） 估 计 结 果 的稳健性。在Mack模型的假设下，得到的总的未决赔款准备金估计的变异系数比较小，部分地说明了该方法比较稳定。

（3）Mack模型比较容易理解，在计算机上易于编程计算。

另外，本文采用R语言进行算法实现，所有的算法模块化、可操作性强、处理速度快，其实现过程也有很高的灵活性，例如事故年和进展年可根据需要自由选择、输入流量三角形数据，所有的结果自动实现等等。随着精算实务中对未决赔款准备金的波动性的逐渐重视，本文的研究对保险公司在评估准备金方法中引入随机性方法——Mack方法，将具有十分重要的理论意义和实践价值。

[1]T.Mack.Distribution-free Calculation of the Standard Error of Chain Ladder Reserve Estimates[J].ASTIN Bulletin,1993,23(2).

[2]张连增.未决赔款准备金评估的随机性模型与方法[M].北京：中国金融出版社，2008.

[3]G.Taylor，F.R.Ashe.Second Moments of Estimates of Outstanding Claims[J].Journal of Econometrics,1983,(23).

[4]M.V.Wüthrich，M.Merz.Stochastic Claims Reserving Methods in Insurance[M].Chichester:John Wiley&Sons,Ltd,2008.