湖南柿竹园野鸡尾尾矿库渗流与稳定性有限元分析

李青石，李庶林，周舒威，陈际经

（1.厦门大学 建筑与土木工程学院，福建 厦门361005；

2.湖南杮竹园有色金属有限责任公司，湖南 郴州 423037）

0 引言

尾矿库是维持矿山正常生产的重要设施之一，其坝体高度随着矿山企业不断运作而升高，但安全性能却在不断地降低。在众多因素中，渗流是影响尾矿库稳定性的重要因素。因此，对于尾矿库的渗流稳定性分析尤为重要。

目前渗流分析方法主要有解析法、实验方法以及数值方法。数值方法中的有限元法以其理论完善，能够适应各种复杂边界条件以及商业软件的成熟，已经得到很多研究者的青睐，并且近几年来在渗流稳定性计算方面获得众多进展［1－9］。

尹光志等［2－3］以试验数据为基础，采用 Slide5.0软件对尾矿坝的稳定性进行了计算，获得了尾矿坝在不同工况下的稳定性结果；同时，利用2D-FLOW计算软件，对龙都尾矿库在不同条件下的渗流进行了模拟计算；曹林卫等［4］通过考虑位移场和渗流场，对尾矿坝的耦合响应特性进行了模拟，获得坝体变形、浸润线等重要指标；敬小非等［5］建立了流固耦合模型，得到了尾矿坝渗流场影响下的位移场和应力场，以及在洪水情况下浸润线埋深；王强等［6］利用 ANSYS热模块比拟分析渗流场，计算渗流作用所产生的应力场，从渗流场与应力场的耦合数学模型出发，研究了两场相互影响作用下的尾矿坝渗流－应力耦合场；张力霆［7］等在传统的变动网格法基础上，提出了尾矿库渗流场的改进有限元分析方法；李根［8］等利用FLAC3D计算软件对尾矿库进行了渗流数值模拟计算，对尾矿库的渗流速度矢量做了分析，并研究了水头、梯度和比降对动水压力的影响；王飞跃［9］等在深入剖析尾矿坝浸润线影响因素的基础上，提出反映阶段影响因子的浸润线矩阵，并说明了基于浸润线矩阵的尾矿坝稳定分析方法。

根据文献［10］提出的渗流计算方法，并结合了强度折减法，本文以湖南柿竹园野鸡尾尾矿库为研究背景，用ANSYS10.0软件建立了该尾矿库的渗流计算模型和静力分析模型，确定该尾矿库浸润线及水头分布情况，并分析了尾矿库的应力、滑移面、塑性区等影响其静力稳定性的要素，同时研究探讨了库区水位变化对尾矿库稳定性的影响，从渗流和静力稳定性的角度为该尾矿库的灾害防治提出适当的建议。

1 工程概况

湖南柿竹园野鸡尾尾矿库位于郴州市苏仙区白露塘镇，柿竹园南东方向约8km，地处东波野鸡尾南部山区，山势较陡，沟谷较发育，地形起伏较大，地貌单元属岩溶低山沟谷地貌。尾矿库原设计服务年限为13a，设计总库容为215×104m3，总有效库容为150×104m3，属于Ⅳ等库，采用上游法尾矿堆坝，最终尾矿堆积标高512.5m，总坝高42m。

该尾矿库曾在1985年8月25日因降雨量400mm/d的特大暴雨引起山洪爆发，泥石流淤堵截洪沟进口，洪水冲进库内以至漫顶垮坝。垮坝时坝高约40m，已堆存尾砂约 110×104m3（约 150×104t），垮坝时冲跑尾砂约100×104t，后又陆续处理尾砂20×104t，库内残存尾砂约 30 ×104t。

2001年新的尾矿库在原有库址上进行重建，初期坝体为碾压堆石透水坝，以原有残留尾矿作加固处理后为地基，坝底标高475.80m，坝顶标高492m，坝高16.20m，上游边坡为 1：1.75，下游边坡为 1：2，坝上游坡设反滤层。上、下游边坡采用干砌石护坡。后期仍采用上游法尾矿堆坝，设计平均堆积坡度1：3，最终堆积标高514m，总坝高38.20m，总库容约124.9×104m3，有效库容 84.0×104m3，设计服务年限 9年。尾矿堆积坝还可继续上升至516m，可新增有效库容12.4×104m3，可为选厂继续服务1.3年。

鉴于该尾矿库在1985年的事故对库区的居民和周边环境都造成了极其恶劣的伤害，虽然新建的尾矿库目前运行较为正常，但是诸如边坡滑移，库区水位上升引起的失稳等潜在的安全隐患不容忽视。因此，针对该尾矿库所做的渗流与稳定性分析对检验其正常生产、灾害预防具有十分重要的意义。

2 渗流场有限元法分析及浸润线确定

2.1 渗流场与温度场理论的相似性［10］

2.1.1 基本理论的相似性

根据渗流基本理论可知，多孔介质满足达西定律：

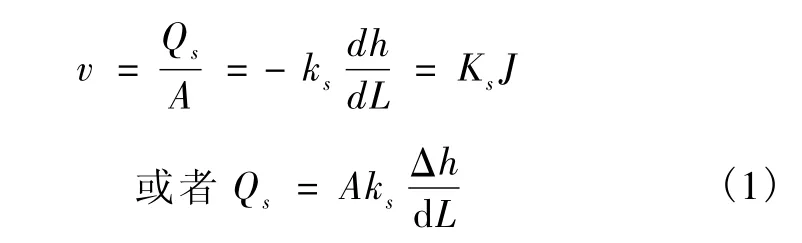
其中：Qs——渗流量；

A——断面面积；

h——测压管水头；

ks——渗透系数；

L——渗径长度；

v——断面平均流速；

J——渗透坡降。

而热传导定律（傅里叶假设）为：

其中：Qr——热（流）量；

A——断面面积；

dT/dn——温度场梯度值；

q——热传导热流强度；

kr——传热系数。

2.1.2 微分方程的相似性

（1）渗流场微分方程：

不可压缩各项异性非均质无源稳定渗流微分方程为：

其中：ksx、ksy、ksz为 x、y、z方向的渗透系数；

温度场微分方程：

对于无热源的各项异性非均质稳定热传导微分方程为：

其中：krx、kry、krz为x、y、z方向的热传导传热系数。

初始条件与边界条件的相似性

渗流场的初始条件：h|t=t0=h（x，y，x）

热传导温度场的初始条件：T|t=t0=T（x，y，x）

第一类边界条件：

渗流场：h（M，t）|Mes1= φs（M，t）

温度场：T（M，t）|Mes1= φr（M，t）

其中：h（M，t）、T（M，t）分别为时刻 t点M的测压管水头值和温度值；φs（M，t）、φr（M，t）分别为边界上给定的已知测压管水头和温度函数；M为边界S1上的点。

第二类边界条件：

其中：ksn、krn分别为沿边界法线方向的渗透系数和导热系数；∂h/∂n、∂T/∂n分别为渗流场和温度场沿边界法线方向的梯度值；vs2（M，t）、qs2（M，t）分别为边界上给定的已知流速和热流强度函数；M为边界S2上的点。

在不透水边界和绝热边界上，则有vs2（M，t）=0和qs2（M，t）=0。

通过对非饱和土渗流场与温度场的比较分析，非饱和土中水的渗流与温度场的热传导都遵循质量（或能量）守恒定律、微分方程都满足连续性条件，且

温度场：初始条件与边界条件也具有相似性，为后续应用ANSYS软件的热分析功能进行尾矿库中非饱和土的渗流计算奠定了基础。

2.2 渗流计算在ANSYS中的实现

由于尾矿库坝体中的渗流有自由水面存在，浸润线以下为饱和土，其渗透系数一般为常数，浸润线边界条件的法向渗流速度为零，而浸润线以上为非饱和土，其渗透系数是含水量的函数，一般可假设为0，即浸润线以上部分不参与计算。然而，浸润线的位置在计算前是未知的，所以在ANSYS中，仅仅假设上下游的水头，无法解决渗流问题，必须首先计算浸润线。因此，采用迭代算法，先任意假定浸润线的位置和渗出点，然后按假定的边界条件进行渗流计算，根据计算结果调整浸润线的位置，反复试算调整，直到两次计算浸润线差值小于给定误差限为止。若按照常规有限元计算方法，往往需要反复网格划分。本工程采用ANSYS提供的“死活”单元技术，直接将处于浸润线上部的单元杀死，只激活处于浸润线下部的单元。然后施加相应的边界条件进行分析；并根据计算结果调整单元的死活，相应修正边界条件后重新计算直到达到计算精度［11］。

需要注意的是，由于这种“死活”单元技术的基本对象是单元，因此，如果要得到足够的精度和足够光滑的浸润线，必须要将网格划分得足够密。由计算步骤来看，分析将需要反复进行大量重复操作，包括验证单元是否高于浸润线、激活或杀死单元、施加相应边界条件等，如果全部采用人机交互进行，工作量很大。只有采用ANSYS提供的APDL语言对模型进行参数化编程，才能将问题简化。

2.3 渗流计算模型

图1 尾矿库渗流有限元计算模型Fig.1 Finite elem entm odel for seepage of the tailing pond

渗流计算模型所选取的剖面为尾矿库具有代表性的最大纵剖面，如图1所示。模型上划分了6435个单元，6629个节点，单元采用 ANSYS中的PLANE55四边形单元，适用于分析渗流。

2.4 尾矿库土层力学参数

图2 尾矿库各地层分布情况Fig.2 The stratum in the tailing pond

根据地质资料，通过概化处理，把整个尾矿坝划分为4种材料区，即初期坝的堆石体、尾粉砂1、尾粉砂2和基底，如图2。材料的物理力学性质分别通过土工试验获得（表1）。初期坝为碾压堆石透水坝，没有测试该材料的物理力学性质，按经验选取。

表1 尾矿库土层力学参数Tab le 1 M echanical param eters of the soil in the tailing pond

2.5 结果分析

通过ANSYS有限元软件对尾矿库进行二维渗流场有限元计算分析。计算过程中，利用热流有限元与二维计算的相似性，以热流分析模型进行计算，并且根据 ANSYS中“生死单元”命令不断迭代浸润面。假定上游位置水头高度距离地面高度为 H=3m，水头高度46.06m。最终计算结果渗流量仅为0.178435×10－6m3/s，尾矿库的总水头与渗流方向如图3，图4所示。

如图5所示，压力水头为0的等值线即为尾矿库的浸润线，近似为二次抛物线，与工程勘察情况基本相符。浸润线的出溢点位置在初期坝坝顶以下，与初期坝坝顶的垂直距离为4.2m。

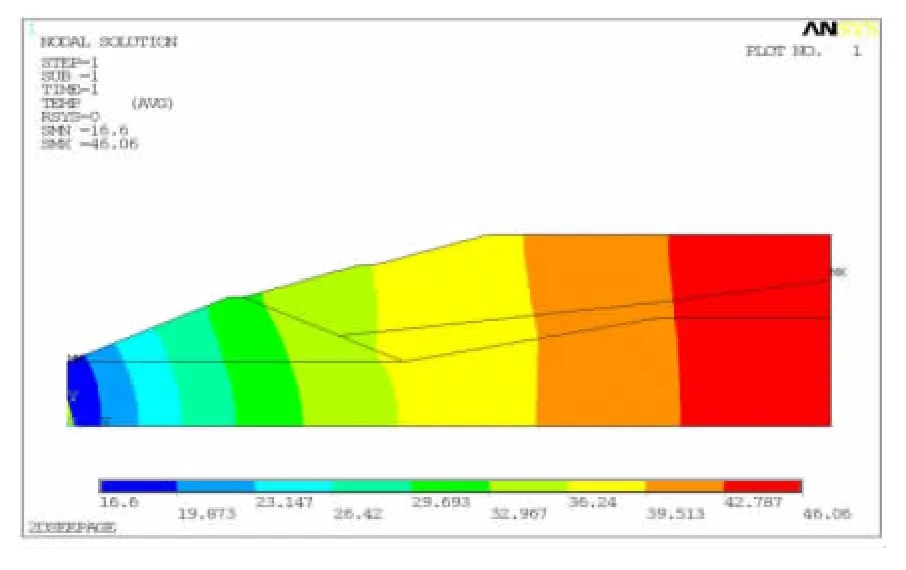
图3 尾矿库总水头云图Fig.3 Total waterhead contour of the tailing pond

图4 尾矿库渗流方向示意图Fig.4 Seepage direction of the tailing pond

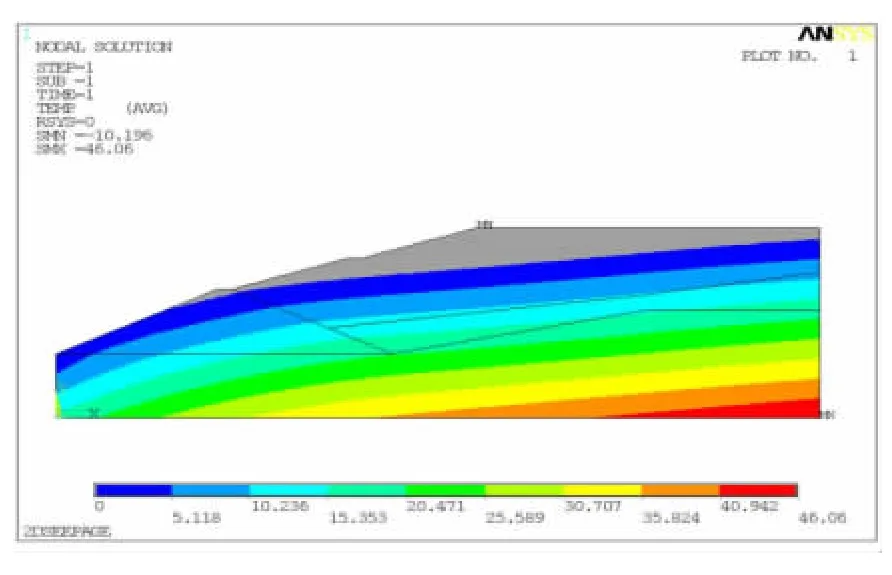
图5 尾矿库压力水头云图Fig.5 Pressure W aterhead Contour of the Tailing Pond

3 尾矿库稳定性分析

本次尾矿库的静力稳定性有限元分析，共划分了6435个单元，6629个节点，底部边界施加x、y方向上的位移约束，左右边界施加x方向上的位移约束。整个模型受重力荷载作用，并且进行“水土合算”，浸润线以上土体采用自然容重，而浸润线以下则采用饱和容重。在计算过程中，采用理想弹塑性本构关系以及岩土体有限元分析中常用的Drucker-Prager屈服准则。

3.1 塑性区

如图6所示，尾矿库的塑性区主要集中在尾矿库上游部位以及深部地层中，对尾矿库的稳定性不会造成很大影响，但是初期坝的外坝脚处存在应力集中，出现了屈服，该处最大等效塑性应变达到0.224。

3.2 应力场分析

从图7、图8可以看出，尾矿库的第一主应力出现在后期堆坝中部和尾矿库的上游区段，大小为118.367Pa，远小于该处尾砂的强度值；尾矿库的最大压应力出现在尾矿库以下的深部土层中，大小为1.29MPa。因此，尾矿库各层土体都处于应力稳定状态，并未超出其强度指标。

图6 强度折减前等效塑性应变图Fig.6 Equivalent p lastic strain before strength reduction

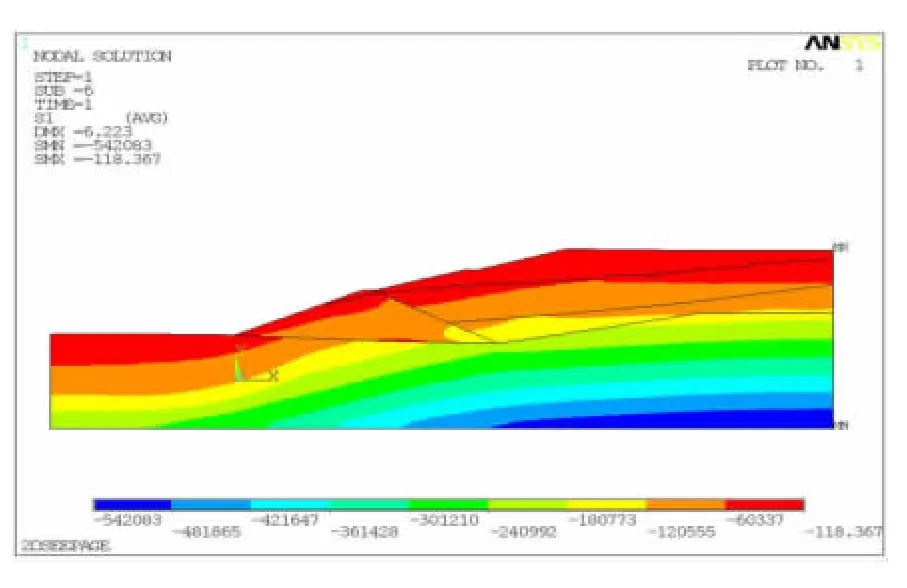
图7 第一主应力Fig.7 The 1st principal stress

3.3 可能滑动面的计算

在弹塑性有限元静力计算中，通过不断降低坡体和滑动面的强度参数（粘聚力 C和内摩擦角 φ），使系统达到不稳定状态，即有限元静力计算不收敛，由此而获得的强度折减系数就是滑坡稳定系数［13］。在计算过程中将坡体和滑动面的强度参数（粘聚力C和内摩擦角φ）逐步折减，即：

图8 第三主应力Fig.8 The 3rd p rincipal stress

式中：Fs——强度折减系数；

C0——原粘聚力；

φ0——原内摩擦角。

将折减后所得参数输入进行有限元计算，若程序计算收敛，则滑坡仍处于稳定状态；继续折减，直到不收敛为止，此时土体出现大幅度塑性滑移，滑坡最终的折减系数即为稳定系数。本文计算的尾矿库的边坡稳定系数为5.902。

图9 基于强度折减的尾矿库可能滑移面Fig.9 Potential Slip Surface of the Tailing Pond Based on Strength Reduction

尾矿库的可能滑移面如图9所示，从距离坝顶25m处，沿圆弧面，经过初期坝内坝脚处，延伸至坝前土层中部，一部分继续延伸至距离初期坝外坝脚30m处，另一部分与初期坝外坝脚相交。由图中可以看出，尾矿库的边坡一旦破坏，将有可能沿图示的圆弧面向下滑移，同时，坝前30m范围内的土层将可能随着边坡的滑移出现上拱。

4 库水位变化对尾矿库稳定性的影响

尾矿库坝体渗流是由库区水位和下游水位的水头差引起的，位于浸润线以下的坝体部分都处于渗流场中受到渗流的影响［7］。库区水位的变化带动了水头差的变化，必然使得浸润线以下土体的强度、渗透力等因素受到影响，导致整个尾矿库的稳定性发生变化。如图10所示，本文沿坝坡方向，选取初期坝坝脚、三个坡段的中点和坡顶为关键点，共7个关键点，并分析其在库水位变化时的位移以及应力变化。

图10 关键点选取Fig.10 Key poin ts

4.1 关键点的位移变化

分析关键点x方向位移与水位到地表高度H的关系，从表2中可以看出，库区水位升高时，坝坡各点位移没有明显变化，产生滑坡的可能性较小，对于尾矿库整体稳定不会产生很大影响。

4.2 关键点的应力变化

分析关键点第三主应力与水位到地表高度H的关系，从表3中可以看出，库区水位升高时，坝坡各点第三主应力呈逐渐增大的趋势，对于本工程而言，增大的幅度并不明显，因此，该尾矿库从自身材料性质上具备一定的抵抗水位升高造成破坏的能力。

4.3 对稳定性的影响

从以上表2、3中x方向位移、第三主应力变化幅度不大的情况来看，地下水位的小幅变化（H=1～11m）对于尾矿库稳定性的影响不大，尾矿库的安全系数变化不大，并且都大于规范要求的安全系数，即表明尽管当库区水位升高时，坝体的浸润线抬高，土体的含水量增大，抗剪强度降低，由于水头差的存在使得坝体出现较大的渗透力，致使尾矿库稳定性下降，但是尾矿库仍有很大的安全储备。

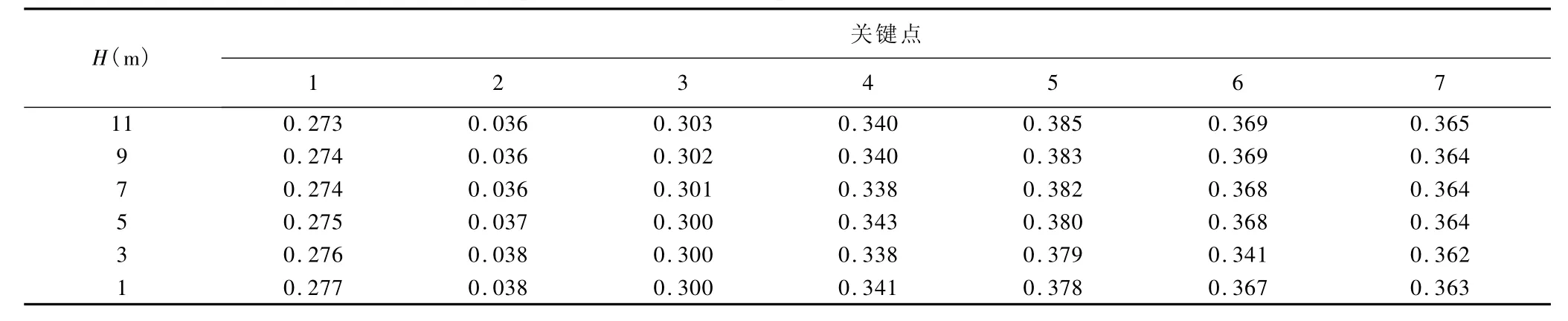
表2 不同水位对应的关键点x方向位移（m）Table 2 Xdirection disp lacem ent of the key poin ts under different w ater level cond ition（m）

表3 不同水位对应的关键点第三主应力（Pa）Tab le 3 The 3rd pincipal stresses of the key points under different water level condition（Pa）

5 结语

对于尾矿库坝体的稳定性进行渗流分析和静力分析计算是尾矿库坝体稳定分析的重要工作，有限元计算［14］可以直观地反应出尾矿库的运行状况，野鸡尾尾矿库在渗流条件下的稳定性良好，安全系数较高。

尾矿库的浸润线是尾矿库的生命线，库水位的升高带动了浸润线的升高和浸润线以下土体的强度降低，为尾矿库的稳定性带来重大隐患。因此，建议在野鸡尾尾矿库的治理中应做好以下几点：

（1）控制尾矿库内水位，增设坝体排水设施，降低浸润线，并密切注意库区水位、干滩长度及最低安全超高的控制［15］。

（2）加强尾矿库的安全监测，在尾矿库内外设置孔隙水压力仪及坝体变形、位移等观测设备，进行实时监测，建立尾矿库管理档案，及时发现和处理隐患。

（3）加大堆坝粗砂产量，提高坝坡的排水渗透性，保证坝坡脚排水垫层的透水能力。

（4）做好尾矿堆积坝外坡坡面雨水冲刷的防护工作，避免局部滑坡引起坝坡的滑移变形。特别在汛期应做好必要的抢险准备工作，确保安全渡汛。

［1］胡少华，王 涛，杨 凡，等.某尾矿库的渗流与稳定数值计算分析［J］.科技情报开发与经济，2010，20（12）：140 －142.HU Shaohua，WANG Tao，YANG Fan，et al.Calculating and analyzing the seepage and stability of a tailing pond［J］.Sci-Tech Information Development ＆ Economy，2010，20（12）：140 －142.

［2］尹光志，魏作安，万 玲.龙都尾矿库地下渗流场的数值模拟分析［J］.岩土力学，2003，24（S）：25 －28.YIN Guangzhi，WEI Zuoan，WAN Ling. Numerical simulation analysis about seepage field of Longdu tail bay［J］.Rock and Soil Mechanics，2003，24（Supp）：25 －28.

［3］尹光志，李愿，魏作安，等.洪水工况下尾矿库浸润线变化规律及稳定性分析［J］.重庆大学学报，2010，33（3）：72 －75.YIN Guangzhi，LI Yuan，WEI Zuoan，et al.Regularity of the saturation lines’change and stability analysis of tailings dam in the condition of flood［J］.Journal of Chongqing University，2010，33（3）：72 －75.

［4］曹林卫，彭向和，李 德，等.变形场和渗流场耦合作用下的尾矿坝静力稳定性分析［J］.重庆建筑大学学报，2007，29（5）：112 －118.CAO Linwei，PENG Xianghe，LIDe，et al.Analysis of the static stability of tailings dam under coup led deformation and seepage fields［J］.Journal of Chongqing Jianzhu University，2007，29（5）：112－118.

［5］敬小非，邓 涛，谭钦文.基于ABAQUS有限元软件对尾矿坝的稳定性预测［J］.现代矿业，2009，（2）：74－77.JING Xiaofei，DENG Tao，TAN Qinwen. Stability forecasting of tailings dam by ABAQUS finite element software［J］.Morden M ining，2009，（2）：74－77.

［6］王 强，鲁炳强，王水平，等.尾矿坝渗流 －应力耦合场的有限元分析［J］.现代矿业，2009（3）：74－77.WANG Qiang，LU Bingqiang，WANG Shuiping，et al.Finite element analysis on seepage and stress coupled field of tailing dam［J］.Morden M ining，2009.（3）：74 －77.

［7］张力霆，周国斌，谷 芳，等.库区水位急剧变化对尾矿库坝体稳定的影响［J］.金属矿山，2008，（8）：119 －122.ZHANG Liting，ZHOU Guobin，GU Fang，et al.Influence of the rapidly changing reservoir level on the stability of tailing dam［J］.Metal M ine，2008，（8）：119 －122.

［8］李 根，王来贵，陈 雷，等.某尾矿库渗流稳定性的数值模拟［J］.金属矿山，2008，（9）：123－125.LI Gen，WANG Laigui，CHEN Lei，et al. Numerical simulation of the seepage stability of a tailing reservoir［J］.Morden Mining，2008（9）：123－125.

［9］王飞跃，杨铠腾，徐志胜，等.基于浸润线矩阵的尾矿坝稳定性分析［J］.岩土力学，2009，30（3）：840 －844.WANG Feiyue，Yang Kaiteng，Xu Zhisheng，et al.Stability analysis of tailings dam based on saturation line matrix［J］.Rock and Soil Mechanics，2009，30（3）：840－844.

［10］杨根春.中小型土石坝渗流数值模拟及边坡稳定分析［D］.成都：西华大学硕士学位论文，2010.YANG Genchun.Numerical simulation of seepage on small earth-rock dam and slope stability analysis［D］.Chengdu：Xihua University，2010.

［11］贺晓明.基于 ANSYS的大坝渗流分析研究［D］.西安：西安理工大学硕士学位论文，2006.HE Xiaoming.Research on analyzing dam seepage based on ANSYS［D］.Xi’an：Xi’an University of Technology，2006.

［12］张 施，汪 斌.基于FEM强度折减系数法的某库岸斜坡稳定性分析［J］.湖北水利水电职业技术学院学报，2009，2（1）：17－21.ZHANG Shi，WANG Bin.Stability analysis of a reservoir slope based on themethod of FEM strength reduction［J］.Journal of Hubei Water Resources Technical college，2009，2（1）：17－21.

［13］刘明维，郑颖人.基于有限元强度折减法确定滑坡多滑动面方法［J］.岩石力学与工程学报，2006，25（8）：1544－1549.LIU M ingwei，ZHENG Yingren，determ ination methods of multi-slip surfaces landslide based on strength reduction fem［J］. Chinese Journal of Rock Mechanics and Engineering，2006，25（8）：1544 －1549.

［14］陈津端，李仕武，宁立波，等.某尾矿坝体浸润线有限元模拟分析［J］.湖南科技大学学报（自然科学版），2007，22（4）：23－25.CHEN Jinduan，LI Shiwu，NING Libo，et al.Analysis of finite element method by simulation on one tailing dam saturation line［J］. Journal of Hunan University of Science＆Technology（Natural Science Edition），2007，22（4）：23 －25.

［15］齐清兰，张力霆，谷 芳，等.影响尾矿库渗流场的因素及降低浸润线的措施［J］.金属矿山，2009，（12）：35－37.QI Qinglan，ZHANG Liting，GU Fan，et al.the factors influencing the seepage field of tailing dam and the measures lowering the seepage line［J］.Metal Mine，2009，（12）：35－37.