一种改进的区域滑坡危险性评价模型及其应用

王 杰，马凤山，郭 捷，魏爱华，巩城城

（中国科学院 地质与地球物理研究所工程地质力学重点实验室，北京 100029）

0 引言

根据中国地质环境监测院提供的资料，在滑坡、崩塌、泥石流、地裂缝、地面沉降这些主要的地质灾害中，滑坡占灾害总数的75％。近期伴随着极端气候条件的出现、地壳活跃程度的增高，滑坡的数量更是急剧增加。滑坡的发生往往会给人类的生命、财产带来巨大的损失。从20世纪70年代开始，国内外已有很多学者致力于滑坡危险性评价的研究，而且提出了多种评价模型。例如，Martin Cross采用矩阵评价方法，按滑坡敏感性指标的大小对英国Derbyshire地区进行了滑坡危险性区划［1］。Saro Lee等利用Bayesian概率模型，研究了韩国 Janghung地区的滑坡危险性［2］。Ranjan Kumar Dahal等应用证据权重模型对日本四国岛的一个集水区作了滑坡危险性评价［3］。Adnan Ozdem ir等利用条件概率模型对土耳其的Gelendost地区进行了滑坡危险性评价［4］。Falaschi F等应用逻辑回归与神经网络相结合的模型对意大利Serchio河谷地区做了滑坡危险性评价［5］。殷坤龙、晏同珍引入信息量及二态变量回归分析法建立了关于斜坡稳定性的两种预测模型，并编制了汉江河谷旬阳段斜坡稳定性分区图［6］。黄润秋等建立了逻辑信息模型，并对模型进行了模糊逻辑扩充，对整个三峡库区近千公里岸段斜坡稳定性进行了空间预测［7］。张春山、张业成运用灰色关联度分析模型对黄河上游地区的崩滑流灾害进行了危险性评价［8］。戴福初等采用两类和单类支持向量机对香港地区进行了滑坡灾害空间预测［9］。总的来说，不同的评价模型各有其特点，应根据评价区的实际情况和可获得的基础数据来选取合适的模型。由于滑坡机理的复杂性，各个评价模型的精度都是有限的，很多模型仍有待于改进和完善。因此，本文将尝试把一种新的滑坡危险性计算方法与层次分析法、条件概率模型相融合，建立一个改进的区域滑坡危险性评价模型，并利用GIS二次开发编程实现该模型，最后将其应用于对陕西省麟游县滑坡危险性评价工作中。

1 评价模型

模型建立在工程地质类比法的基础上，即假设将来的滑坡是在与过去相同的导致坡体失稳的工程地质条件下发生的。借鉴条件概率模型［4］中的做法，用区域内滑坡的面密度表示该区域滑坡发生的危险性。然后，用已滑地区的工程地质条件及与其对应的滑坡危险性去推断未滑地区滑坡发生的危险性大小。

评价过程中首先通过野外调查确定区域内与滑坡发生密切相关的因素作为致险因子，然后通过层次分析法确定各个致险因子的权重，接下来通过统计和曲线拟合确定某个因子单独作用下滑坡的危险性，最后再把评价单元内所有致险因子造成的危险性加权求和，得到最终的滑坡危险性。具体细节详述如下：

1.采用等大矩形网格对评价区域进行剖分，网格大小根据评价范围和剖分后单元内统计值的变化情况来确定，要求不同评价单元间致险因子的值、滑坡危险性值都有较大的变化区间。

2.致险因子权重的确定采用层次分析法［10］，这是一种定性与定量相结合的方法，有着严格的数学基础。实施过程文献10中有着详细的介绍，不再赘述。

3.对于不考虑致险因子间相互影响时单个因子造成的滑坡危险性，具体研究方法如下：

1）对于能够定量描述的因子，比如图1所示的水系，可以首先通过GIS叠加分析得到每个评价单元内水系的线密度，进而统计线密度属于某一区间的单元数和这些单元内的滑坡灾害点数，从而得到不同线密度取值区间对应的滑坡面密度值，然后取区间的右端点值和该区间对应的滑坡密度值组成数据对（x，y）作为基础数据点。由于某个因子不存在时其影响为0，所以再添加（0，0）点。用这些点拟合滑坡发生的危险性与致险因子之间的函数关系，然后把每个评价单元中致险因子值代入拟合结果，计算出单元内的该因子造成的滑坡危险性。上述这种选取基础数据点的方法在本文中首次使用，并无先例。

图1 水系剖分示意图Fig.1 M esh generation for river system

拟合时的原始曲线采用六次多项式：

其中：Li（x）——未考虑致险因子间相互作用的条件下致险因子取值为x时的滑坡危险性。

通过统计得到多组（x，Li（x）），代入式（1）得到下面的含有七个未知数的方程组（这个方程组可以是超定的）。

由线性代数知道，任意m×n阶矩阵A，只要其列向量线性无关，那么它一定能分解成A=QR，其中Q是m×m的正交矩阵，R是m×n的上三角矩阵［11］。上面的方程组中，各列元素的比值都不成比例，满足所有列向量线性无关的要求。因此，可以分解得到矩阵Q和R。所以，式（2）变换为：

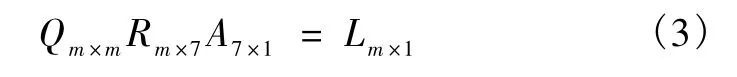
其中，Q、R乘积对应由xi的不同次幂组成的系数矩阵，A是未知数ai组成的矩阵；L代表后边Li（x）组成的常数项。因为Q是正交矩阵，即QT×Q=E，上式左乘QT得：

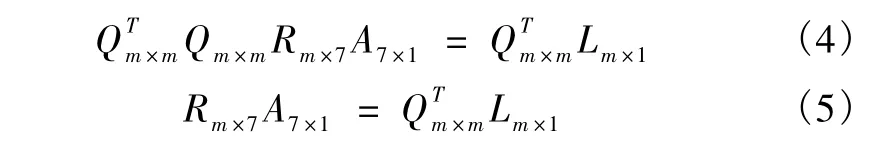
式（5）右端是一个由常数组成的 m×1的列向量，R是一个上三角矩阵，展开后为：

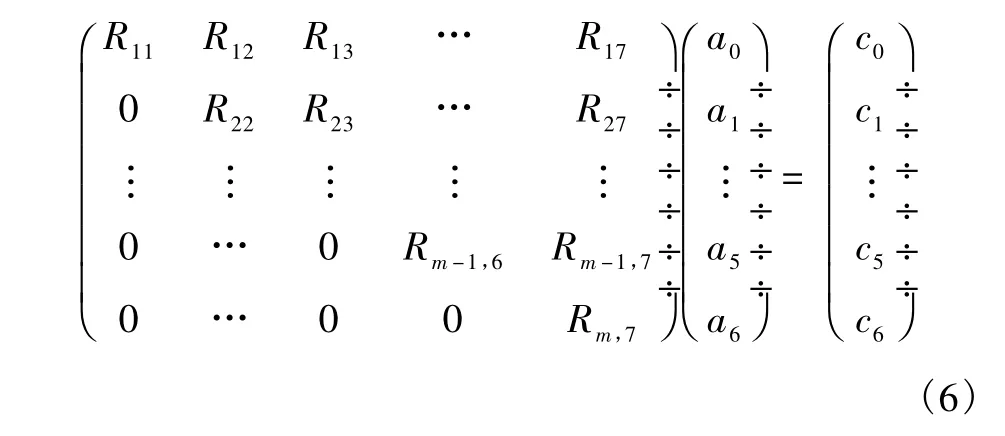
可见，通过最后一行可以得到未知数a6，然后代入倒数第二行可求得a5，依次回代就得到了所有未知数ai的值，继而求得函数Li（x）的表达式。然后，在每个评价单元中用该式去求单个因子造成的滑坡危险性。

2）对于图2所示的“工程地质岩组”这种仅适于定性分类，较难定量表达的因子可以把不同类别中滑坡的面密度作为该类别的危险性指标。某一单元内该因子的滑坡危险性可以用下式计算：

其中，Li（xj）代表 i因子中包含的第j类因素的危险性；Aj代表单元内第j类因素所占的面积；A代表单元的总面积；n代表i因子内部可分成的类别总数；Li代表评价单元中i因子造成的滑坡危险性。

图2 岩性剖分示意图Fig.2 M esh generation for lithology

4.把某一单元内通过单因子分析得到的滑坡危险性Li进行归一化。然后，乘以该因子的权重Wi，得到该因子存在造成的滑坡危险性。再把所有因子造成的危险性相加，从而得到考虑多个致险因子共同作用下滑坡发生的总危险性L：

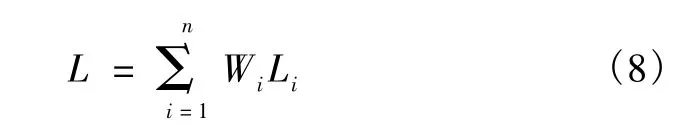
2 评价模型的编程实现

2.1 模型功能的实现过程

在传统滑坡危险性评价工作中多采用栅格数据作为底图进行叠加。这种方法在小区域危险性评价中得到了较好的应用。如果研究的范围较大，把各种矢量数据全部转化为栅格数据是非常耗时费力的。另外，表达同样多的信息，栅格数据占用的存储空间相对较大，而且同时打开大量栅格数据时，对电脑配置要求也较高。为了尽量避免这些弊端，在本文模型实现过程中，通过空间查询、属性查询以及拓扑操作等接口实现了矢量数据间以及矢量与栅格间的直接叠加，放弃了所有的操作都依赖栅格数据的传统做法。

模型实现方法如图3所示，首先通过空间查询得到一个外切评价区域（红线表示评价区）的矩形范围，然后以等大的小矩形网格在该范围内划分评价单元。这些矩形网格作为一个要素类存储到一个shape files型的矢量文件中，每个网格都包含以各致险因子名称命名的属性字段，用于保存该网格与某个致险因子叠加求交后得到的网格内致险因子的量值。如图3中阴影部分的网格，其与致险因子层的水系进行叠加求交，得到该网格内水系的总长度，再除以网格面积即可得到水系面密度，这个面密度值就存放在该网格的“水系”字段中。另外，每个网格还有以致险因子的名称后加数字2命名的属性字段，用于存储各因子单独存在时造成的滑坡危险性大小，最后用一个result字段存储考虑各致险因子的权重后求出的最终滑坡危险性。

图3 模型剖分、叠加原理示意图Fig.3 Theorem of m esh generation and overlay in the m odel

处理诸如DEM这样的栅格数据时，因为GIS系统中矢量数据与栅格数据是不能直接叠加的，所以采取了一个等效的办法，即首先得到一个矩形网格区域，然后裁剪该区域包含的栅格图像，最后对裁剪下来的栅格数据进行求平均坡度等操作。

接下来将是结果展示。首先裁掉研究区域以外多余的部分，然后根据结果字段result中的值对所有单元格进行着色渲染，不同的颜色表示不同的危险性等级，最后的结果还可以转换成栅格文件来保存。

2.2 软件界面

图4为模型实现的软件界面，在“模型”选项卡下分布有11个按钮，用于完成危险性评价工作。其中“网格划分”按钮用于得到图3中所示的网格单元；“水系”、“道路”、“断层”3个按钮分别用于得到各网格单元内水系、道路、断层的线密度。“平均坡度”按钮用于得到各个网格单元内的平均坡度值。

“单因子统计”按钮用于求不考虑因子间的相互影响时单个致险因子造成的滑坡危险性。在“间隔”选项卡下，如图5所示，可按某一间隔依次截取一定的统计区间，然后统计出属于各个区间内的单元个数、滑坡数和滑坡的面密度值。“分段赋值”会根据分段统计结果去拟合滑坡危险性与各个致险因子之间的关系曲线，然后通过该曲线求得各个统计单元格内某因子单独作用下滑坡的危险性大小，完成评价模型中第3步中所述的内容。

图4 模型实现模块界面Fig.4 Software interface for realizing them odel

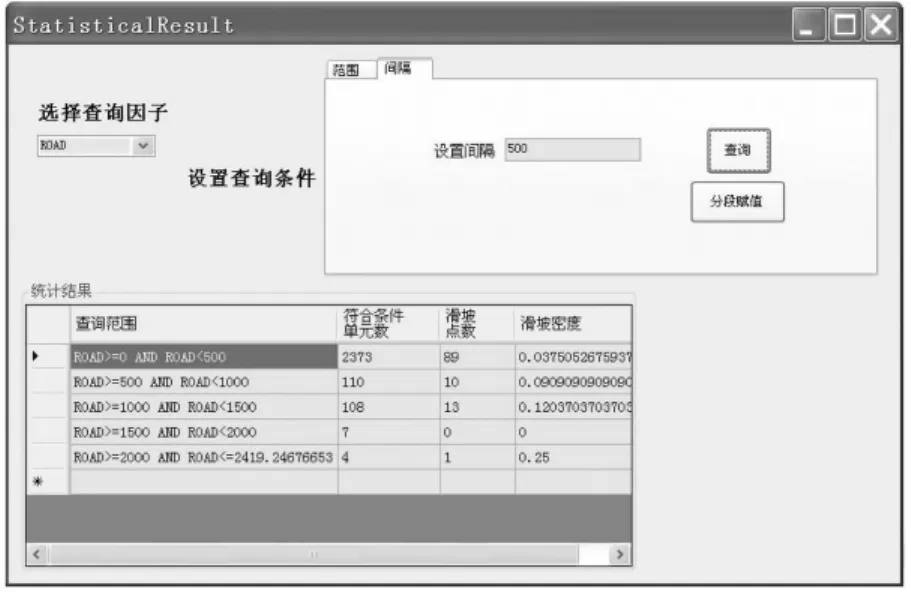
图5 指定间隔的单因素统计Fig.5 Single factor statistics through a fixed interval

图6显示的是图4中“因子权重”按钮下的界面，它通过层次分析法求得各个因子相互作用下单因子权重的大小。按照层次分析法中建立相互关系判断矩阵的原则在“因子关系矩阵”表格中输入表示各因子间相对重要性的数值作为矩阵的元素，然后点击“计算权重”按钮就会自动计算该矩阵的主特征向量，该向量的各个元素即为各个因子的权重。如果觉得致险因子个数太多，关系混乱，可以删除多余致险因子再进行关系矩阵的输入，系统会自动把删除的因子的权重赋值为零，如果觉得删除的不得当，还可点击“复原因子”按钮回到初始状态。

完成计算前的所有准备工作后，可以点击“求解”按钮计算各单元格的最终危险性。图4中最后的“裁边”、“等级图渲染”、“栅格输出”三个按钮是用于完成最后的出图工作。

为了验证模型的可靠性，以陕西省宝鸡市麟游县为例进行滑坡危险性区划。

3 评价模型在麟游县的应用

3.1 麟游县地质背景概述

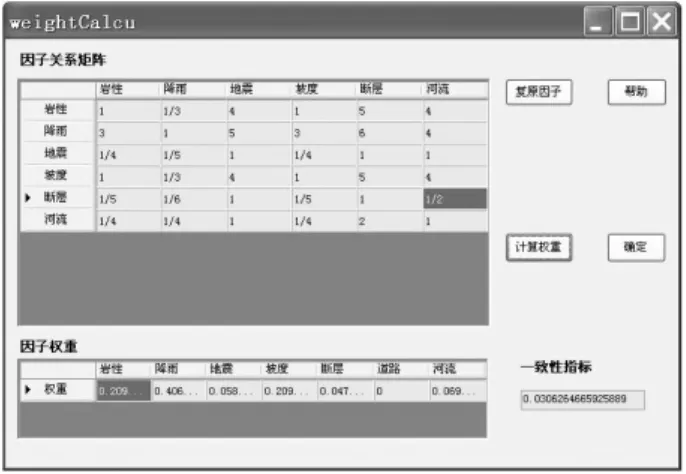
图6 层次分析法求因子权重软件界面Fig.6 Software inter face for w eights calcu lating by analytic hierarchy p rocessm ethod

麟游县位于陕西省宝鸡市东北部，总面积1740km2。总体地势西北高东南低，平均海拔1271 m，中部页岭呈东西方向隆起，构成泾河与渭河流域的分水岭，渭河支流呈树枝状，向东南方向汇聚，泾河支流向东北方向汇聚。麟游县属温带半湿润～湿润季风气候区，多年平均降雨量641.6 mm，降雨量分布情况大体是西多东少，降雨集中在7～9月，占全年降雨量的50％以上，受降雨影响，这三个月是地质灾害的高发期。

麟游县境内主要分为低中山、黄土丘陵、黄土残塬、河谷川道四种地貌类型。区域地质构造简单，并且没有区域大断裂。总体分为2个构造层，新生代地层不整合在老地层之上。地块隆升，形成黄土高原，同时也加剧了流水的侵蚀切割，致使黄土高原支离破碎，沟壑纵横、坡缓川狭、少有台塬。新构造运动相对不强烈，邻区曾有强震发生，在分区上其地震烈度为Ⅶ度。区内岩土体类型、性质及分布情况如图7所示，主要岩石是奥陶系、二叠系、三叠系、侏罗系、白垩系砂质泥岩；新近沉积、半成岩的红土层，在分水岭和丈八乡一带出露，与下伏岩体呈不整合接触关系，底部为半胶结砾岩，干燥时致密坚硬，透水性差，构成局部隔水层；风积黄土在全区大范围出露；粗砂岩主要分布在麟游县南部。

3.2 麟游县滑坡危险性分区

对于麟游县的滑坡危险性分区主要选取的致险因子有岩性、降雨、坡度、河流、道路，由于该县没有区域性大断裂通过，受断层影响较小，所以没有考虑断层因子的影响。另外，一个县域范围内不同乡镇的地震烈度变化很小，所以也没考虑场地地震烈度的影响。权重判断矩阵、因子权重和一致性指标如图8。

本文应用上述软件系统，对麟游县进行滑坡危险性区划的结果如图9所示。

图7 麟游县地质图Fig.7 Geologicalm ap of L inyou County

图8 致险因子权重计算结果Fig.8 W eights of hazard-inducing factors

图9 麟游滑坡危险性评价结果图Fig.9 Resu lt of landslide hazard assessm ent in Linyou County

下面结合野外考察资料对评价结果进行分析。在麟游县中部的页岭隆起区滑坡危险性较高，因为该区黄土大面积出露，而黄土具有高孔隙性和湿陷性，垂直节理发育，容易产生滑坡；另外，该区有一条主干路通过，由于修路的影响形成了一些人工临空面；野外考察发现的老滑坡也是该区居多，所以认为这一滑坡高危险区的出现是合理的。南部以粗砂岩、砂质泥岩为主，这两种岩性相对于黄土来说不容易造成滑坡，虽然该区河流相对密集，但是这两种岩性对河流侵蚀的抵抗能力相对较强，所以受岩性影响该区属低危险区，而在黄土大面积出露的其他地区，只要河流、道路等密集滑坡危险性就偏大。粘土是隔水层，受水流影响较小，所以在粘土出露处，即使河流发育，滑坡的危险性也只达到中等。总的来说，该滑坡危险性评价结果是可信的。

4 结论

（1）以工程地质类比法为基础，借助线性代数中的QR分解理论，提出了一种用高次多项式拟合致险因子与滑坡危险间性关系的算法，并把该算法与层次分析法模型、条件概率模型相融合，给出了一种改进的区域滑坡危险性评价模型。

（2）给出了一种新的、应用于滑坡危险性计算的基础数据提取方法，首先统计不同致险因子取值区间的滑坡面密度，然后取区间右端点值和该区间的滑坡面密度值作为拟合致险因子与滑坡危险性间关系的基础数据。这种做法能够较好的反应复杂地质条件下致险因子与滑坡危险性间的非线性、非单调的、波动变化的关系，比对致险因子进行简单的平均分段的做法更切合实际。

（3）在C#环境下，借助 ArcEngine组件自主开发了一套基于本文评价模型的软件系统，并运用该软件对陕西省麟游县进行了滑坡危险性评价，经检验，评价结果可靠，该模型具有较高的可信度，可用于今后的评价工作中。

（4）该模型也存在一个缺点，就是它需大量数据作为支撑，对基础数据的要求较高。

［1］James D.，Griffiths S.Mapping in engineering geology［M］//Cross M.Landslide susceptibility mapping using the Matrix Assessment Approach： a Derbyshire case study.London；The Geological Society 2002：267.

［2］Lee S，Choi J，M in K.Landslide susceptibility analysis and verification using the Bayesian probability model［J］.Environmental Geology，2002，43（1）：120－131.

［3］Dahal R，Hasegawa S，Nonomura A，et al.GIS-based weights-of-evidence modelling of rainfall-induced landslides in small catchments for landslide susceptibility mapping［J］.Environmental Geology，2008，54（2）：311－324.

［4］Ozdemir A.Landslide susceptibilitymapping of vicinity of Yaka Landslide（Gelendost，Turkey）using conditional probability approach in GIS ［J］.Environmental Geology，2009，57（7）：1675－1686.

［5］Falaschi F，Giacomelli F，Federici P，et al.Logistic regression versus artificial neural networks： landslide susceptibility evaluation in a sample area of the Serchio River valley，Italy［J］.Natural Hazards，2009.

［6］殷坤龙，晏同珍.汉江河谷旬阳段区域滑坡规律及斜坡不稳定性预测［J］.地球科学，1987，6（631－638.YIN Kunlong，YAN Tongzhen.Distribution regularity of landslides and prediction of slope instability nearby Xunyang，Han River Valley ［J］.Earth Science，1987，12（6）：631 －638.

［7］黄润秋，李曰国.三峡工程水库岸坡稳定性预测的逻辑信息模型［J］.水文地质工程地质，1992，19（1）：15－20.HUANG Runqiu，LI Yueguo.Logical message model of stability predication of bank slopes in Three Gorges［J］.Journal of of Hydrogeology＆ Engineering Geology，1992，19（1）：15 －20.

［8］张春山，张业成，马寅生.黄河上游地区崩塌、滑坡、泥石流地质灾害区域危险性评价［J］.地质力学学报，2003，9（02）：143－153.ZHANG Chunshan，ZHANG Yecheng，Ma Yansheng.Regional dangerous on the geological hazards of collapse，landslide and debris flows in the upper reaches of the Yellow River［J］.Journal of Geomechanics，2003，9（2）：143 －153.

［9］戴福初，姚鑫，谭国焕.滑坡灾害空间预测支持向量机模型及其应用［J］.地学前缘，2007，14（6）：153－159.DAI Fuchu，YAO Xin，Tan Guohuan. Landslide susceptibility mapping using support vector machines［J］.Earth Science Frontiers，2007，14（6）：153 －159.

［10］许树柏.实用决策方法——层次分析法原理［M］.天津：天津大学出版社，1988：6－13.XU Shubai.Practical decision making method-the Analytic Hierarchy Process［M］. Tianjin： Tianjin University Press，1988：6 －13.

［11］徐士良.常用算法程序集（C语言描述）［M］.北京：清华大学出版社，2004：63.XU Shiliang.Programs of usual algorithms（described by using C language）［M］.Beijing：Qinghua University Press，2004：63.