Robust Non-fragile PID Controller Design for the Stroke Regulation of Metering Pumps*

YU Shiming (余世明), WU Jiangjiang (吴江江) and ZHANG Duan (张端)



Robust Non-fragile PID Controller Design for the Stroke Regulation of Metering Pumps*

YU Shiming (余世明), WU Jiangjiang (吴江江) and ZHANG Duan (张端)**

College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China

This job focuses on the stroke regulation of a class of high-precision metering pumps. A parameter- tuning method of robust non-fragile PID (proportional-integral-derivative) controllers is proposed with the assumption that a PID controller has additive gain perturbations. An-infinite robust PID controller can be obtained by solving a linear matrix inequality. This approach can guarantee that the closed-loop control systems is asymptotically stable and the-infinite norm of the transfer function from the disturbance to the output of a controlled system is less than a given constant to attenuate disturbances. The simulation case shows that the control performance of the proposed strategy is significantly better than the traditional PID approach in the situation with perturbations of controller parameters.

metering pump, stroke regulation,-infinite robust control, PID control, non-fragile

1 INTRODUCTION

In recent years, the process control of petroleum processing, chemical engineering, water treatment and so on has attracted wide attention [1-5]. Metering pumps, a kind of reciprocating-type pumps, are widely used in a variety of process industries to control and/or measure composition ratio of fluid [6]. To metering pumps, most jobs focus on the improvement of their structure [7-9], and only limited literature concerns the control of them [10, 11]. The latter is a key issue in engineering practice and has not been solved effectively yet. Although flow rate can be easily regulated by changing the plunger stroke length of metering pumps, it is not practical to regulate it manually, especially in the fields with poisonous or dangerous liquids. In addition, the accuracy of manual regulation can not meet the requirement of production. Therefore, it is necessary to regulate it automatically by an electro servomechanism connected to the plunger.

An extended controller includes sensors and actuators. Some issues such as the drift of a sensor and the aging of an actuator result in parameter perturbations of a controller. This perturbation makes the performance of a closed-loop system deteriorate or even unstable. Therefore, the design of non-fragile controller that can tolerate parameter deviation is needed [12-14]. Reliable design problem for linear systems is concerned and the resulted control systems are reliable [12], in which guaranteed-cost asymptotic stability and∞performance are provided when some faults of control component (actuators or sensors) occur. The∞non-fragile observer-based control methods for continuous dynamical systems are investigated [13]. A time-delay independent sufficient condition of robust non-fragile guaranteed cost controllers is given for a class of uncertain large-scale systems with subsystems interconnected [14].

Figure 1 The structure of lead screw driving part of metering pumps

This work focuses on the PID controller design based on∞control theory in the existence of additive controller gain perturbations. The optimized solution of a linear matrix inequality (LMI) is used to construct the PID controller.

2 PID MODEL

As illustrated in Fig. 1, the plunger stroke length of the metering pump is regulated by driving a N-shaped shaft (omitted due to the limited space) connected with the lead screw that may move along the axis [15]. The smaller gear Z1 meshes with the larger gear Z2 fixed in the gear shaft. The shaft is connected with the screw through a feather key. When the system works, the motor drives the gear shaft to turn through Z2 geared with Z1. Therefore, when the larger gear runs clockwise or anticlockwise, the lead screw will move up or down correspondingly.

The open-loop transfer function of a stroke regulation system of metering pump is derived as follows according to literature [16]:

Equation (1) is rewritten as the following observable canonical form

Substituting the above formula into Eq. (2) gives

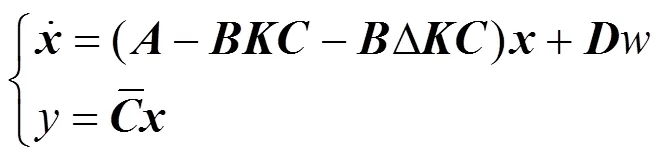
3 ROBUST NON-FRAGILE PID CONTROLLER DESIGN

Lemma 2 [19] For the linear system

Remark 2 For most of slow processes such as flow rate, temperature, pressure., we can find the corresponding positive-definite symmetric matrixthrough solving the above Riccati inequality.

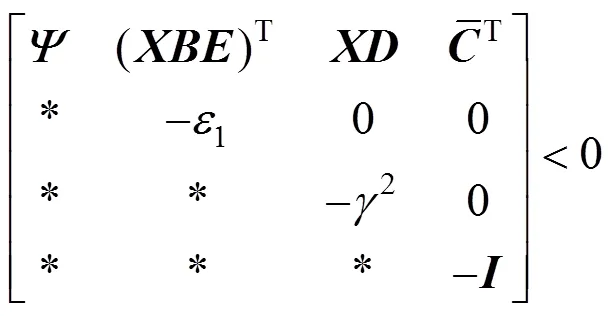
and

where

and the controller parameter is

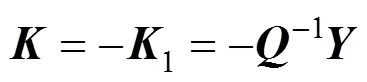
where

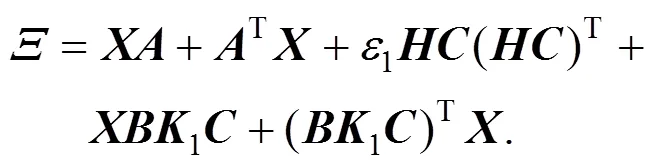
Let

since the matrixis full column rank, the columns ofandare all linearly independent with>0. Therefore

which implies that the matrixmust be nonsingular.

Theorem 2 Given a disturbance attenuation index, the controller parametercan be expressed as

Thus, Eq. (10) is obtained from Eqs. (8) and (11), andis obtained according to Theorem 1.

The whole design flow chart of a controller is given in Fig. 2.

4 ILLUSTRATIVE CASE

This section demonstrates the effectiveness and applicability of the proposed method. A three-phase hybrid stepping motor is used in this system. According to Eq. (1), the system is of two orders. In order to get a more precise model and overcome the adverse influence of non-model errors, the model parameters are identified by least square (LS) algorithm based on step response data (the identified algorithm is omitted due to limited space and the details are given in literature [2]). Hence, the system open-loop transfer function is

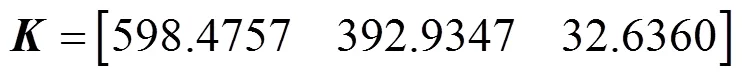
The corresponding controller parameters by using the Ziegler-Nichols tuning method are

For the given reference output or set point equaling 1.0, the corresponding outputs of the closed control system are shown in Figs. 3-5.

Figure 2 Design flow chart of a controller

Figure 4 Outputs of the closed control system with the proposed method for Δ1, Δ2and Δ3

Figure 5 Outputs of the closed control system with the Z-N method for Δ1, Δ2and Δ3

Figure 3 illustrates the outputs of the closed-loop system with the PID controller obtained with the proposedapproach and the traditional Z-N method. The output has smaller overshoot and shorter regulating time with the proposed method.

Figure 4 expresses the outputs of the closed-loop system by the controller obtained with this job subjectedto three kinds of perturbation. Although both the overshoot and the regulating time are increased slightly due to the perturbations Δ2and Δ3, the output can quickly return to its stet point. Fig. 5 shows the outputs of the closed-loop system with the controller obtained by the Z-N method for the above three kinds of perturbation. The overshoot and the regulating time are obviously increased for the given perturbations Δ2and Δ3in comparison with Fig. 4.

The simulation shows that the non-fragile PID controller has strong perturbation rejection performance, thus the gain perturbation has smaller influence on the system response compared with the Z-N tuned controller. With or without gain perturbation, the system response can achieve the steady state in a short regulating time.

5 CONCLUSIONS

The main task of metering pump stroke regulation is to make the system output reach the given set point as accurately as possible and quickly response to its change. This work discusses the design of a robust non-fragile PID controller focusing on stroke regulation of metering pumps with controller uncertainties. The sufficient conditions for a non-fragile controller with additive uncertainties are derived. When the conditions are feasible, the explicit expressions of a desired controller are given. The simulation results validate the feasibility of the modeling method and the robustness of the non-fragile controller.

NOMENCLATURE

ttransient hydra-dynamic damping coefficient

vviscous friction coefficient of the sliding key

deviation between a reference output and real output

() transfer function in a complex variable

unit matrix

1moment of inertia of the smaller gear shaft

2moment of inertia of the larger gear shaft

PID controller parameter vector

mtorsional stiffness of a motor shaft

sstiffness coefficient of a screw

Δbound vector of additive perturbation of a controller gain

screw length

screw mass

Ttranspose matrix of

-1inverse matrix of

reference input

output of the controller (control action)

zero-mean Gaussian white noise unrelated with initial state

system output

1, Z2 smaller and larger gears

1,2number of teeth of the smaller and larger gears

motor stepping angle

given disturbance attenuation index

:= defined as

* block matrix that is symmetric about principal diagonal

1 Sun, L., Helen H.L., “A strategy for multi-objective optimization under uncertainty in chemical process design”,...., 16 (1), 39-42 (2008).

2 Yu, S.M., Wang, H.Q., “Improved generalized predictive control algorithm with offline and online identification and its application to fixed bed reactor”,...., 11 (1), 49-54 (2003).

3 Zhang, W.Y., Huang, D.X., Wang, Y.D., Wang, J.C., “Adaptive state feedback predictive control and expert control for a delayed coking furnace”,...., 16 (4), 590-598 (2008).

4 Hou, W.F., Su, H.Y., Mu, S.J., Chu, J., “Multi objective optimization of the industrial naphtha catalytic reforming process”,...., 15 (1), 75-80 (2007).

5 Wang, Z.H., Chen, Z.Q., Sun, Q.L., Yuan, Z.Z., “Multivariable decoupling predictive control based on QFT theory and application in CSTR chemical process”,...., 14 (6), 765-769 (2006).

6 Cao, Q., “Development and application of metering pumps”, Petro- chemical Equipment, 30 (5), 44-47 (2001). (in Chinese)

7 Mimmi, G., Pennacchi, P., “Diaphragm design improvement for a metering pump”,, 8 (1), 1-13 (2001).

8 Rajendran, S., “Considerations in design of metering pump systems”,, 30 (5), 87-91 (1995).

9 Day, T.J., “Metering pump optimization to reduce operating costs”,, 48 (4), 20-22 (2008).

10 Wang, L.F., Wang, G.W., “Research on microchip controlled metering pump flow system”, In: 5th International Conference on e-Engineeringand Digital Enterprise Technology, Guiyang, China (2006). (in Chinese)

11 Martin, S., Vladimir, H., Lstvan, S., “Development of control system for fuel metering pump”, In: Proceedings of 35th Annual Conference of the IEEE Industrial Electronics Society, Porto, Portugal (2009).

12 Yao, B., Wang, F., “LMI approach to reliable∞control of linear systems”,, 17 (2), 381-386 (2006). (in Chinese)

13 Lien, C.H., “∞non-fragile observer-based controls of dynamical systemsLMI optimization approach”,,, 34 (2), 428-436 (2007).

14 Park, J.H., “Robust non-fragile guaranteed cost control of uncertain large-scale systems with time-delays in subsystem interconnections”,, 35 (4), 233-241 (2004).

15 Di, H.T., Shao, J.P., Zheng, W.B., “The development of metric pump closed control system”,, 5 (10), 37-39 (2005). (in Chinese)

16 Gong, Y.T., Xiao, S.G., Song, M.M., “Dynamics modeling and simulation for flow control system of mechanical electrical and hydraulic integration”,, 11 (36), 73-75 (2008).

17 Li, H.J., Chen, M.J., “Design of∞robust PID controller based on LMI”,, 3 (14), 294-296 (2007). (in Chinese)

18 Carlos, E., Souza, D.E., Xi, L., “Delay-dependent∞robust control of uncertain linear state-delayed systems”,, 35 (9), 1313-1321 (1999).

19 Wang, Y.J., Shieh, L.S., “Observer-based robust∞control laws for uncertain linear systems”,,, 14 (6), 741-751 (1991).

20 Ho, D.W.C., Lu, G.P., “Robust stabilization for a class of discrete- time nonlinear systemsoutput feedback: The unified LMI approach”,, 76 (2), 105-115 (2003).

** To whom correspondence should be addressed. E-mail: ysm@zjut.edu.cn

2010-02-08,

2010-08-31.

the National Natural Science Foundation of China (60604015) and the Key Research Program of Education Department of Zhejiang Province (Z200803521).