基于非抽样Contourlet变换的图像增强

罗红艳

(苏州工业职业技术学院，江苏苏州215104)

0 引言

小波变换理论与方法因其独特的时(空)—频多尺度分析技术，近年来在图像处理领域已得到广泛的应用。然而，由一维小波拓展为二维小波虽然能有效表示含“点奇异”的二维函数，但对于含“线奇异”的信号，虽然在逼近性能上要优于三角基，却也不能达到理想的最优逼近阶。

为了有效克服小波变换在图像去噪［1］方面的不足，人们将目光转向了新型奇异性分析工具。脊波(Ridgelet)变换、曲波(Curvelet)变换和轮廓(Contourlet)变换正是为解决二维或更高维奇异性而出现的新型分析工具。遗憾的是Randon变换的存在决定了脊波和曲波的计算复杂度和冗余度都很高，大大限制了其在图像去噪领域的应用。轮廓变换［2］是M.N.Do和Martin Vetterli提出的一种“真”二维图像表示方法，它不但具有小波分析的多尺度、时频局部化和临界采样特性，而且还具有多方向性和各向异性，能有效地捕获到自然图像中的轮廓，并对其进行稀疏表示，从而提供了一种快速的、结构化的分解采样信号方法，很好地克服了小波变换的缺陷，是近年来图像增强领域的研究热点。

然而，轮廓变换是在离散域内进行的，采样操作使其丧失了平移不变性，从而导致图像去噪时奇异点周围存在伪吉布斯(Gibbs)现象。以非下采样金字塔分解及非下采样方向滤波器组为基础，Cunha等人改进了Contourlet变换，提出了非下采样 Contourlet变换(Nonsubsampled Contourle Transform，NSCT变换)［3］。与轮廓变换相比，NSCT不仅具有完全平移不变性、而且具有良好的频率选择性和正则性，非常适合图像去噪与恢复。

本文以非下采样轮廓变换为基础，提出了一种新的图像去噪方法，首先对含噪图像进行非下采样轮廓变换，然后采用自适应阈值对变换系数进行处理，最后重构回原图像。

1 非下采样NSCT变换

轮廓变换是通过塔形方向滤波器组(PDFB)把图像分解成各个尺度上的带通方向子带，主要由两个步骤实现:子带分解和方向变换。首先，用Laplacian(LP)金字塔分解对图像进行多尺度分解，以“捕获”奇异点，然后由方向滤波器组(DFB)将分布在同方向上的奇异点合成为一个系数。非下采样Contourlet变换(NSCT，nonsubsampled contourlet transform)是 Contourlet变换去掉了下采样部分，构造相应的分级和各种方向滤波器得到的。图1为NSCT总体结构图，由非下采样金字塔滤波器组将图像分解为低频部分和高频部分，然后由非下采样方向滤波器组将高频部分分解为若干个方向。显然，非下采NSCT变换是一种完全时不变、多尺度、多方向的扩展，能快速实现。在滤波器的设计问题上受到的限制比contourlet变换要少，这使得我们在子波分解时能具有更好的频率选择性。NSCT已经被证实在进行图像去噪和增强时十分有效。

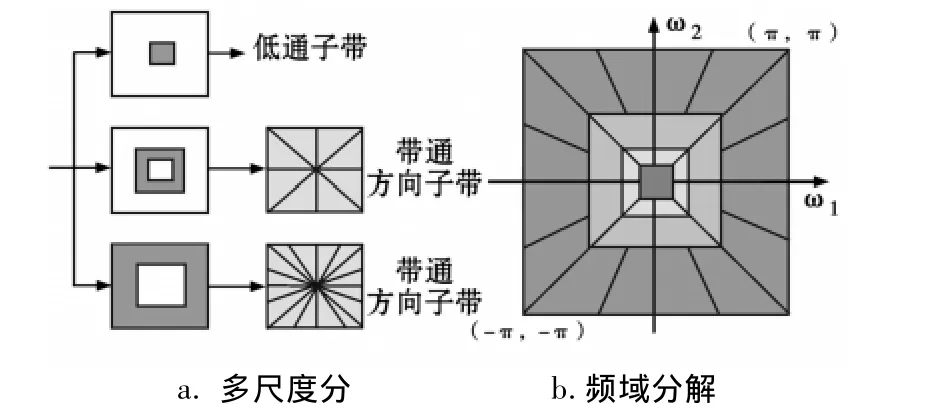
图1 NSCT结构图(a)非下采样滤波器 (b)理想频率

1.1 非下采样金字塔滤波器组

非下采样金字塔结构是通过多级迭代的方式实现的。首先提供满足下列完全重建条件一组基本的低通、高通滤波器组

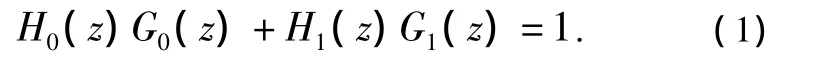
其中:H0(z)为低通分解滤波器，H1(z)为高通分解滤波器;G0(z)为低通重建滤波器，G1(z)为高通重建滤波器。

2 基于非下采样轮廓变换的自适应阈值图像去噪

图像增强技术通常有两种方法:空间域法和频率域法。使用NSCT对图像进行增强处理显然属于后者。

在图像去噪中，一般假设原始图像被均值为零、方差为σ2的加性平稳高斯白噪声所污染，则含噪声图像在非下采样轮廓变换域可表示为:

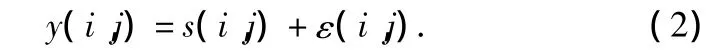
其中，s(i，j)和ε(i，j)分别表示原始图像和噪声的非下采样轮廓变换系数。

阈值去噪是一种实现简单而效果较好的非线性去噪方法，其优点是噪声可以得到很好的抑制，且反映原始特征的尖峰点得到很好保留。最早的阈值去噪方法是Donoho提出的VisuShrink方法，又称为通用阈值去噪法。该方法认为，信号对应的小波系数包含有信号的重要信息，其幅值较大，但数目较少，而噪声对应的小波系数是一致分布的，个数较多，但幅值小。

基于这一思想，Donoho等人提出软阈值和硬阈值去噪方法［4］。即寻找一合适的数T作为阈值，把低于T的小波系数设为零，而对高于T的系数，则予以保留或进行收缩，从而得到估计小波系数，然后进行重构。

VisuShrink阈值公式如下:

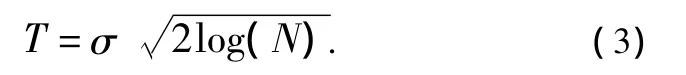
其中N代表信号的长度，σ代表高斯噪声方差。

在频率域，弱边缘和噪声都表现为较小的变换系数。所以，图像增强算法中好的阈值和增强函数必须在增强弱边缘的同时，对噪声进行有效地抑制。如果对不同尺度不同方向上的变换系数采用同样的阈值，那么对一处噪声的抑制可能会对另一处的噪声进行了增强［5］。为了避免这种情况，本文采用变换系数自适应地确定阈值。

设定阈值Tkl与变换系数的标准差成正比，即

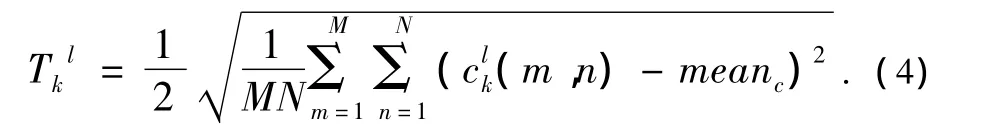
本文提出的自适应增强算法可以在不同尺度和不同方向上自适应地选取不同的阈值，对弱边缘进行放大，同时遏制噪声，具体算法步骤为:

(1)对待处理图像进行N层NSCT变换，得到不同尺度不同方向上的变换系数。

(2)对不同的变换系数，根据公式确定阈值T，使用硬阈值方法对系数进行处理，即小于T的系数置零。

(3)对处理后的变换系数进行反变换，实现图像增强。

3 仿真实验

选取512×512×8bit标准灰度图像Barbara叠加均值为零的白噪声进行实验。高斯白噪声方差为40，并与小波域去噪方法、轮廓变换域去噪方法进行了对比。实验中，小波域去噪采用了“db8”小波对图像进行三层小波分解;轮廓变换域去噪选择了“9－7”塔式分解和方向滤波器组进行三层分解，方向数分别为4，8，8;非下采样轮廓变换域去噪所采用的分解级数为三级，方向数分别为4，8，8。

实验结果见图2。

图2 实验结果

4 总结

通过以上理论分析及实验验证可以看出，采用NSCT去噪取得了较好的效果。去噪后，运用小波变换图像偏暗，对比度差，而CT去噪后轮廓变得不够清晰，这是因为其不具有平移不变形，产生了伪吉布斯现象。

［1］Donoho D L.De-noising by Soft-thresholding ［J］.IEEE Trans.on Inform.Theory，1995，41(3):613 －627.

［2］Do M N，Vetterli M.The Contourlet Transform:Anefficient Directional Multiresolution Image Representation［J］.IEEE Trans.on Image Processing，2005，14(12):2091 －2106.

［3］Cunha A L，Zhou J，Do M N.The Nonsubsampled Contourlet Transform:Theory，Design and Applications［J］.IEEE Trans.on Image Processing，2006，15(10):3089 －3101.

［4］Do M N.Contourlet Toolbox［OL］.http://www.ifp.uiuc.edu/～ minhdo/software/.2007，10.

［5］Sendur L，Selesnick I W.Bivariate Shrinkage Functions for Wavelet-based Denoising Exploiting Interscale Dependency［J］.IEEE Trans.on Signal Proc.，2002，50(11):2744－2756.