基于模糊PID的风电系统转速控制仿真研究

赵辉，李斌，朱利强，刘俊杰

(1.天津市复杂控制理论与应用重点实验室(天津理工大学)，天津300384;2.河北省石家庄供电公司，河北石家庄050061)

变速恒频风力发电系统是当今世界风力发电技术的主要方向。风力发电系统运行于额定风速以下和以上时，分别有不同的控制策略。当其运行于额定风速以下时，要求风轮的转速随风速变化并保持恒定的最优叶尖速比，实现最大风能捕获。运行在额定风速以上时，通常采用变桨距控制技术保证输出功率平稳[1-3]。

由于风速变化的随机性以及风电机组的强非线性，要求风电控制系统响应快，超调小，控制精度高。文献[4]基于模糊规则切换的模糊PID-PID双模变桨距控制器，该控制器提高了转速控制的精度，具有一定的适应性和鲁棒性。模糊PID控制在调节桨距角体现其优越性。对额定风速以下转速的控制，文献[5]提出了采用模糊控制器改变发电机定子电压，依此调节发电机反力矩来改变转速，但系统抗扰动能力不强。文献[6]将模糊控制应用到风力机的转速控制中，实现了转速对参考值的跟踪，但系统稳态误差较大，难以达到较高的控制精度。

本文在模糊控制的基础上，设计了风力机转速模糊PID控制器，该控制器响应快，超调小，改善了风力机转速控制的动态过程。通过搭建风力机的数学仿真模型，分析风力机各项参数的关系。采用模糊PID控制器调节发电机定子电压，依此改变发电机反力矩来改变转速。仿真表明，该控制器能够明显缩短调节时间，改善了风力机转速控制的动态过程，具有较理想的控制效果。

1 风力发电机组的数学模型

根据贝兹理论，风力机捕捉风力实际能得到的有用功率输出是

式中，ρ为空气密度，kg/m3；A为风轮旋转一周所扫过的面积，m2；CP为风能利用系数；v为风速，m/s。

在风速一定的情况下，风力机捕获的有用功率P的大小取决于风能利用系数CP,而CP是叶尖速比λ和桨距角β的非线性函数，即

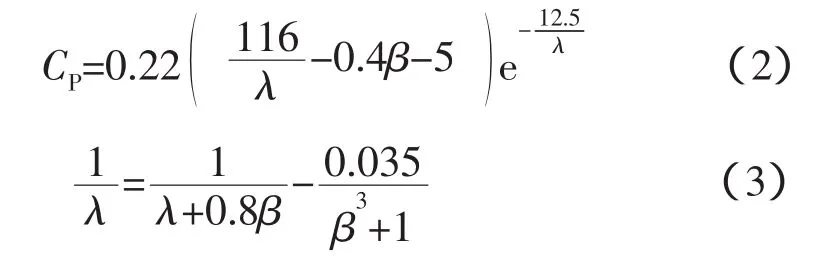
通过数学工具MATLAB，由式（2）和（3）可得到如图1的CP(λ,β)函数关系曲线。在额定风速以下，为了最大限度捕获风能，桨距角一般取恒值，即β=0°。根据贝兹理论，风能利用系数的极限值约为0.593。

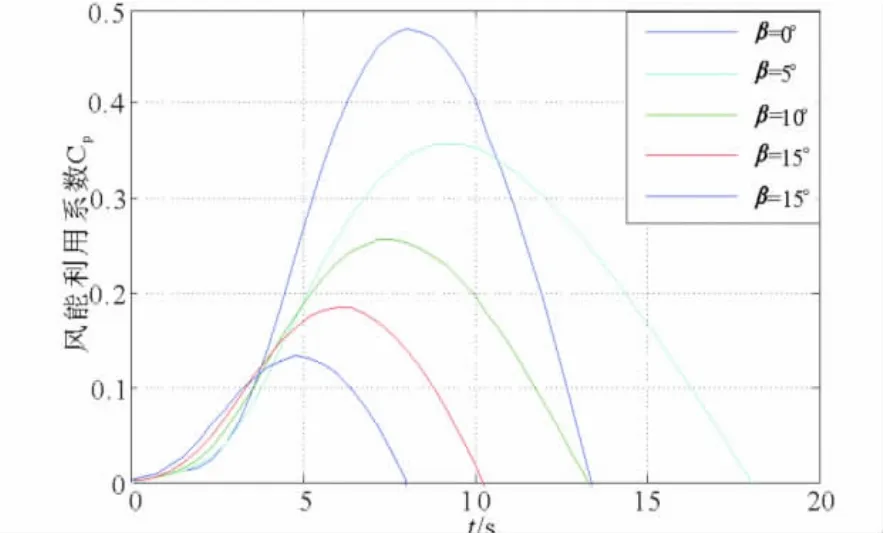
图1 风力机风能系数C P(λ,β)特性曲线

忽略风力机摩擦阻力，风力发电机组传动系统经过抽象后，其传动模型为

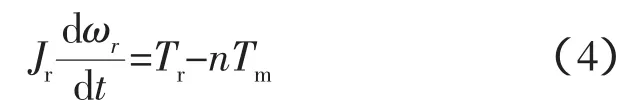
式中，Jr为风轮转动惯量，kgm2；ωr为风轮角速度，rad/s;Tr为风轮气动转矩，Nm；n为增速箱传动比；Tm为从转动轴传递给刚性齿轮的扭矩，Nm。

风轮与功率的关系为

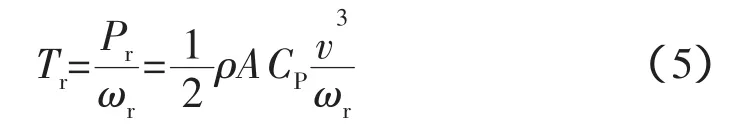
绕线式三相异步电机反力矩

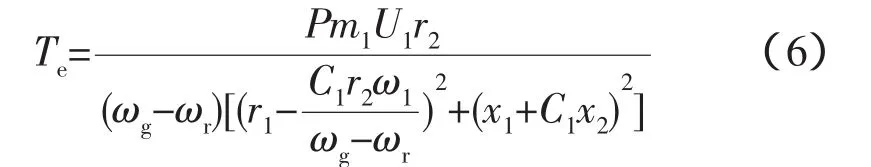
发电机转动方程为

p为发电机极对数；m1为电机定子相数；U1为定子电压；C1为修正系数；ωg为发电机角速度；ω1为发电机同步转速；r1，x1为定子绕组的电阻和漏抗；r2，x2为归算后的转子绕组和漏抗；Jg为发电机转动惯量；Te为发电机反力矩。

2 模糊PID控制器

模糊自适应PID控制指的是模糊技术与常规的PID控制算法相结合的一种控制方法。模糊控制器本身消除系统稳态误差的性能比较差，难以达到较高的控制精度；而PID调节器的积分调节作用从理论上可使系统的稳态误差控制为零，有很好的消除误差作用。因此把模糊控制和PID调节器相结合以增加稳态控制性能。

风速的随机性，要求系统的响应快，超调小。本设计的模糊自适应PID控制器的输入量为叶尖速比的误差E=9-λout和误差变化率ΔE，输出量为发电机定子电压的变化量。PID控制器三个参数的变化量Δkp，Δki和Δkd，分别加上PID控制参数的初始值，得到实际PID控制参数。模糊自适应PID控制器原理如图2所示。

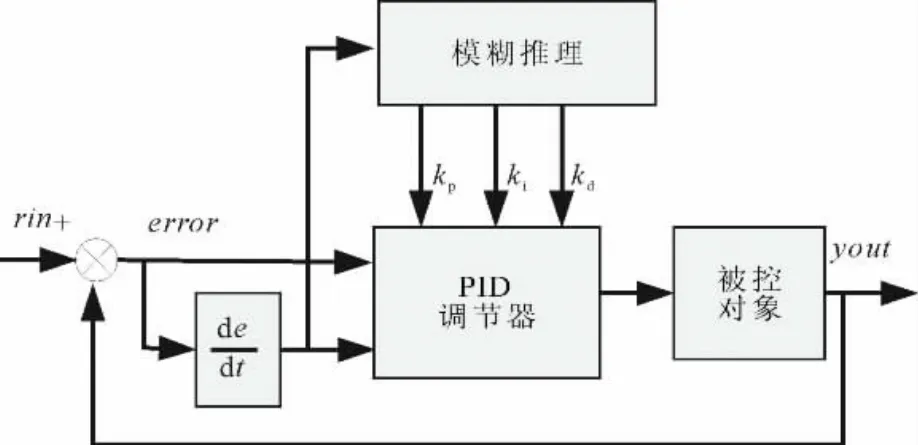
图2 模糊PID控制器结构图

kp，ki，kd的自适应校正将系统误差E和误差变化率ΔE变化范围定义为模糊集上的论域{E，ΔE}=[-5，-4，-3，-2，-1，0，1，2，3，4，5]，其模糊子集为{E，ΔE}={NB，NM，NS，ZO，PS，PM，PB}，子集中元素分别代表负大，负中，负小，零，正小，正中，正大。总结工程设计人员的技术知识和实际操作经验，建立了模糊PID规则表，如表1所示。

设E，ΔE和kp，ki，kd均服从正态分布，因此可得出各模糊子集的隶属度，根据各模糊子集的隶属度赋值表和各参数模糊控制模型，应用模糊合成推理设计PID参数的模糊矩阵表，修正参数代入下式计算：

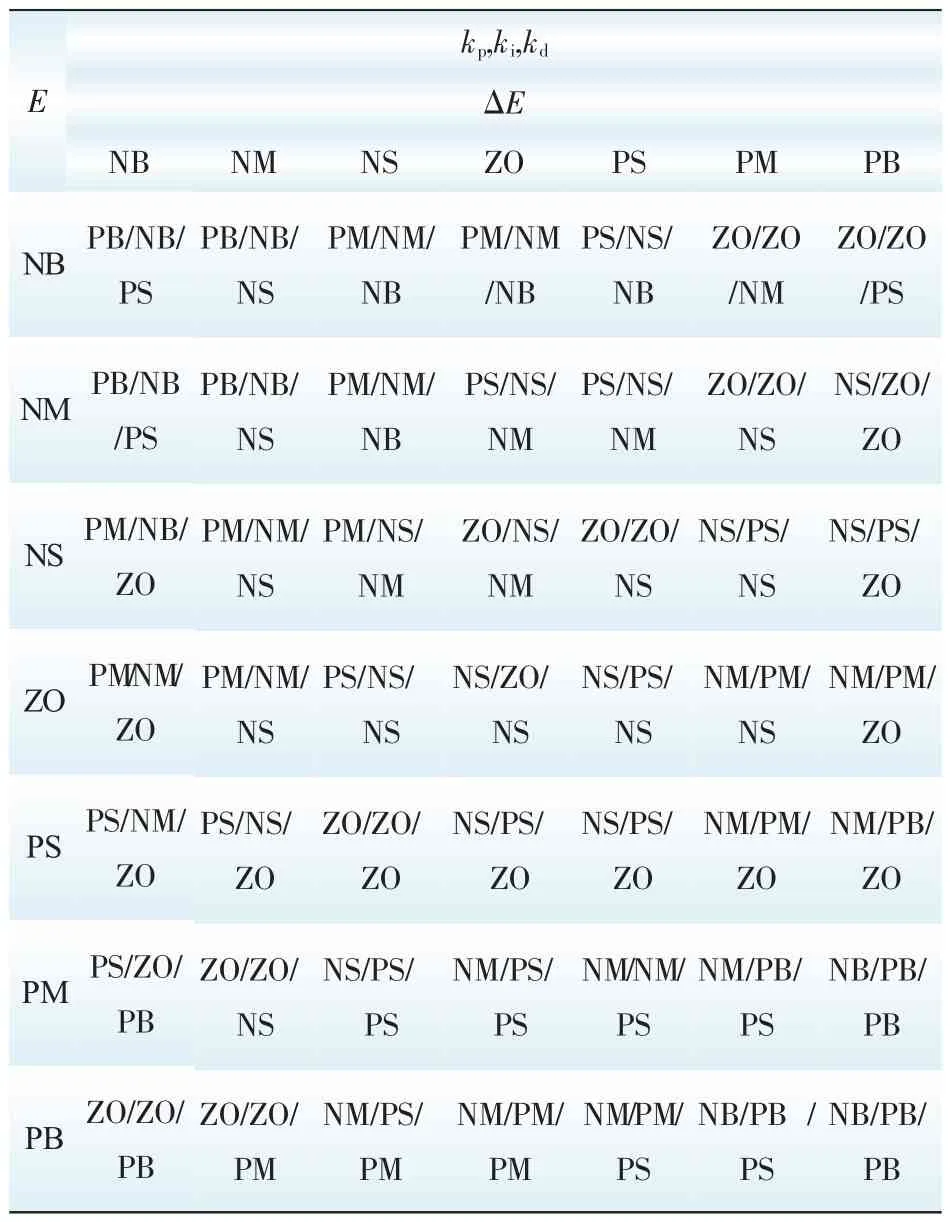
表1 模糊PID的k p，k i，k d的规则表

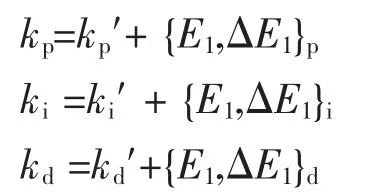
在线运行过程中，控制系统通过对模糊规则结果进行处理、查表和运算，完成对模糊PID参数的在线自校正。

3 仿真与结果分析

3.1 系统参数

本文采用的风力发电机组的相关参数为：风力机风轮转动惯量J r=2460106 kg·m2，直径R=62 m，风轮扫掠面积A=3848 m2，额定风速ve=13 m/s，切入风速vin=3.5m/s、切出风速vout=25m/s，额定功率P r=1.5 MW，空气密度取ρ=1.225 kg/m3。传动系统增速比n=78.9。

发电机转动惯量Jg=52kg·m2，额定功率Pg=1300 kW，额定转速vg=1522 r/min，定子相数m1=3，修正系数C1=0.811，定子额定相电压U1=690 V，定子绕组电阻及漏抗为r1=0.0109 Ω、x1=0.23 Ω。折算到定子侧的转子绕组及漏抗为r2=0.23 Ω、x2=0.18 Ω。

3.2 仿真分析

根据式（1）至（7），在Simulink中搭建风力发电机组仿真模型。仿真时间为20 s。额定风速下，桨距角置0°,取风速初始值为7 m/s。在10 s位置时风速发生突变至9 m/s，见图3。

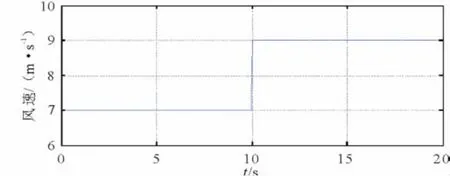
图3 风速变化曲线

风电系统在无控制器时，风力发电机组转速波动曲线。可以看出，风速为7 m/s时，该系统在6 s时达到稳定状态。在风速突变至9 m/s时，系统在4 s后达到稳定状态。该系统稳定时间过长，动态响应时间也不佳。系统亟需改进或加控制器，以捕获风能。仿真结果见图4。

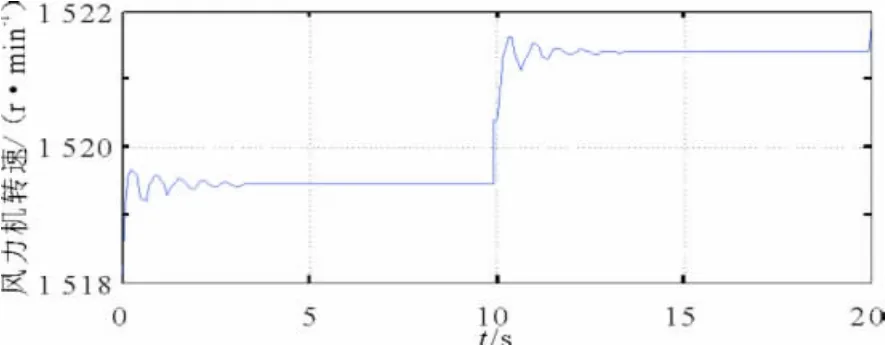
图4 无控制器风力机转速仿真结果

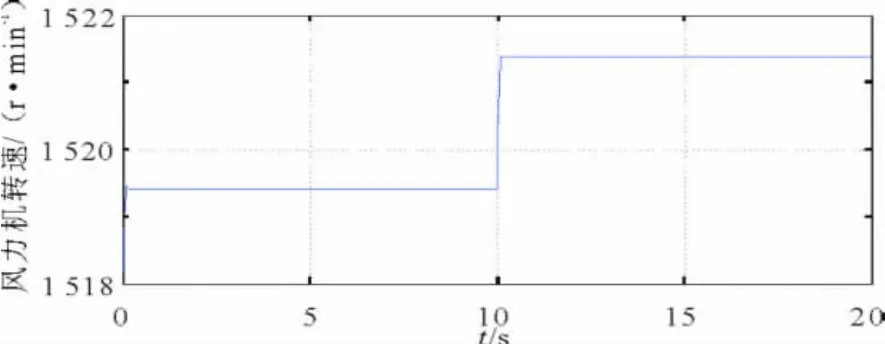
图5 PID控制器风力机转速仿真结果

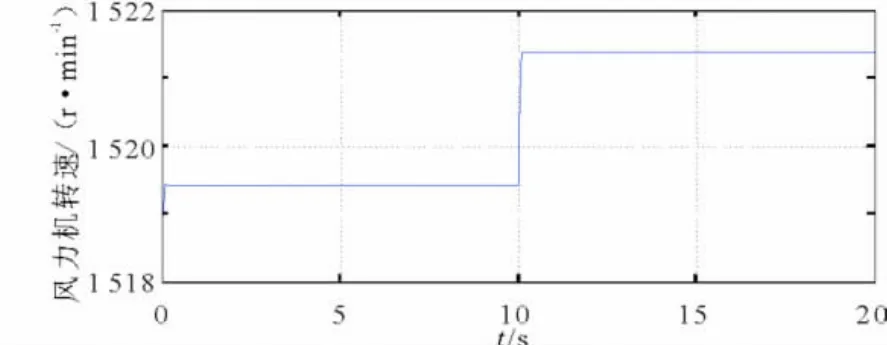
图6 模糊PID控制器风力机转速仿真结果

图5为PID控制时，风力机转速波动曲线。可以看出，系统的稳定时间明显缩短至0.9 s；在风速突变时，其动态性能不佳，有明显波动，而且风速突变后转速不稳定。图6为模糊PID控制时，风力机转速随时间变化曲线图，其稳定时间在0.9 s，控制效果与传统PID控制类似；而风速突变时，转速无明显波动。其动态响应效果较为理想。

4 结论

本文详细分析了风力发电系统的运行特性，将模糊PID控制策略引入风力发电机定子电压控制系统。采用MATLAB软件对1.5 MW风力发电机组的仿真表明模糊控制与PID控制相结合的模糊自适应PID控制，响应速度快，实时性高，取得了较好的控制效果。本文的工作有利于提高额定风速以下风力发电系统风能捕获的及时性与可靠性，实现系统的优化运行。

[1] 黄栋，李怀霞，张振.风电产业全球态势与政府政策[J].电网与清洁能源，2009,25(2)：46-49.

[2] 刘其辉,贺益康,赵仁德.变速恒频风力发电最大风能追踪控制[J].电力系统自动化,2003,27(20):62-67.

[3] 宋伟伟,李强,袁岳.双馈风电机组接入地区电网后的电压稳定分析[J].电网与清洁能源，2009，25(5)：36-40.

[4] 赵永祥，夏长亮.变速恒频风力发电系统风机转速非线性PID控制[J].中国电机工程学报，2008，11(28)：133-138.

[5] PRATS MAM，CARRASCO J M，GALVAN E，et al.Improving Transition Between Power Optimization and Power Limitation of Variable Speed Variable Pitch Wind Turbines Using Fuzzy Control Techniques[C].IECON26th Annual Conference of the IEEE，Nagoya，Aichi，Japan，2000.

[6] 沙非,马成廉,刘闯,等.变速恒频风力发电系统及其控制技术研究[J].电网与清洁能源，2009，25(1)：44-47.

[7] ZHANGX,WANGW,LIUY.Fuzzy Control of Variable Speed Wind Turbine[C].inProc.6th World Congresson Intelligent C-ontrol and Automation.Dalian,China,2006：3872-3876.

[8] ZHANG Xian-yong,SHU Jie,WU Chang-hong.A Novel Maximum Wind Power Capture Strategy For The Doubly-Fed Induction Generator[C].Power and Energy Engineering Conference,2009.APPEEC.Asia-Pacific 2009:1-4.

[9] 张纯明，姚兴佳，张忠丛.模型参考自适应电动变桨距控制[J].控制理论与应用，2008，25(1)：148-150.

[10] 牛志刚，张建民.应用于直线电机的平滑切换模糊PID控制方法[J].中国电机工程学报，2006，26(8)：132-136.