基于自适应小波变换的红外图像去噪算法
2011-05-10曹斌芳李建奇郭杰荣刘长青
曹斌芳, 李建奇, 郭杰荣, 刘长青
基于自适应小波变换的红外图像去噪算法
曹斌芳1, 李建奇2, 郭杰荣1, 刘长青1
(1. 湖南文理学院 物理与电子科学学院, 湖南 常德, 415000; 2. 湖南文理学院 电气与信息工程学院, 湖南 常德, 415000)
针对红外图像存在的加性、乘性及混合噪声, 提出了一种自适应小波变换的图像去噪算法. 该方法首先用小波变换对含噪图像信号进行小波分解, 这样可以保证对图像中的不相关噪声的有效抑制, 保持图像的细节信息. 然后将经小波变换所分离出来的噪声成分作为自适应滤波器的输入, 通过选用自适应滤波算法从而实现信噪分离的最佳滤波. 仿真结果表明, 本文提出的去噪算法优于已有的各种算法, 提高了图像的对比度, 突出了图像细节.
红外图像; 小波变换; 维纳滤波
红外线热成像是一种非接触无损伤式的体表温度测量方法. 它利用红外辐射成像的原理研究人体表面温度. 根据体表不同的温度分布以形成不同灰度像素点的图像. 这种图像噪声产生的因素主要是因为红外光波的相干作用, 既包括乘性噪声, 也包括加性噪声, 但大部分情形下加性噪声对图像的影响远小于乘性噪声的影响. 因此, 如果仍然使用传统的图像去噪算法, 将不能达到最佳效果. 针对这个情况, 文献[1]提出了一种基于小波变化的方法, 该方法将乘性噪声转换为加性噪声再处理, 但此转换方法存在较大的误差. 本文在此基础上提出了一种新的方法.
本文提出了一种红外图像的自适应小波去噪算法, 该方法首先用小波变换对含噪图像信号进行小波分解, 这样可以保证对图像中的不相关噪声的有效抑制, 保持图像的细节信息. 然后将经小波变换所分离出来的噪声成分作为自适应滤波器的输入, 通过选用自适应滤波器的维纳滤波算法从而实现信噪分离的最佳滤波, 以保证去除信号中的相关乘性噪声.
1 红外图像噪声类型及去噪分析
1.1 1/f噪声
1925年, 约翰逊在电子管板极电流中首次发现了1/噪声. 随后, 各种半导体器件中, 也发现此种噪声. 从20世纪50年代中期以来, 在真空管、二极管和晶体管的电压或电流中, 以及拾音器、半导体、金属薄膜的电阻中都发现了1/噪声[2]. 1/噪声是统计自相似的随机过程, 频率与功率谱密度成反比, 可见1/噪声在不同时刻取值是相关的. 在图像处理中, 为了去除1/噪声, 可利用小波变换的去相关作用, 合理地选择小波基, 使1/噪声变为易于清除的白噪声, 从而达到去噪的目的.
1.2 散斑噪声
在红外图像的成像过程中, 广泛的存在着散斑噪声, 它的形成主要是因为成像过程中红外波的相干涉作用, 除此以外, 它还与成像组织表面的粗糙程度有着密切的关系. 从视觉角度看来, 这种噪声在图像中呈现斑点分布状. 根据散斑的密度可以将这种噪声分成3种类型, 从数学角度散斑噪声可以用广义分布来描述.
从噪声的性质来分析, 严格地讲, 散斑噪声既包含乘性噪声的成分也包含加性噪声的成分, 可以由式(1)来表达:
=·m+a. (1)
式中为原始信号,m为乘性噪声信号,a为加性噪声信号,为含噪信号.
但是, 大部分情形下, 加性噪声对图像的影响远小于乘性噪声的影响, 因此可以将加性噪声忽略掉, 认为散斑噪声是一种乘性噪声.
1.3 噪声的分类
图像噪声按不同方法可以分成不同类别, 按噪声对信号的影响可分为加性噪声和乘性噪声两类. 设(,)为信号,(,)为噪声, 影响信号后的输出为(,).
a. 加性噪声:
(,) =(,) +(,). (2)
b. 乘性噪声:
(,) =(,)(1+(,))=(,)+(,)(,).(3)
其输出是两部分的叠加, 第二个噪声项信号受(,)的影响,(,)越大, 则第二项越大, 即噪声项受信号的调制. 如光量子噪声、底片颗粒噪声都随信号增大而增大. 乘性噪声模型和它的分析计算都比较复杂, 很多文献的分析都忽略了这种噪声, 但它对于红外图像处理将带来很大的误差.
2 本文采用的红外图像去噪方法
本文采用的红外图像去噪方法包含以下步骤: 首先用小波变换对含噪图像信号进行小波分解, 这样可以保证对图像中的不相关噪声的有效抑制, 保持图像的细节信息. 然后将经小波变换所分离出来的噪声成分作为自适应滤波器的输入. 通过选用自适应滤波器的维纳滤波算法从而实现信噪分离的最佳滤波, 以保证去除信号中的相关(乘性)噪声.
2.1 采用小波模极大值去除相关噪声
2.1.1 小波变换模极大值
在实际应用中, 为了减少计算的复杂度, 通常采用二进小波变换, 即只考虑二进尺度(= 2,ÎZ)的小波变换模极大. Mallat等人建立了小波变换与Lipschitz指数之间的关系[3-4]:
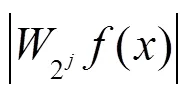

由式(4)可知, 对于一般的信号, 由于奇异指数³0, 小波变换的模极大值将随着的增大而增大; 而对于高斯白噪声(白噪声是指功率谱密度在整个频域内均匀分布的噪声),<0, 其模极大值随着的增大而减小. 因此, 根据不同尺度间小波变换模极大值变换的规律, 去除幅度随尺度的增加而减小的极值点, 保留幅度随尺度增加而增加的极值点, 再对保留的模极大值点进行重建, 可达到去噪的目的[5].
2.1.2 去噪步骤
a.对混有噪声的图像进行次小波分解, 得到各尺度上的小波变换系数, 并找出小波变换模极大值.
b.根据信号和噪声在小波变换各尺度上不同传播特性, 从尺度2上的模极大值序列开始, 在尺度2上各模极大值点的小邻域内向上, 寻找它的尺度2+1上的传播点. 依次进行下去, 由噪声对应的模极大值就基本去除了, 但在幅值较大的位置依然有一些残余噪声存在. 再对模极大值进行软阈值处理, 就得到一组新的模极大值点. 对新的模极大值点采用重构方法, 以便通过这些模极大值模拟出来的小波变换函数在给定点处具有模极大值. 由此得到的重构小波系数仅带有真实信号的信息, 噪声得到抑制.
c.利用MATLAB重构算法类型逆变换, 可得到去噪后的图像.
2.2 采用维纳法去除图像中的相关噪声
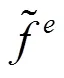
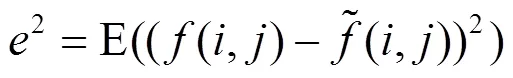


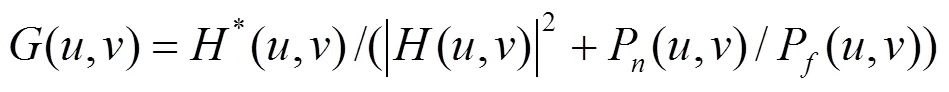




首先估计出像素的局部矩阵均值和方差:


是图像中每个像素的×邻域, 利用Wiener滤波器估计出其灰度值:
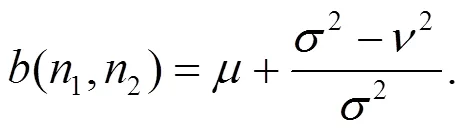
3 实验结果和分析
3.1 图像去噪效果的评价方法
图像去噪是为了消除图像中的噪声, 使去噪后的图像尽可能接近原始图像质量评价图像去噪效果的目的在于更好地认识算法的功能和不足. 一般来说, 评价去噪后的图像一般需要考虑三个方面的内容:噪声衰减程度、边缘保持程度、区域平滑程度. 理论上讲, 去噪后的图像应该尽可能地衰减噪声, 保持图像边缘鲜明, 尽可能地平滑区域. 简言之就是“去噪保鲜”. 评价图像去噪的方法可以分为两类: 主观评价法和客观评价法[9]. 本文采用如下的数字指标来客观评价去噪效果.
a. 图像的峰值信噪比(P, Peak Signal to Noise Ratio):


其中是图像中灰度的最大值, 对于256级的灰度图像,= 255.×是图像的大小,M为图像的均方差,(,)为实验原图像的灰度值,(,)是去噪后的图像的灰度值.
b. 图像相关系数(c):

其中,分别代表原图像和去噪后的图像, cov(,), var(), var()分别代表原图像的和去噪后的图像的协方差和方差. 给出这一指标主要是出于这样的考虑: 理想状态下, 被恢复的图像应该和原来的图像尽可能的接近, 而相关系数接近于1的程度就描绘了两幅图像的接近程度, 从整体上可以衡量图像被恢复的程度.
3.2 计算机模拟仿真结果与分析
实验中采用像素为256×256大小的红外图像作为原始图像, 加入均值为0, 方差大小为0.05的加性高斯噪声和均值为0, 方差为0.04的乘性噪声.
在信噪比固定情况下的仿真图见图1.

图1 各种算法的去噪红外图像
实验结果采用峰值信噪比(P)和相关系数c进行比较. 表1给出4种红外图像去噪前后P和c改善情况:

表1 4种红外图像去噪前后RP 和cc 改善情况
从图1的红外图像增强效果图和表1可以看出:
维纳滤波法、小波模极大值去噪方法和文献[1]的方法虽然也得到了比较清晰的图像, 但是在一些边缘处出现了明显的模糊现象; 峰值信噪比和相关系数也有较大的提高.
而本文提出的自适应小波去噪算法则能得到清晰边缘图像, 既能较好的去除乘性噪声, 消除图像和噪声的相关性, 同时也较好地去除了不相关的高斯噪声. 由表1可知, 本文突出的自适应小波去噪算法增强的图像P明显高于其它方法.
4 结论
传统的红外图像去噪算法没有很好地考虑乘性噪声对图像质量的影响, 在去除加性噪声的同时忽略了乘性噪声, 文献[1]提出了将乘性噪声转换为加性噪声进行噪声消除, 存在较大的转换误差, 本文在此基础上提出了一种红外图像自适应小波去噪算法, 既能很好地去除图像中的加性高斯噪声, 又能对乘性噪声做到较好的抑制. 无论是在视觉效果还是在图像的峰值信号比和相关性定量指标上均明显优于小波去噪法和文献[1]中的方法, 并充分保留了图像的细节信息.
[1] 张瑾, 陈向东. 一种基于小波变换的红外图像去噪方法[J]. 传感器与微系统, 2009, 25(8): 7-9.
[2] 冯贞, 马齐爽. 基于小波分析的红外图像非线性增强算法[J]. 激光与红外, 2010, 40(3): 315-318.
[3] 郭彤颖, 贺红莹, 袁峰,等. 基于小波模极大值的火灾图像边缘检测方法[J]. 沈阳建筑大学学报:自然科学版, 2010, 26(1): 201-204.
[4] 闫敬文, 屈小波. 超小波分析及应用[M]. 北京: 国防工业出版社, 2008.
[5] 许开宇, 李双一. 基于小波变换的图像融合算法的实现[J]. 红外技术, 2007, 29(8): 455-458.
[6] 安博文, 辉林如. 基于边缘检测的自适应降噪处理方法[J]. 红外技术, 2010, 32(3): 142-144.
[7] 杨鸿森. 基于总体最小二乘的红外图像去噪[J]. 激光与红外, 2008, 38(9): 961-964.
[8] Grau V, Raga M A, Monserrat C. Hierarchical image seg- mentation using a correspondence with a tree model [J]. Pattern Recognition, 2004, 37(1): 47-59.
[9] 潘泉, 张磊, 孟晋丽, 等. 小波滤波方法及应用[M]. 北京: 清华大学出版社, 2005.
Infrared image denoising algorithm based on adaptive wavelet transform
CAO Bin-fang1, LI Jian-qi2, GUO Jie-rong1, LIU Chang-qing1
(1. Department of Physics and Electronics, Hunan University of Arts and Sciences, Changde 415000, China; 2. Department of Electronic Engineering, Hunan University of Arts and Sciences, Changde 415000, China)
According to infrared images with additive, multiplicative, and mixed noise, this paper puts forward a infrared image denoise algorithm based on adaptive wavelet transform. First, noised infrared image signal is investigated using wavelet transform, additive noise is reduced so that infrared images detail is maintained, then the separated noise of signal by wavelet transform is the input signal of adaptive filter. The optimal filtering method of signal-noise decomposition is realized by filter algorithm and correlated noise of signal removaled is established. Simulation results show that the proposed denoising algorithm is better than many exiting methods , and solves the problem of the low contrast in infrared image, and highlights the image detail .
infrared image; wavelet transform; winner filter
10.3969/j.issn.1672-6146.2011.03.011
TN 911.73
1672-6146(2011)03-0037-04
2011-06-27
曹斌芳(1979-), 女, 讲师, 博士研究生, 研究方向为自适应滤波器、图像处理. E-mail: cao_bf@163.com
湖南省自然科学基金(11JJ6062); 湖南文理学院青年专项基金(YXQN1005)
(责任编校: 刘刚毅)
