带干扰的双险种复合二项负风险模型的破产概率
2011-05-10邓迎春郑敏衡白美保
邓迎春, 郑敏衡, 白美保
带干扰的双险种复合二项负风险模型的破产概率
邓迎春, 郑敏衡, 白美保
(湖南师范大学 数学与计算机科学学院, 湖南 长沙, 410081)
研究了索赔过程为复合二项过程的负风险模型, 利用鞅方法和相关的随机过程的知识, 以两种不同的方法得到了该模型的最终破产概率以及Lundberg不等式.
负风险; 复合二项过程; 布朗运动; 破产概率
依据保险公司理赔方式的不同, 风险模型可以分为正风险模型和负风险模型两大类. 经典负风险模型[1]定义为:

当理赔次数过程的均值大于方差时, 用理赔次数为泊松过程的负风险模型就不再合适了. 文献[6]考虑了索赔次数为复合Poisson-Geometric过程的情况, 文献[7]考虑了索赔次数为复合负二项过程的情况. 本文将进一步把该模型推广到带干扰的双险种复合二项负风险模型.
1 模型引入
2 主要结论

.



定理3 对于风险模型(2), 其最终破产概率为:

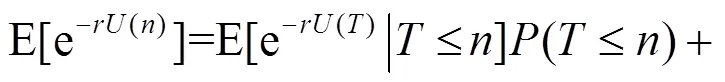

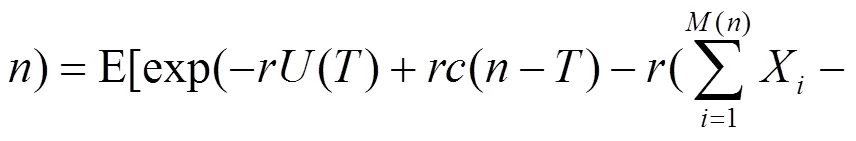

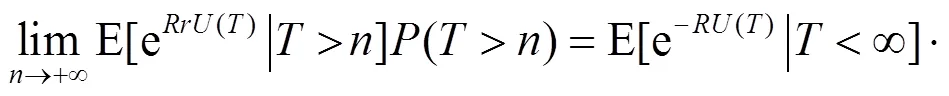

记




由契比雪夫不等式, 得:
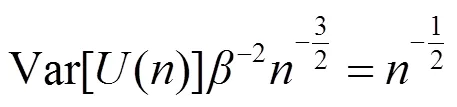
证明2 下面用鞅方法证明该定理.
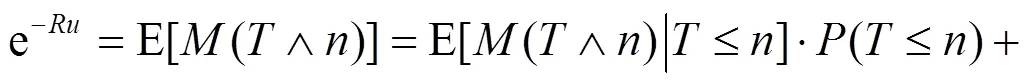





[1] Grandell J. A spects of Risk Theory[M]. New York: Springer-Verlag, 1991: 4-11.
[2] Wang Guojing, Wu Rong. Some distributions for classical process that is perturbed by diffusion[J]. Insurance Math Econom, 2000, 26(1): 15-24.
[3] Gerber H U. An extension of the renewl equation and its application in the collective theory of risk[J]. Scandinav-ian Actuarial Journal, 1970, 3(2): 205-210.
[4] 方大凡, 王汉兴. 多质负风险和[J]. 应用概率统计, 2003, 19(1): 65-70.
[5] 董迎辉, 王过京. 相关负风险和模型的破产概率[J]. 应用概率统计, 2004, 20(3): 301-306.
[6] 熊双平. 带干扰的索赔次数为复合Poisson-Geometric过程的负风险和模型[J]. 经济数学, 2007, 24(1): 37-41.
[7] 郑敏衡, 邓迎春. 负二项过程下负风险模型的破产概率[J]. 湖南文理学院学报: 自然科学版, 2011, 23(2): 16-18.
Ruin probability in negative risk model with two compound binomial processes by diffusion
DENG Ying-chun, ZHENG Min-heng, BAI Mei-bao
(College of Mathematics and Computer Science, Hunan Normal University, Changsha 410081, China)
The paper considers the negative risk model perturbed by diffusion with aggregate claims modeled as two compound binomial processes, and the ruin probability are derived by martingale method.
negative risk; compound binomial process; Brown motion; ruin probability
10.3969/j.issn.1672-6146.2011.03.002
O 221.6
1672-6146(2011)03-0003-03
2011-06-06
邓迎春(1960-), 男, 教授, 研究方向为随机过程及其应用. E-mail: 734725037@qq.com
(责任编校: 刘晓霞)
