预应力钢筋混凝土风力发电塔架的地震响应分析

毕继红，任洪鹏，尹元彪

(1. 天津大学建筑工程学院，天津 300072；

2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072；

3. 新纪元综合咨询公司，东京 1250061)

当今全球面临的能源危机和环境问题促进了风能等可再生能源的大规模开发利用．为了实现我国风力发展的宏伟目标，宫靖远[1]详细介绍了风电场设计、风力发电机组的设计与制造、风电场建设施工等内容，并指出随着风力发电向单机大容量的发展，出现了钢筋混凝土塔架取代钢结构塔架的趋势. Singh[2]设计了一座高100,m的预应力钢筋混凝土塔架，指出此类塔架具有耐疲劳、稳定性能好、低维修和低造价等特点，适于建造在偏远地区或恶劣的环境中．Reinhard等[3]认为：塔高超过 85,m 时钢结构塔架将不能克服自身的振动激励作用；并以德国威廉港附近的一座功率为 3,MW、塔高 92,m 的预应力钢筋混凝土塔架为原型，考虑了预应力和风荷载的作用，对塔架结构进行了非线性分析．

地震荷载对高耸结构的破坏通常是非常严重的，且由于预应力钢筋混凝土塔架质量大，惯性力较大，对其抗震更为不利，故对风力发电塔架结构进行地震响应分析是很有必要的．Bazeos等[4]以450 kW的钢结构风力发电塔架为原型，建立了细化的有限元模型和简化的集中质量模型，比较分析了两种模型对于静态、稳定和地震响应的影响．Lavassas等[5]以 1,MW的钢结构风力发电塔架为原型，考虑了塔架和基础的耦合作用，对塔架进行了静态、疲劳和地震响应分析．李长风[6]建立了“桨叶-塔体-基础”一体化有限元模型，考虑了土和结构的相互作用，对风力发电塔架进行了模态分析和地震响应分析．Witcher[7]综合考虑了风的紊流作用和基础在发生地震时的震动作用，建立了气动弹性模型，运用GH Bladed风力发电机设计软件，研究了风力发电机在工作状态时的地震响应分析．

由于预应力钢筋混凝土风力发电塔架具有稳定性能好、抗腐蚀性能强、维修费用低、节约钢材和现场加工方便等优点，且随着风力发电机向单机大容量和海上风力发电发展的趋势，预应力钢筋混凝土塔架将有更为广阔的前景．相对于钢结构，混凝土高耸结构的抗震性能较差，为此，针对预应力钢筋混凝土塔架，笔者在地震响应分析中讨论了工作用洞口的设置对塔架结构抗震性能的影响，探讨了不同的地震波入射角时塔架结构的地震响应．结果表明，该塔架具有较好的抗震性能．

1 计算模型

计算模型为 2,MW 的预应力钢筋混凝土风力发电塔架，高 65,m，由 22个不同横截面积和不同壁厚的预制混凝土构件组成，采用后张法使得预应力钢筋和混凝土形成整体．该塔架参数如表1所示．

利用 ANSYS软件建立预应力钢筋混凝土风力发电塔架的有限元模型．塔架的实体部分使用 C80混凝土，采用Solid65单元来模拟，普通钢筋采用等效弹性模量的方法施加在混凝土单元上．塔架的预应力钢筋采用 Link8单元来模拟，截面尺寸为11.84,cm2，预应力钢筋的分布情况按高度不同分别为8～36根．采用线弹性的钢筋混凝土本构模型，未考虑材料非线性和几何非线性．预应力钢筋混凝土塔架的设计模型和有限元模型如图1和表2所示．

图1 预应力钢筋混凝土风力发电塔架模型Fig.1 Model of pre-stressed reinforced concrete windturbine tower

表1 预应力钢筋混凝土风力发电塔架模型参数Tab.1 Pre-stressed reinforced concrete wind-turbine tower model parameters

表2 预应力钢筋混凝土风力发电塔架尺寸Tab.2 Size of pre-stressed reinforced concrete wind-turbine tower

2 模态分析

大型风力发电机多使用柔性塔架，其一阶固有频率一般比较接近叶轮激励频率，而高阶固有频率远远大于叶轮激励频率，不会同叶轮发生共振；因此进行模态分析时主要考虑的是塔架的一阶固有频率．

由文献[8]知，风机有 3个浆叶，由于扫掠面上部和下部的平均风速不同，每转 1周塔架受激振动 3次．本文中 2,MW 风力发电机叶轮的标定工作转速为 16.6,r/min，频率为 0.277,Hz，则作用在塔身上的轴向推力的频率为0.831,Hz．采用上述塔架模型进行模态分析，结果如表3和图2和图3所示．

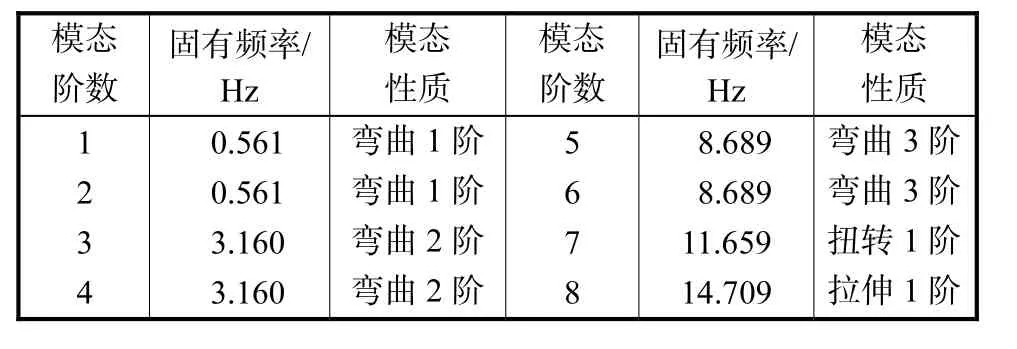
表3 塔架的模态计算结果Tab.3 Modal results of tower

由计算结果可见，塔架前两阶固有频率为 0.561 Hz，这是由于塔架在没有开洞的情况下，两个主方向的质量分布是相同的．前两阶模态的固有频率均在0.277～0.831,Hz的安全频率范围之内，故所设计的塔架为“柔塔”．

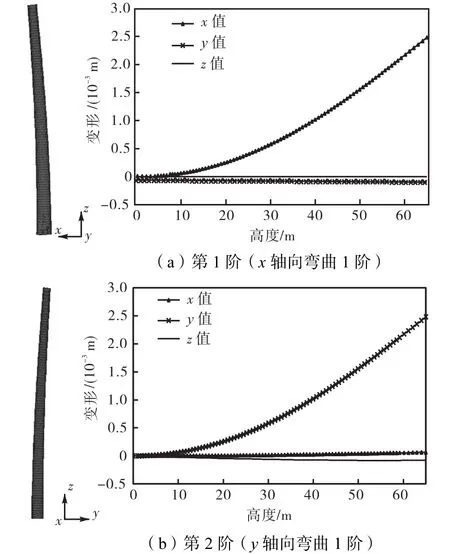
图2 塔架的振型(1～2阶)Fig.2 Vibration mode diagram of tower(1st and 2nd)

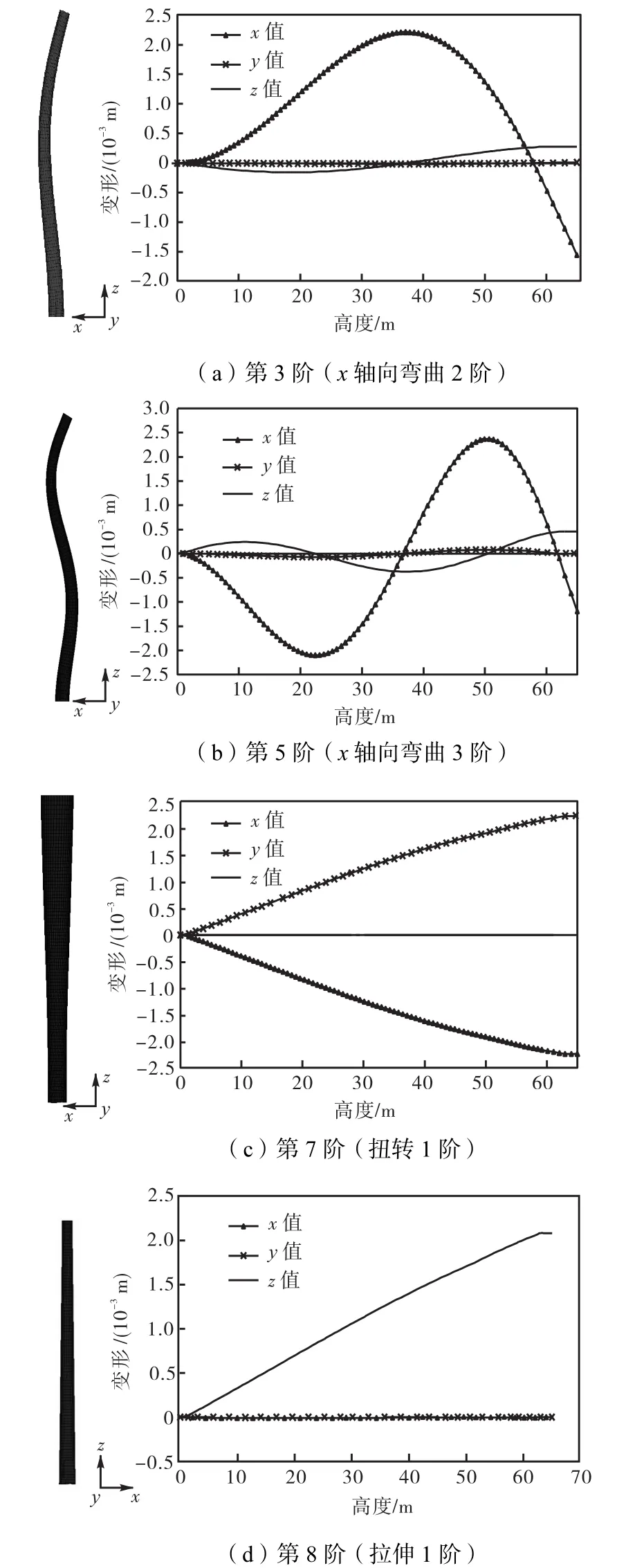
图3 塔架的振型(3～8阶)Fig.3 Vibration mode diagram of tower(3 rd—8 th)

3 地震响应分析

3.1 地震波的输入

在地震响应分析中，选取了认可度较高的 EL Centro波作为自由场地的基岩输入[9]，地震动输入时间间隔为 0.02,s，持续时间为 16,s，结构阻尼为ζs= 8 0%．未考虑地震波垂直分量对塔架结构的影响，具体方式是将地震波沿水平面的 2个主方向分解，然后施加在塔架结构上．

为便于将数值分析结果与规范的设计值进行比较分析，对预应力钢筋混凝土塔架的地震波输入乘以扩大系数 1.35，即输入地震波的幅值水平调整为2.43,m/s2．计算分析中，加速度幅值为 2.43,m/s2的 EL Centro波简记为EL2.43．图4所示为EL2.43波的时程曲线．图 5为 EL2.43波和日本土木学会设计指南[10]中选用的地震反应谱分析比较图，通过比较可以得出，2个波的频谱分析非常接近，表明本文采用调整后的EL Centro波进行时程分析，与日本土木学会设计指南提倡的设计地震强度是相近的．

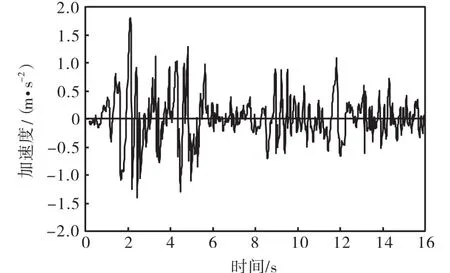
图4 EL2.43波加速度时程曲线Fig.4 Acceleration time-history curve of EL2.43

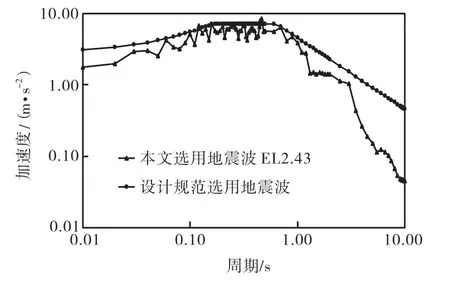
图5 EL2.43波与设计选用地震波的分析比较Fig.5 Comparison between EL2.43 and design code

3.2 未开洞塔架的地震响应分析

地震波为 EL2.43波．30节点位于距塔顶 1/3处，60节点位于距基底1/3处，而90节点位于塔架的基底以上0.7,m处．

图6是塔架不同高度处的位移时程分析图，可以看出，塔架顶端的位移幅值为 20,cm，同一塔架位置越高的点，水平位移越大；且各高度处节点的位移时程变化规律基本一致．图 7是塔架不同高度处的竖向应力时程分析图，从图中可以得出，塔架各高度处均未出现拉应力；同一塔架位置越低的点，竖向压应力值越大，在基底出现最大压应力 24,MPa，计算结果表明塔架截面按照变截面来设计是合理的．

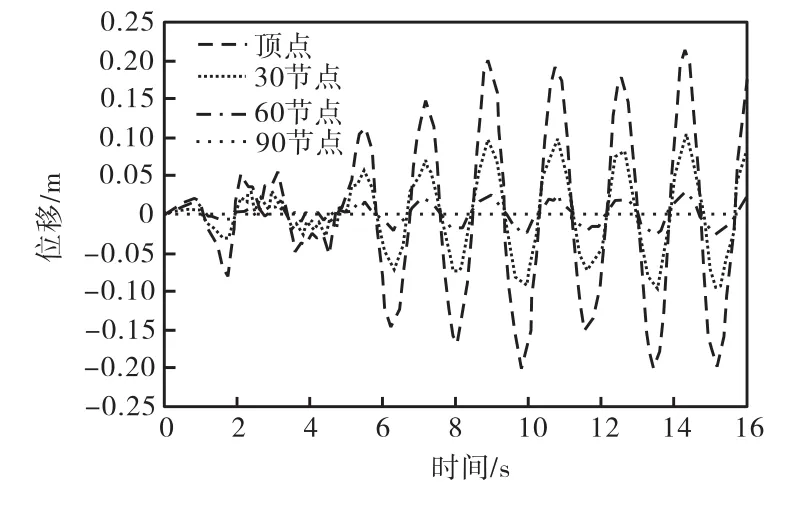
图6 塔架不同高度处的位移时程曲线Fig.6 Displacement time-history curves of tower at different heights

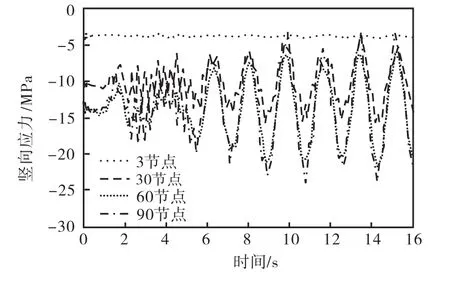
图7 塔架不同高度处的竖向应力时程曲线Fig.7 Vertical stress time-history curves of tower at different heights

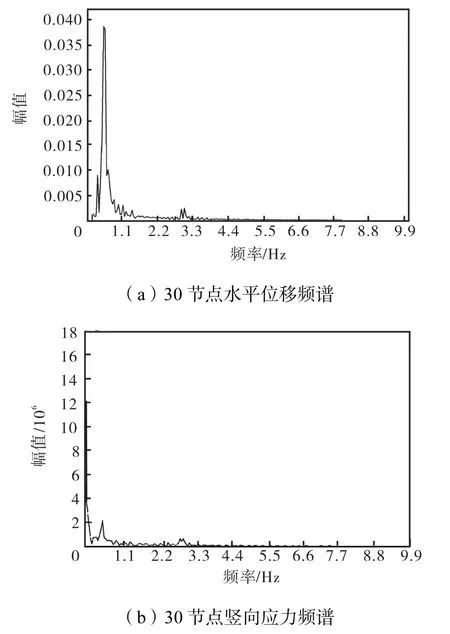
图8 塔架水平位移和竖向应力的频谱Fig.8 Horizontal displacement response spectrum and vertical stress response spectrum of tower

图8是塔架30节点处水平位移频谱图和竖向应力频谱图，从图中可以得出，30节点高度处的水平位移幅值和竖向应力幅值均发生在一阶固有频率处．地震波的施加也引起了塔架的高阶振型，但仍以一阶振型为主．

3.3 设计值与有限元值的比较

根据文献[10]，可以求出塔架各分部的竖向应力，并编制了优化塔架设计模型的excel表格，主要的设计参数如下所述．

(1)塔架剪力垂直方向的分布系数

式中：zi为截面的高度； H为塔架的高度．

(2)塔架弯矩垂直方向的分布系数

按照设计规范，地震时塔架各段截面内的剪力值与弯矩值为

式中：k0取值为α0/ g = 0 .184；Z为地震域系数，取值为1.0；Cb为基底传递系数，取值为1.029；W为塔架及轮毂的总重量；hg=H ( 0.934 + 0 .5Cs) /(1 + Cs) = 5 7.32．

(3)由塔架各段截面内的轴力、弯矩和预应力钢筋引起的竖向应力值为

式中：σp为考虑预应力损失后的预应力钢筋的张拉值，σp= 0 .9× 0 .85σy= 1 209 MPa ，其中σy= 1 581MPa；Ap为单根预应力钢筋的截面面积，Ap= 1 1.845cm2；ni为塔架各段截面内预应力钢筋的根数．

(4)不同塔架高度处，与地震波传入方向平行的塔架对称侧的竖向应力设计值为

通过有限元仿真分析，可以得到时间点 11.78,s时(最不利情况下)，不同塔架高度处，与地震波传入方向平行的塔架对称侧的竖向应力有限元值．图 9为有限元值与按照设计规范得到的设计值的比较分析．塔架的有限元值在设计值的包络线范围内，可以说明日本的设计规范是偏安全的．预应力钢筋混凝土塔架沿高度方向未出现拉应力，塔架的最大压应力出现在基底处，未超过35,MPa，满足规范的要求．

3.4 开洞对塔架地震响应分析的影响

在塔架结构的底端往往设置工作用洞口，便于对发电设备等进行定期安全检查．笔者根据文献[10]，设计了塔架的开洞尺寸，如图 10所示．塔架开洞的底端位于基础以上 2.25,m 处，由于塔架底部开洞会对塔架的强度产生不利的影响，采用了贴补强钢板的形式来加强洞口处．

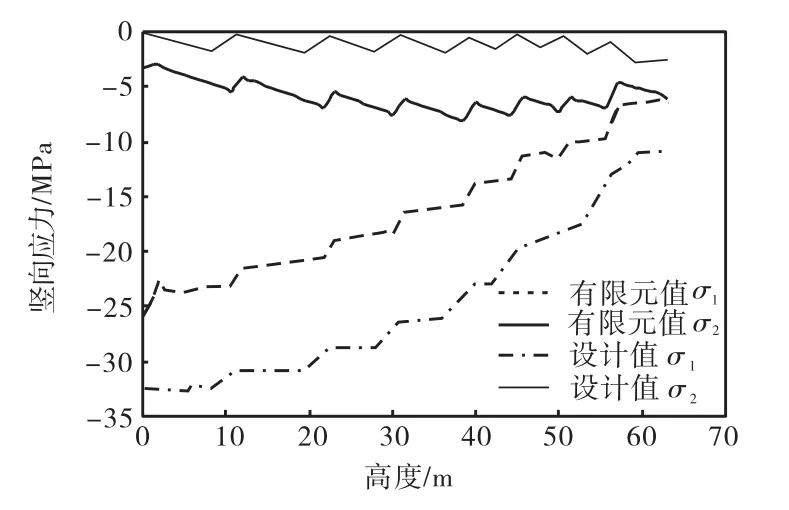
图9 竖向应力有限元值与设计值的比较Fig.9 Comparison between FEM value and design value

图10 塔架开洞的几何尺寸Fig.10 Geometrical size of working hole

图11为时间点10.78,s时(最不利情况下)，工作用洞口设置后，塔架底部的竖向应力分布图和补强钢板的Von miss应力分布图．计算结果表明，整个塔架的应力最大值发生在开洞附近的个别微小区域，外露的预应力钢筋周围产生明显的应力集中现象．开洞后塔架结构的最大竖向应力值为33.2,MPa，补强钢板的 Von Miss应力最大值为 124,MPa，均满足规范的要求．

图 12和图 13分别为开洞对塔顶的位移时程和基底的竖向应力时程的影响图．从图中可以得出，开洞之后对塔架顶端的位移值影响很小，这表明工作用洞口的设置对塔架整体刚度的影响甚微．另外，工作用洞口的设置对未开洞一侧的竖向应力值影响较小，而对开洞一侧的局部竖向应力值影响比较大．在5,s之后，竖向应力值能够稳定的变化，变化的周期与一阶固有周期一致．开洞之后，塔架未开洞侧和开洞侧的竖向应力值围绕某一平均值呈对称变化，未开洞一侧竖向应力值的平均值和幅值有所提高，而开洞一侧竖向应力值的平均值和幅值有所下降．

图11 塔架开洞处周围的应力分布Fig.11 Distribution of stress around the working hole

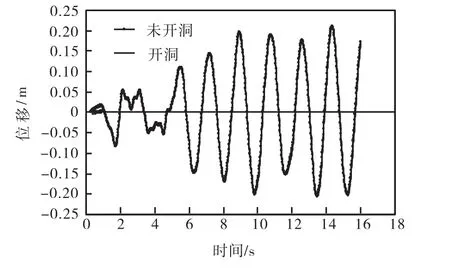
图12 开洞对塔架顶点位移的影响Fig.12 Influence of working hole on the top displacement of the tower

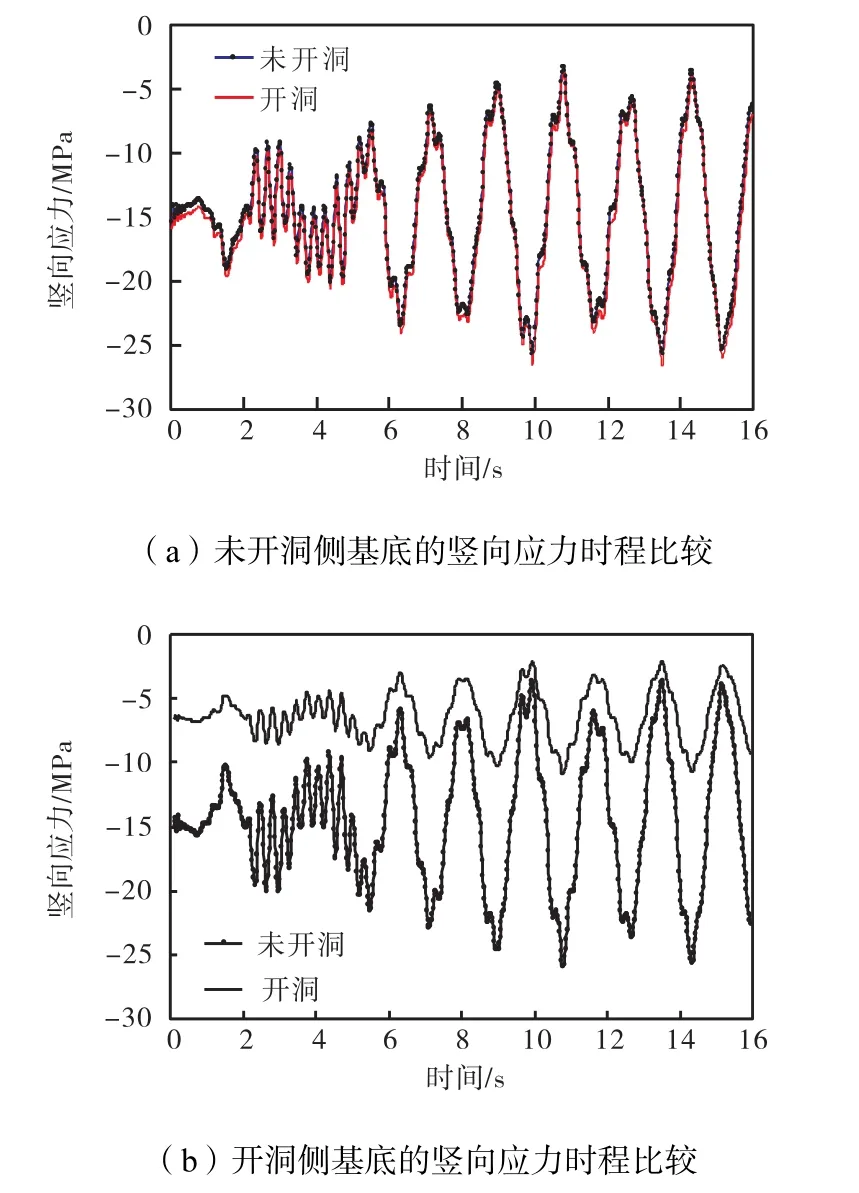
图13 开洞对塔架基底竖向应力的影响Fig.13 Influence of working hole on the foot vertical stress of the tower

3.5 地震波入射角的影响

图14为沿不同方向输入地震波，研究EL Centro波的不同入射角对塔架地震响应的影响．考虑到塔架结构的对称性和地震波输入方向上的相位差，当从0°～360°输入地震波时，可以等同为从0°～180°输入地震波．θ为地震波输入方向与洞口垂直向的夹角，不同方向输入地震波时，即θ=0°、θ=30°、θ=45°、θ=60°、θ=90°、θ=120°、θ=135°、θ=150°和θ=180°．

由图 14可知，当地震波输入方向和洞口垂直向成 0°或者 180°夹角时，地震对塔架结构影响最大．这是因为受开洞的影响，预应力钢筋混凝土塔架结构沿开洞方向上刚度会下降；开洞会使洞口附近产生应力集中；再加上当地震波输入方向和洞口垂直向成0°或者180°夹角时，塔架在沿开洞方向上，其基底处的竖向应力值最大．所以当入射角为 0°或者 180°时，地震波对塔架结构的影响最大．

另外，由图14还可得出，不同入射角地震作用时塔架结构的抗震性能均是安全的．随着θ值变大，开洞侧和未开洞侧的竖向应力值的幅值均呈下降趋势，而平均值保持稳定．将图 13(a)与(b)曲线对比可知，未开洞一侧的竖向应力幅值大于开洞一侧的幅值．

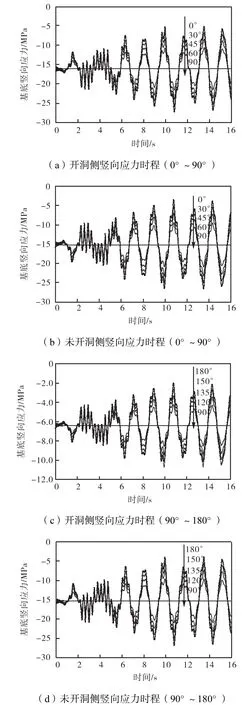
图14 不同地震波入射角时结构的地震响应分析Fig.14 Seismic responses to different-direction earthquake inputs

4 结 论

本文采用数值模拟仿真技术，对预应力钢筋混凝土风力发电塔架进行了模态分析和地震响应分析，讨论了相关参数对地震响应分析的影响．

(1) 塔架的一、二阶固有频率在安全频率范围之内，三阶以后各阶远离标定工作转速，因此可以避免由叶轮脉动激励的共振响应．

(2) 塔架结构竖向应力的有限元分析值，在设计指南得出值的包络线范围内，说明运用日本土木学会的设计指南进行设计是合理的．该设计指南提倡的方法不涉及复杂的有限元分析，具有便于工程人员进行实际设计工作的优点，但其结果有过于安全的倾向．为了达到经济设计的目的，建议在条件允许的情况下采用本文提出的有限元分析方法．其简单流程为对按照规范设计得出的塔架模型进行几何变参数的有限元计算，并对计算结果进行分析，总结规律，进而实现对塔架的优化设计．

(3) 塔架各高度处均未出现拉应力，在基底出现最大压应力；同一塔架位置越高的点，水平位移值越大，竖向压应力值越小，表明塔架截面按照变截面来设计是合理的．

(4) 工作用洞口的设置对塔架整体刚度的影响甚小，但对塔架开洞一侧的局部竖向应力影响比较大，而未开洞侧和开洞侧的竖向应力值仍围绕某一平均值呈对称变化．5,s后竖向应力值能够稳定的变化，变化的周期与一阶固有周期一致．当地震波输入方向和洞口垂直向成 0°入射角时，地震对塔架结构影响最大；不同入射角地震作用时塔架结构的抗震性能均是安全的．

［1］宫靖远. 风电场工程技术手册[M]. 北京：机械工业出版社，2004.

Gong Jingyuan.Technical Handbook of Wind Farm[M].Beijing：China Machine Press，2004(in Chinese).

［2］Singh A N. Concrete construction for wind energy towers[J].The Indian Concrete Journal，2007，81：43-49.

［3］Reinhard Harte，Gideon P A G，Van Zijl. Structural stability of concrete wind turbines and solar chimney towers exposed to dynamic wind action[J].Journal of Wind Engineering and Industrial Aerodynamics，2007，95：1079-1096.

［4］Bazeos N，Hatzigeorgiou G D，Hondros I D，et al. Static，seismic and stability analyses of a prototype wind turbine steel tower[J].Engineering Structures，2002，24：1015-1025.

［5］Lavassas I，Nikolaidis G，Zervas P，et al. Analysis and design of the prototype of a steel 1-MW wind turbine tower[J].Engineering Structures，2003，25：1097-1106.

［6］李长风. 风力发电结构动力反应的一体化有限元模型分析[J]. 特种结构，2008，25(2)：17-19.

Li Changfeng. Integrated finite element model analysis of seismic response for wind turbine structure[J].Special Structures，2008，25(2)：17-19(in Chinese).

［7］Witcher D. Seismic analysis of wind turbines in the time domain[J].Wind Energy，2005，8：81-91.

［8］谢 峰，赵吉文，沈维蕾，等. 600 kW 风力机塔架结构的仿真设计[J]. 系统仿真学报，2004，16(1)：70-72，90.

Xie Feng，Zhao Jiwen，Shen Weilei，et al. Simulating design of the tower structure for 600 kW-wind turbine[J].Journal of System Simulation，2004，16(1)：70-72，90(in Chinese).

［9］沈聚敏. 抗震工程学[M]. 北京：中国建筑工业出版社，2004.

Shen Jumin.Aseismic Engineering[M]. Beijing：China Architectural Industry Press，2004(in Chinese).

［10］Japan Society of Civil Engineers.Guidelines for Design of Wind Turbine Support Structures and Foundations[S].Tokyo，2007.