光滑壁面明渠水流的三维格子玻耳兹曼模拟

丁 磊，张庆河

(天津大学建筑工程学院港口与海洋工程教育部重点实验室，天津 300072)

明渠流是自然界和工程实践中常见的一种水流运动，泥沙运动以及河床演变等问题都与之密切相关．国内外学者主要采用实验、理论分析和数值模拟的方法进行明渠均匀流的研究．在实验研究方面，Nezu等[1]采用二维激光多普勒流速仪(LDA)研究了水槽中光滑壁面均匀紊流，认为近底附近的时均流速分布可以用对数律来描述，同时还存在着分区结构，后续的相关实验[2-3]也证实了这一观点．实验研究为认识明渠均匀流的水流特性和紊动结构奠定了基础．在理论分析方面，研究者主要从恒定明渠紊流的雷诺方程出发推导光滑壁面时均流速、切应力以及雷诺应力分布[4-6]．在明渠紊流的数值模拟方面，各种紊流模型、大涡模拟(LES)以及直接数值模拟(DNS)都得到了应用[7-9]．数值模拟结果提供了比实验更为详细的明渠水流紊动特性和整体流场信息，为进一步研究明渠流中的泥沙运动规律打下了基础．但由于问题的复杂性，在水流与泥沙颗粒耦合模拟方面还有很多问题有待深入研究．为此，寻找新型数值模拟方法研究明渠水流，特别是明渠水流作用下的泥沙运动仍是值得探索的工作．

近年来，格子玻耳兹曼(lattice Boltzmann，LB)方法在许多学科领域得到了广泛应用．LB方法具有易于处理固体边界、易于并行计算等特点，较传统的数值计算方法更容易处理动边界且更容易对流体动力作用下的大规模颗粒运动进行全尺度直接模拟[10-13]．因此，LB方法研究明渠流中的泥沙运动具有较大的优势．目前，LB方法在明渠水流中的应用主要集中于二维模型[14-16]，张金凤等[17]、Fernandino 等[18]采用三维LB结合大涡模拟(LES)对光滑明渠流进行了模拟，但所得到的紊流时均流速分布与解析解或实验值还有一定差距．由于 LES对紊流的模拟存在一定程度的简化，特别是文献中采用的 LES主要是传统的Smagorinsky模式[17-18]，而相关研究表明该模式对壁面附近紊流的描述存在缺陷[19]．鉴于此，笔者进一步采用三维 LB方法对光滑壁面明渠紊流进行直接数值模拟(DNS)，并与解析解和实验结果进行比较，以便为应用 LB方法研究明渠流中泥沙运动机理奠定基础．

1 数值方法

1.1 三维LB方法

与传统的计算流体力学方法直接离散求解Navier-Stokes(N-S)方程不同，LB方法是在介观层面上构建简化的离散速度动力学模型，即格子模型，通过控制格子模型中虚拟粒子的密度分布函数演化过程使计算域中流体在宏观层面上表现出 N-S方程控制的性质．演化过程的控制方程即为 LB方程[20]，如式(1)所示．

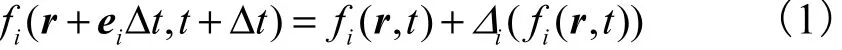
式中：r为位置矢量；ei为格子模型中离散速度矢量；i为离散速度方向；t为时间变量；tΔ为时间步长；if为密度分布函数；iΔ为碰撞算子．

密度分布函数与宏观流体变量(密度ρ和动量密度ρu)的关系如式(2)和式(3)所示．

在本文的三维计算中，选取了D3Q19格子模型，即离散速度的个数为 19，离散速度矢量的具体分布形式如式(4)所示．

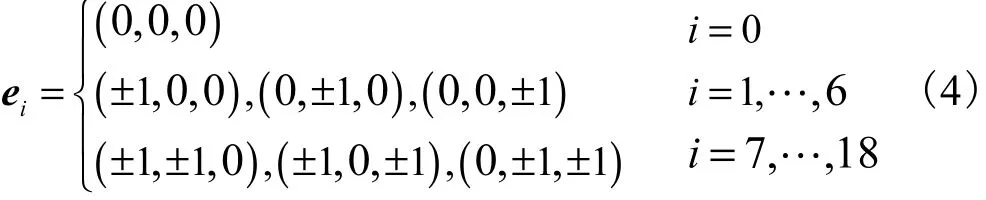
1.2 LB模拟流动的驱动方式

LB中常用的产生流体运动的驱动方式主要有3种[21]：①将流体所受体积力作为外力项加入 LB方程来实现；②作用压力梯度，而对于不可压缩流体则往往将压力梯度转化成体积力作为驱动力；③在入口边界给定速度分布．张金凤等[17]采用体积力的方式实现明渠水流的驱动，但给出的体积力的计算方法主要适用于层流情况，在明渠紊流中使用则会由于雷诺应力的影响带来一定的偏差．Fernandino等[18]也将压力梯度转化成体积力来进行计算，所得到的时均流速分布与实验值同样存在差距．为消除压力作为体积力驱动时可能形成的误差，这里笔者采用入口速度驱动的方式．

1.3 边界条件

图 1给出了模拟时的三维坐标、水流流动方向以及各边界的位置．计算区域的入口设置速度边界条件[22]，侧边界和出口处施加周期性边界条件，底面采用无滑移边界条件，自由表面则采用自由滑移边界条件[21]进行近似处理．由于这里主要研究明渠近底水动力特性，选取自由滑移边界条件是合适的．

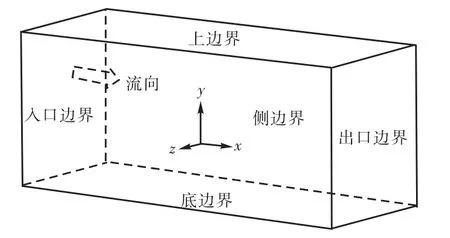
图1 计算区域与边界示意Fig.1 Sketch of computational domain and boundary

1.4 紊流的描述

明渠底面的存在使得水流紊动变得更加复杂．底面附近紊动的合理描述对认识明渠流近底水动力特性以及揭示泥沙颗粒运动机理具有重要意义．在数值模拟中，由于DNS无需对流动做任何简化或近似，可以比较完整准确地反映紊动特性，已经越来越多地应用于紊流特别是壁面紊流的研究中[23-24]．因此，本文采用DNS方法来模拟近底水流紊动．

2 明渠均匀流模拟

2.1 模型验证

为验证建立的模型，首先计算明渠层流情况．明渠层流流速沿水深的分布如式(5)所示，满足抛物线关系[25]．

式中：u( y)为距底面距离为y处的流速值；umax为流速分布的最大值；h为明渠水深．这里取h＝1.0×10-2,m，umax＝7.2×10-2,m/s，以断面平均流速 Um定义雷诺数Re＝Umh/ν＝480，v为水的运动黏滞系数．计算区域沿流向、水深及宽度方向分别取为10×10-2、1×10-2和2×10-2,m．需要说明的是，由于流动处于层流状态时，各层流体之间相互影响较小，因此为减少计算时间，在水深方向上只选取了底面以上1×10-2,m的区域．采用立方体网格离散计算域，沿流向、水深及宽度方向网格数分别为1,000、100、200，网格大小为Δx=Δy=Δz = 1× 1 0-4m．计算中将式(5)作为入口速度边界条件．

明渠层流中各层切应力τ,如式(6)所示，容易看出，切应力沿水深呈线性分布．

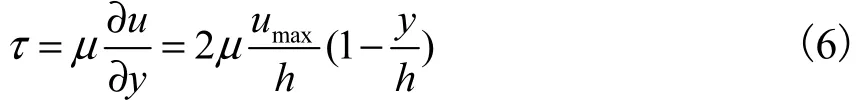
式中μ为水的动力黏滞系数．

图2给出了计算区域中间断面流速分布与式(5)的比较结果，图3给出了切应力分布与式(6)的比较结果．由图2和图3可知，流速分布与切应力分布的模拟结果与解析解有很好的一致性，这说明所建立的 LB模型可以应用于低雷诺数时明渠均匀层流的模拟．

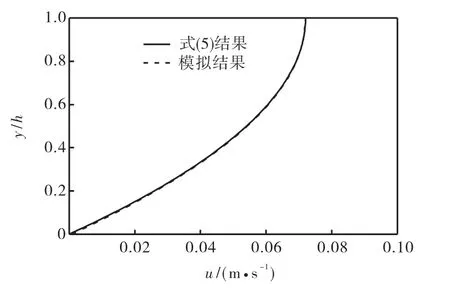
图2 明渠层流流速分布Fig.2 Velocity profile of laminar open channel flow

图3 明渠层流切应力分布Fig.3 Shear stress profile of laminar open channel flow

2.2 光滑壁面明渠紊流近底水流模拟

2.2.1 算例设置

进一步将 LB模型应用于光滑壁面明渠紊流近底运动的模拟，为便于与实验结果比较，计算时选取Nezu等[1]的实验条件，具体参数见表1．

表1 实验参数Tab.1 Experimental parameters

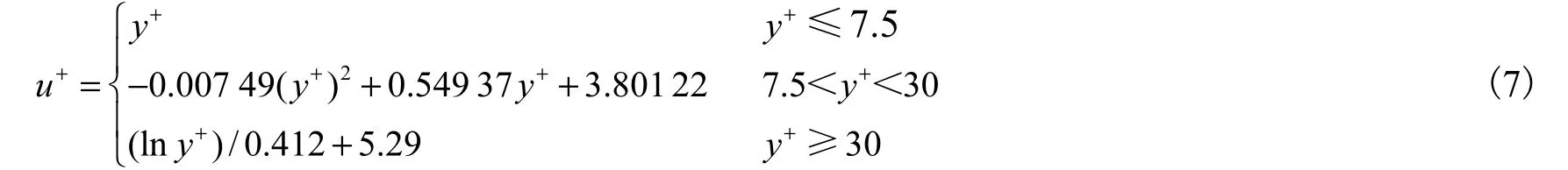
根据以往实验研究和理论分析的成果[1-2]，光滑壁面明渠紊流近底存在着时均流速分布的分区结构，沿水深方向由下至上依次为黏性底层、过渡层和对数层．黏性底层内的流速呈线性分布，对数层内的流速符合对数律，过渡层由于受边界条件等因素影响较大，尚没有统一的流速分布表达式．在设置入口速度边界条件时考虑了分区结构，其中黏性底层和对数层中的流速分布表达式均引自文献[1]，这里对过渡层的流速分布做了简化处理，在已知黏性底层和对数层流速后利用二次曲线拟合连接，具体形式见式(7)．

式中：u+=u/ u*1；y+= u*1y/ν．为了加快紊动的发展，入口边界条件在式(7)的基础上叠加了随机小幅扰动．计算区域选择在实验渠道的中心断面附近，沿流向、水深方向、宽度方向分别取10×10-2,m、3×10-2,m、2×10-2,m．需要指出的是，由于主要研究近底水动力条件，考虑到DNS的计算较为耗时，在保证计算精度和计算效率的情况下，本文在水深方向减小了计算区域，只选取了底面以上3×10-2,m 的区域，此时计算域的上边界仍处于对数层，受自由表面影响很小．计算域采用立方体网格离散，沿流向、水深和宽度方向的网格数分别为 1,000、300和 200，网格大小为Δx = Δy = Δz = 1× 1 0-4m，换算至量纲1的壁面单位表示为 Δ x+=Δ y+=Δ z+= u*1Δ x /ν= 0 .431，网格精度满足DNS的计算要求[26]．

2.2.2 流速分布

图4(a)显示了计算区域中部第60,000时间步的瞬时流速垂向剖面，图 4(b)则给出了时均流速垂向剖面(取最后 40,000时间步进行时间平均)与式(7)和实验结果的比较．从瞬时流速分布看，流速剖面较好地反映了垂向分区特性．由图 4(b)可知，计算值与理论分析及实验结果均符合较好，说明式(7)中采用二次曲线拟合过渡层的流速分布是合理的．

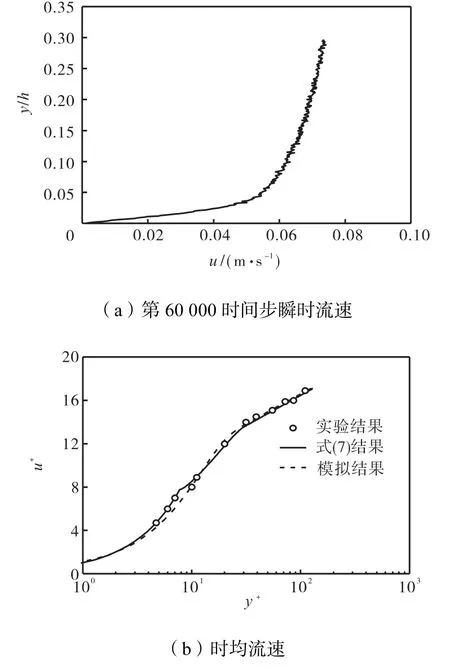
图4 光滑壁面明渠紊流流速分布Fig.4 Velocity distribution of smooth turbulent open channel flow

2.2.3 切应力

总的时均切应力由时均黏性应力和雷诺应力两部分构成．图5给出了明渠中部沿流向剖面的无量纲时均黏性应力τ1*= (μ∂ u / ∂ y ) /的等值线分布．由图5可知，时均黏性应力在壁面附近最大，在距壁面一定位置后迅速减小，这与已有的认识是一致的[1,27]．

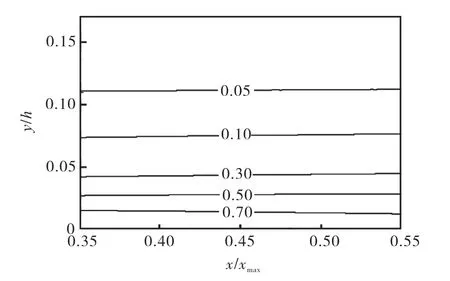
图5 时均黏性应力等值线分布Fig.5 Contours of time-averaged viscous stress

无量纲雷诺应力可用τ*=-'/ u2表示，图 6给出了τ2*沿水深分布的模拟结果与实验结果的比较情况．两者最大相对误差的绝对值为 6.8%，说明计算结果与实验结果符合较好．同时图 6还反映了雷诺应力沿水深方向除壁面附近外基本为线性分布，这也与实验和理论分析结果相符[1,27]．

底面时均切应力是流动阻力规律研究的关键，特别是由其定义的摩阻流速对流速分布和紊动特性有重要影响．利用计算结果并根据董曾南等[2]给出的方法计算了底面时均切应力，并将其换算成摩阻流速(0.389×10-2,m/s)，与实验得到的摩阻流速(0.431×10-2m/s)相比，相对误差为 9.74%，说明计算结果可以较好地反映底面时均切应力．由于计算所采用的实验条件中明渠水流的宽深比为 5.9，中心区域受侧壁影响较小，底面时均切应力沿宽度方向即横向分布应较为均匀，图7给出的中间断面底面时均切应力τ0的横向分布说明了这一点．

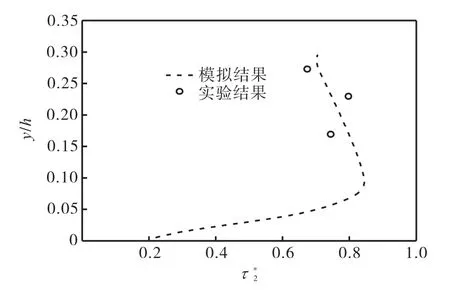
图6 雷诺应力分布Fig.6 Reynolds stress distribution

图7 底面时均切应力横向分布模拟结果Fig.7 Lateral distribution of bottom shear stress

3 结 语

应用三维 LB方法对明渠均匀流进行了模拟，为了避免以往 LB计算中压力作为体积力驱动水流可能形成的误差，采用了入口速度驱动方式．将该方式应用于明渠层流模拟时，流速和切应力沿水深分布与解析解吻合很好．对于光滑壁面明渠紊流，采用 DNS方式模拟水体紊动，并重点对近底水动力特性进行了模拟研究．模拟得到的时均流速分布与考虑水流垂向分区结构的流速分布理论解和实验结果均符合较好．另外，雷诺应力的垂向剖面与实验结果有较好的一致性，从底面时均切应力的横向分布结果也可以看出，建立的模型可以较好地描述近底紊动特性和阻力规律．

从有限的算例结果看，采用的设置入口速度边界条件并结合直接数值模拟的 LB方法，可较准确地反映光滑明渠均匀层流与紊流的近底水动力特性．在此基础上，研究不同雷诺数下光滑明渠近底紊流的水动力特性，并进一步研究粗糙壁面明渠水流的近底水动力特性，从微观角度探索泥沙颗粒运动机理，是下一步需要深入的工作．

［1］Nezu I，Rodi W. Open-channel flow measurements with a laser Doppler anemometer[J].Journal of Hydraulic Engineering，1986，112(5)：335-355.

［2］董曾南，丁 元. 光滑壁面明渠均匀紊流水力特性[J].中国科学A辑，1989(11)：1208-1218.

Dong Zengnan，Ding Yuan. Turbulence characteristics of uniform flow in a smooth open channel[J].Science in China，Ser A，1989(11)：1208-1218(in Chinese).

［3］刘春晶，李丹勋，王兴奎. 明渠均匀流的摩阻流速及流速分布[J]. 水利学报，2005，36(8)：950-955.

Liu Chunjing，Li Danxun，Wang Xingkui. Experimental study on friction velocity and velocity profile of open channel flow[J].Journal of Hydraulic Engineering，2005，36(8)：950-955(in Chinese).

［4］Yang S-Q，McCorquodale J A. Determination of boundary shear stress and Reynolds shear stress in smooth rectangular channel flows[J].Journal of Hydraulic Engineering，2004，130(5)：458-462.

［5］Guo J，Julien P Y. Shear stress in smooth rectangular open-channel flows[J].Journal of Hydraulic Engineering，2005，131(1)：30-37.

［6］刘亚坤，倪汉根. 水力光滑明渠流流速分布的新公式[J]. 水利学报，2007，38(11)：1336-1340.

Liu Yakun，Ni Hangen. New formula for velocity profile of turbulent flow in open channel with smooth wall[J].Journal of Hydraulic Engineering，2007，38(11)：1336-1340(in Chinese).

［7］Kang H，Choi S-U. Reynolds stress modelling of rectangular open-channel flow[J].International Journal for Numerical Methods in Fluids，2006，51(11)：1319-1334.

［8］Hinterberger C，Fröhlich J，Rodi W. 2D and 3D turbulent fluctuations in open channel flow withReτ＝590 studied by large eddy simulation[J].Flow，Turbulence and Combustion，2008，80(2)：225-253.

［9］Honda I，Kanagawa N，Kawashima Y. Direct numerical simulation of open channel flow with buoyancy[J].Developments in Chemical Engineering and Mineral Processing，2003，11(5/6)：465-479.

［10］Ladd A J C，Verberg R. Lattice-Boltzmann simulations of particle-fluid suspensions[J].Journal of Statistical Physics，2001，104(5/6)：1191-1251.

［11］吴锤结，周菊光. 悬浮颗粒运动的格子Boltzmann数值模拟[J]. 力学学报，2004，36(2)：151-162.

Wu Chuijie，Zhou Juguang. Numerical simulation of suspension motion of irregular shaped particles via the lattice Boltzmann method[J].Acta Mechanica Sinica，2004，36(2)：151-162(in Chinese).

［12］Stratford K，Pagonabarraga I. Parallel simulation of particle suspensions with the lattice Boltzmann method[J].Computers and Mathematics with Applications，2008，55(7)：1585-1593.

［13］Hölzer A，Sommerfeld M. Lattice Boltzmann simulations to determine drag，lift and torque acting on non-spherical particles[J].Computers and Fluids，2009，38(3)：572-589.

［14］程永光，索丽生. 二维明渠非恒定流的格子 Boltzmann模拟[J]. 水科学进展，2003，14(1)：9-14.

Cheng Yongguang，Suo Lisheng. 2-D open channel flow simulations by the lattice Boltzmann model[J].Advances in Water Science，2003，14(1)：9-14(in Chinese).

［15］Li Y，Huang P. A coupled lattice Boltzmann model for the shallow water-contamination system[J].International Journal for Numerical Methods in Fluids，2008，59(2)：195-213.

［16］Liu H，Zhou J G，Burrows R. Numerical modeling of turbulent compound channel flow using the lattice Boltzmann method[J].International Journal for Numerical Methods in Fluids，2009，59(7)：753-765.

［17］张金凤，张庆河. 明渠流中分形絮团破裂的格子Boltzmann方法模拟[J]. 天津大学学报，2009，42(1)：17-23.

Zhang Jinfeng，Zhang Qinghe. Lattice Boltzmann simulation of the breakup process of fractal flocs in openchannel flows[J].Journal of Tianjin University，2009，42(1)：17-23(in Chinese).

［18］Fernandino M，Beronov K，Ytrehus T. Large eddy simulation of turbulent open duct flow using a lattice Boltzmann approach[J].Mathematics and Computers in Simulation，2009，79(5)：1520-1526.

［19］Sagaut P.Large Eddy Simulation for Incompressible Flows：An Introduction[M]. 3rd ed. Berlin：Springer，2006.

［20］Chen S，Doolen G D. Lattice Boltzmann method for fluid flows[J].Annual Review of Fluid Mechanics，1998，30(1)：329-364.

［21］Dupuis A. From a Lattice Boltzmann Model to a Parallel and Reusable Implementation of a Virtual River[D]. Geneva：University of Geneva，2002.

［22］He X Y，Zou Q S，Luo L S，et al. Analytic solutions of simple flows and analysis of nonslip boundary conditions for the lattice Boltzmann BGK model[J].Journal of Statistical Physics，1997，87(1/2)：115-136.

［23］Lammers P，Beronov K N，Volkert R，et al. Lattice BGK direct numerical simulation of fully developed turbulence in incompressible plane channel flow[J].Computers and Fluids，2006，35(10)：1137-1153.

［24］Wu X，Moin P. Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer[J].Journal of Fluid Mechanics，2009，630：5-41.

［25］格拉夫，阿廷拉卡. 河川水力学[M]. 赵文谦，万兆惠，译. 成都：成都科技大学出版社，1997.

Graf W H，Altinakar M S.River Hydraulics[M]. Zhao Wenqian，Wan Zhaohui，Trans. Chengdu：Chengdu Science and Technology University Press，1997(in Chinese).

［26］Singh K M，Sandham N D，Williams J J R. Numerical simulation of flow over a rough bed[J].Journal of Hydraulic Engineering，2007，133(4)：386-398.

［27］章梓雄，董曾南. 粘性流体力学[M]. 北京：清华大学出版社，1998.

Chwang A T，Dong Zengnan.Viscous Fluid Mechanics[M]. Beijing：Tsinghua University Press，1998(in Chinese).