基于IOWA算子的赤潮LMBP神经网络组合预测模型

张承慧，钱振松，孙文星，姬 鹏，胡 婧

(1. 山东大学控制科学与工程学院，济南 250061；2. 山东师范大学管理与经济学院，济南 250014；3. 中国科学院地理科学与资源研究所，北京 100101)

赤潮预测是当今国内外赤潮研究领域中一个重要研究方向．近年来赤潮频繁爆发，破坏了正常的海洋生态系统平衡，严重危害了海洋渔业资源和海产养殖业，并造成了巨大的经济损失，因此，开展赤潮预测研究有重要意义和实际应用价值．目前，已有多位学者利用神经网络算法构建了不同的赤潮预测模型[1-5]，取得了一定研究成果．其中Joseph等建立了基于BP神经网络的赤潮预测预警模型[3]；马玉梅等[4]采用了附加动量法的 BP网络算法对赤潮进行预测预警；王洪礼等[5]建立了基于模糊神经网络赤潮预测模型．但是现有基于神经网络的赤潮预测模型大多采用标准 BP学习算法，并且多为单项预测模型，存在预测精度低、稳定性差和信息利用率低的问题．

针对目前赤潮神经网络预测模型的不足，笔者提出了一种赤潮组合预测模型，该模型基于诱导有序加权平均(induced ordered weighted average，IOWA)算子与Levenberg-Marquardt back propagation(LMBP)神经网络算法．首先针对赤潮频发的特点选择输入变量，进而通过多组对比实验确定最优LMBP网络结构，然后引入IOWA算子，将单项LMBP神经网络预测的输出结果按照拟合精度的高低顺序赋权，建立赤潮组合预测模型，并给出确定最优权值的计算方法．

1 LMBP神经网络

人工神经网络理论在处理非线性模式识别方面已表现出了很好的特性，BP网络是目前应用最为广泛的一种前馈神经网络模型，具有较强的自学习能力和处理非线性问题的能力．但是标准BP算法的收敛速度慢，且在训练过程中易陷入局部极小点，从而导致模型精度不高[6]．1994年，Hagan等[7]首次提出使用L-M数值优化算法对BP网络进行改进，在一定程度上克服了标准BP算法的上述缺点．

图1所示为S1维输入、S3维输出的BP网络，上一层的输出为下一层的输入，网络结构为 S1-S2-S3，字母上标表示网络层序号．

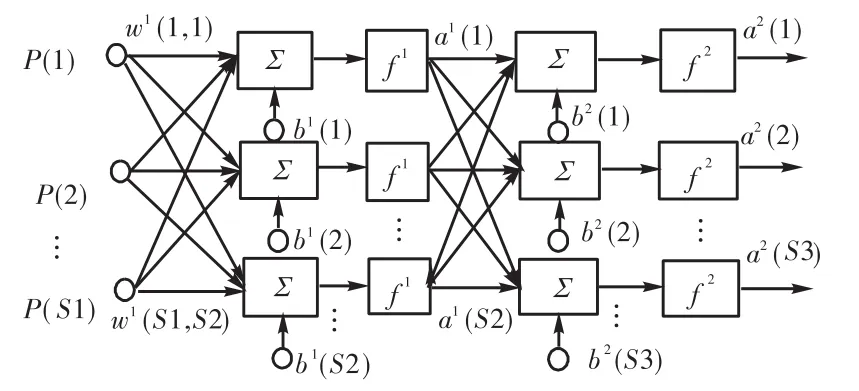
图1 前向神经网络结构Fig.1 Multi-layer feed-forward neural network structure

对于一个 M 层的神经网络，其前向传播过程可以表示为

式中：k＝0，1，…，M-1；n 为 k+1 层输入；a 为该层的输出；f为传递函数；w为两层神经元之间的权值；b为阈值．

2 IOWA算子

针对常用单项预测模型信息源利用不够广泛的问题，Bates等[8]于 1969年首次系统阐述了组合预测的概念，并证明了2种或2种以上无偏的单项预测模型可以组合出优于每个单项模型的预测结果，从而有效提高了预测精度，改善了预测结果．因此，组合预测受到国内外预测学者的重视．然而，尽管传统组合预测模型能够在一定程度上综合各个单项模型的有效信息，优化单项预测结果，但是其问题在于：同一单项模型在某一样本区间上各个时刻的加权平均系数是相同的．针对上述问题，Yager[9-10]于 1999年提出了诱导有序加权平均(IOWA)算子，依据各单项预测模型在不同时刻预测精度的高低来赋权，很好地克服了此问题．

定义表明 IOWA算子是对诱导值 v1, v2, v3,… ,vm按从大到小顺序排列后所对应的 a1, a2, a3,… ,am中的数进行有序加权平均，wi与数 ai的大小和位置无关，而与其诱导值 vi所在的位置有关．

3 赤潮组合预测模型实例分析

3.1 确定以各理化因子为输入的单入单出最优LMBP网络模型

3.1.1 数据样本选取与数据规范化预处理

2007年 7—8月间，烟台四十里湾海域爆发了赤潮，持续时间达 1个月．期间国家海洋局北海分局烟台海洋环境监测中心站对该海域进行了有效监测．本文选取47组完整数据，并将前37组样本用作网络训练样本，后10组样本用作网络测试样本，部分监测数据如表 1所示．监测的 10种理化因子为：水温、透明度、pH值、盐度、化学耗氧量(COD)、溶解氧(DO)、磷酸盐、总氮、叶绿素a和浮游植物密度．

为了满足LMBP网络输入输出对数据的要求，同时避免测试结果出现较大误差，在进行训练网络及测试前，必须要对输入输出数据进行统一的规范化处理，按式(3)进行规范化处理，使其在 0.1～1.0范围内．

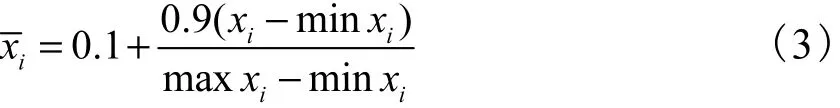
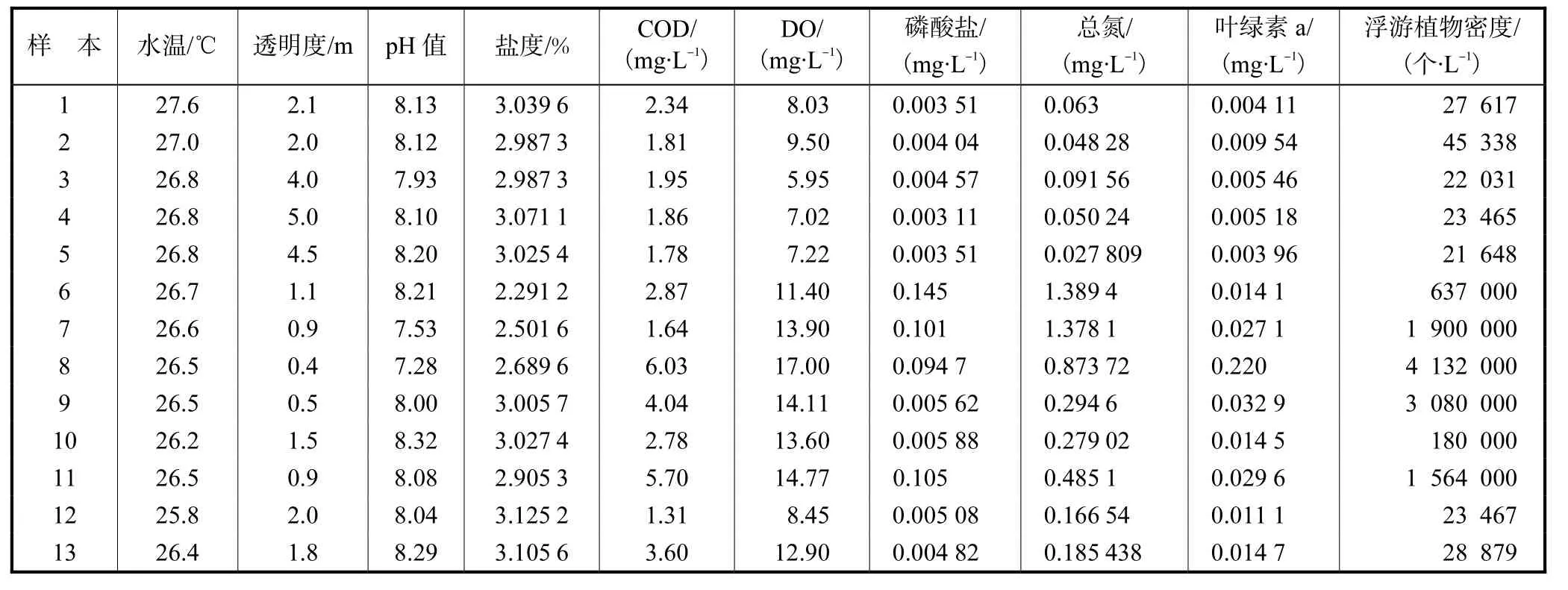
表1 北海分局四十里湾部分监测数据Tab.1 Partial monitoring data of Yantai Sishili Bay collected by North China Sea branch, SOA

3.1.2 选取输入变量、激励函数并确定最优 LMBP网络结构

到目前为止，在世界范围内赤潮发生机制方面的研究尚未取得重要突破，因此对烟台四十里湾海域进行赤潮预测的建模过程中，为了能得到更加准确的预测结果，选择模型的输入亦是一个难点．

由于理化因子的测量误差不可避免，输入越多，引入的干扰就可能越多，特别是无关因子的引入，不仅会导致模型的精度降低，更会延长网络的训练时间，因此本文选取单个理化因子作为网络输入，即分别以水温、透明度、pH值、盐度、化学耗氧量(COD)、溶解氧(DO)、磷酸盐、总氮和叶绿素a作为LMBP网络的输入．

不同的激励函数对网络的性能如收敛速度等也有重要影响，但是目前并没有完善的理论来确定网络激励函数，故本文中采用实验方法，以10次网络误差(mean squared error，MSE)的平均值最低为目标，最终选取 tansig、purelin分别作为隐含层、输出层的激励函数．具体结果如表2所示．

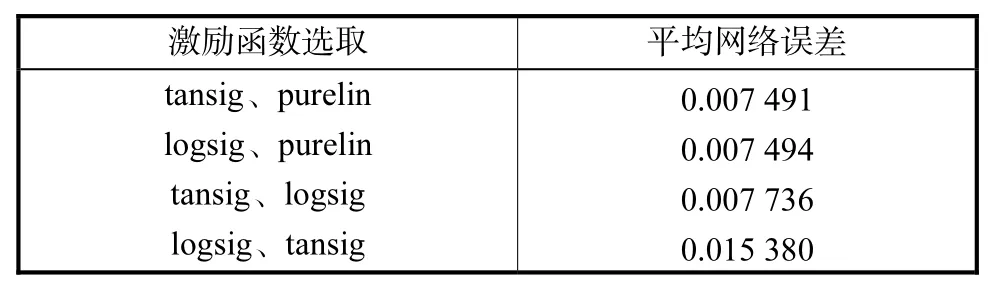
表2 不同隐含层、输出层激励函数选取的实验结果Tab.2 Average MSE of different hidden and output activate functions

由于单隐层的 BP网络即可以逼近任意的非线性映射，故在本文实验中采用了单隐层的网络结构，并以均方误差MSE最小为原则，通过多次比对实验，确定最优隐含层神经元的个数．

基于以上方法，采用 MATLAB,7编程，以批处理方式进行网络训练，网络误差指标设定为 0.005，最大训练次数设定为 200次，分别以 tansig、purelin作为隐含层、输出层的激励函数，最终确定了 9组分别以单个理化因子为输入的、浮游植物密度为输出的、单隐层的单项LMBP神经网络，具体见表3．

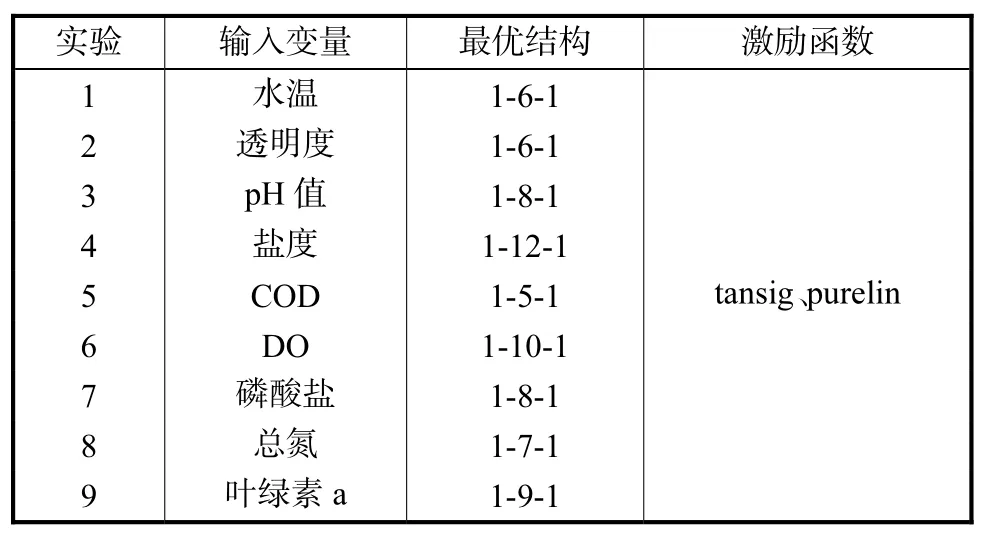
表3 输入变量组合及最优LMBP网络结构Tab.3 Groups of input variables and the optimal structure Tab.3 of LMBP neural networks

3.2 基于 IOWA算子的单入单出 LMBP组合预测模型

本文提出的组合预测模型，首先构造了9个单入单出LMBP网络预测模型，然后利用IOWA算子将9个单项网络输出的浮游植物密度预测值进行集结，最后以均方误差 MSE和平均相对误差(mean relative percentage error，MRPE)作为评价指标，评价该组合预测模型的预测效果，并通过拟合对比图进行直观显示．结构如图2所示．

下面将详细论述如何利用 IOWA算子进行信息集结，共需经过诱导因子计算、误差信息方阵计算、最优化模型建立和最优权系数计算4个步骤．

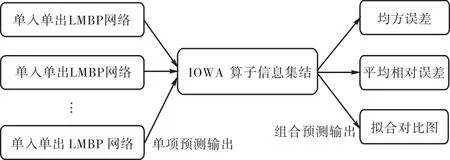
图2 IOWA算子组合预测模型结构Fig.2 Structure of combination forecast model based on Fig.2 IOWA operator

3.2.1 计算诱导因子

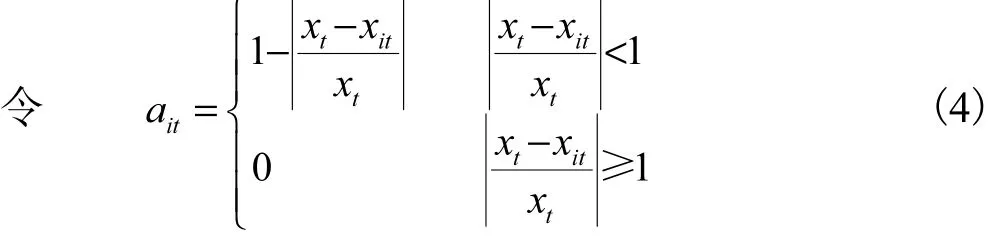
设某参数序列的测量值为 { xt, t = 1 ,2,… ,N }，设有m种可行的单项预测方法对其进行预测，其中第 i种预测方法第 t时刻的预测值为 xit，并有 i = 1,2,… ,m,t = 1,2,… ,N.则 ait表示第i个预测模型第t时刻的预测精度，显然ait∈ [ 0 , 1].把预测精度 ait看成预测值 xit的诱导值，这样第 t时刻 m种单项预测模型预测精度和其对应的预测值就构成了m个二维数组，即

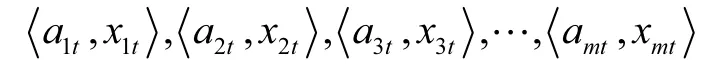
设W=(w , w , w , … ,w )T为单项预测模型在组合

1 2 3m预测中的有序加权平均向量，将 m个单项预测模型第t时刻预测精度序列 a1t, a2t, a3t, … ,amt按从大到小的顺序排列，设 a - index(it)是第 t时刻第 i个大的预测精度的下标，根据IOWA算子定义，则式(5)称为由预测精度序列 a1t, a2t, a3t, … ,amt产生的诱导有序加权平均组合预测值[11]．

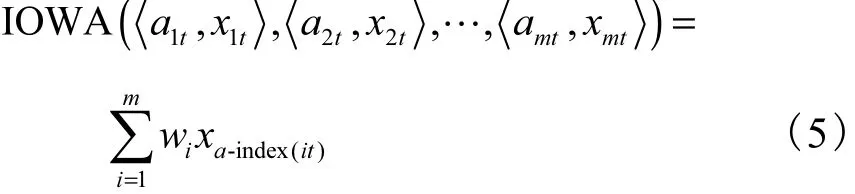
取表 3所得最优 LMBP网络 10次实验的平均输出值，作为组合预测模型的输入，根据式(4)计算诱导因子，具体如表4所示．

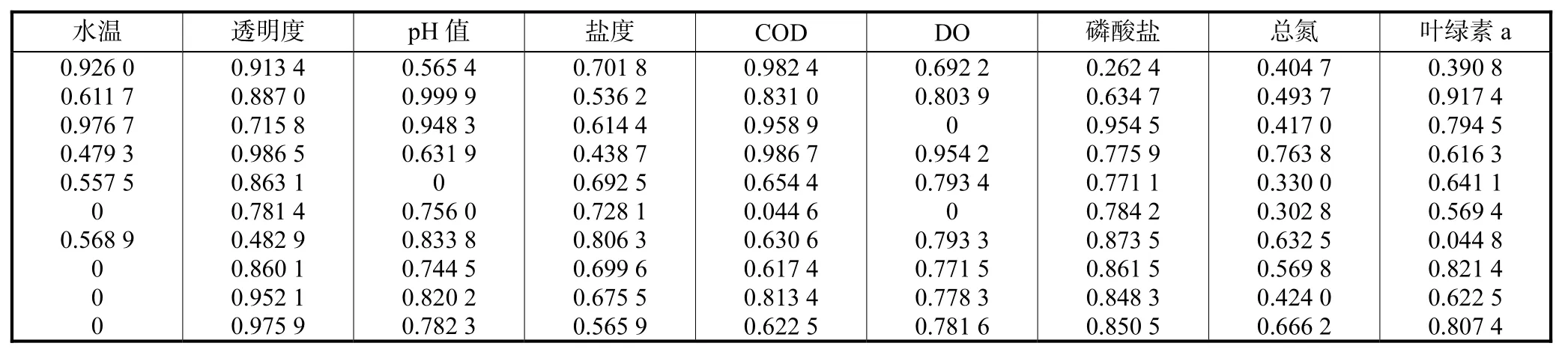
表4 诱导因子Tab.4 Induced index of 10 different LMBP neural networks

3.2.2 计算误差信息方阵

令 ea-index(it)= xt-xa-index(it),于是N个模型总的预测

误差平方和F为

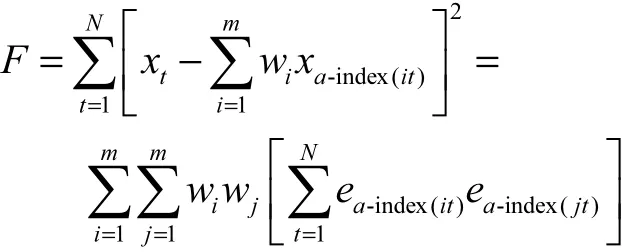
因此，新的诱导有序加权平均组合预测模型可表示为

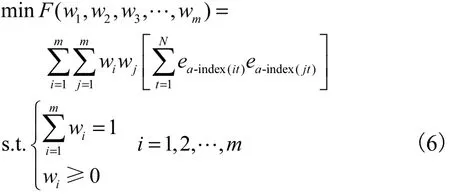
3.2.3 计算最优权系数

根据式(7)，得出最优化模型，即

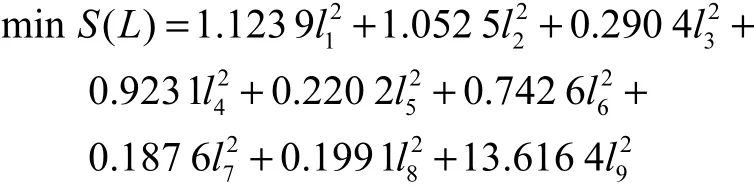
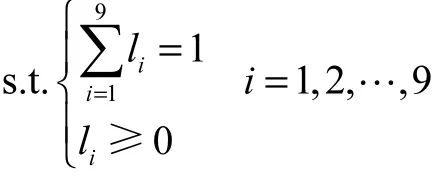
计算得出组合预测模型最优权系数为 l1=0，l2=0，l3=0，l4=0，l5=0，l6=0，l7=0.788 9，l8=0.211 1，l9=0.

组合预测模型的IOWA最优权系数表明，输入分别为磷酸盐、总氮的2个单输入单输出LMBP网络预测模型的权系数为非零，其他7个单输入单输出LMBP网络预测模型的权系数为零．其意思是指组合预测值是分别为磷酸盐、总氮的2个单输入单输出LMBP网络预测模型预测值的最优线性加权值，其他的单项预测模型预测值为冗余信息，即烟台四十里湾海域赤潮的频繁爆发与磷酸盐和总氮的浓度密切相关，而与其他理化因子的浓度相关不大．显然，即使传统的模型与本文提出的IOWA算子最优组合预测模型获得相同的预测结果，其实际含义也是不同的．

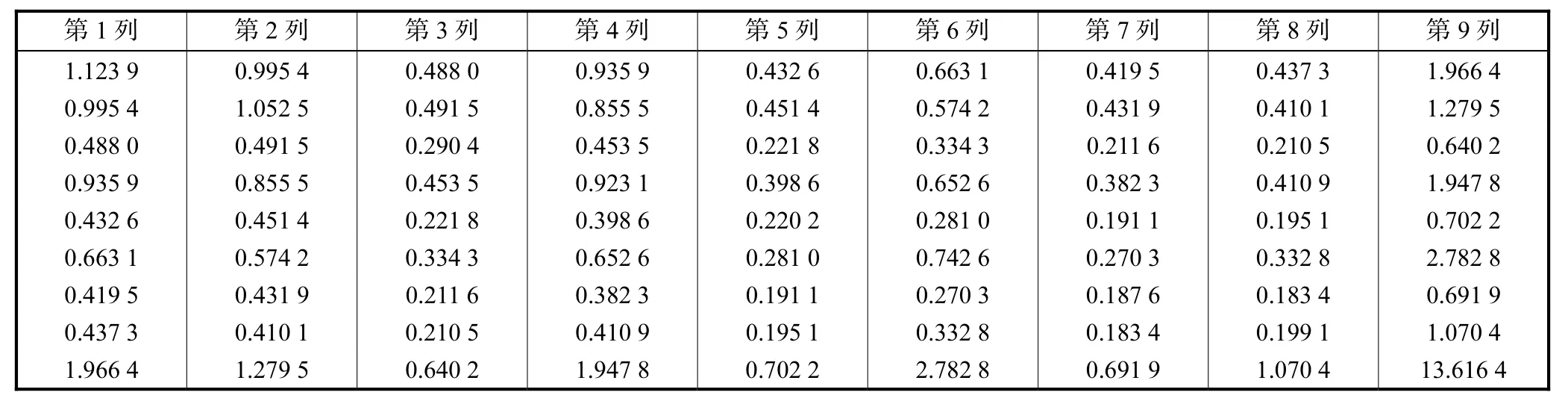
表5 误差信息方阵ETab.5 Square matrix of error E

3.3 预测性能评价

为了验证组合预测模型(记为 IOWA 模型)的有效性，本文根据相同的方法构造了 3个 LMBP网络预测模型：输入为磷酸盐、网络结构为 1-8-1的单输入单输出 LMBP网络预测模型(记为 L-LMBP模型)；输入为总氮、网络结构为 1-7-1的单输入单输出LMBP网络预测模型(记为 D-LMBP模型)；输入为磷酸盐和总氮、网络结构为 2-6-1的双输入单输出LMBP网络预测模型(记为LD-LMBP模型)．选取6组测试样本进行测试，采用MATLAB 7编程，以批处理方式进行网络训练，网络误差指标设定为 0.005，最大训练次数设定为 200次，分别以 tansig、purelin作为隐含层、输出层的激励函数，以 MRPE和 MSE作为评价指标对 4个模型预测效果进行评价．最终的实验结果如表6所示．

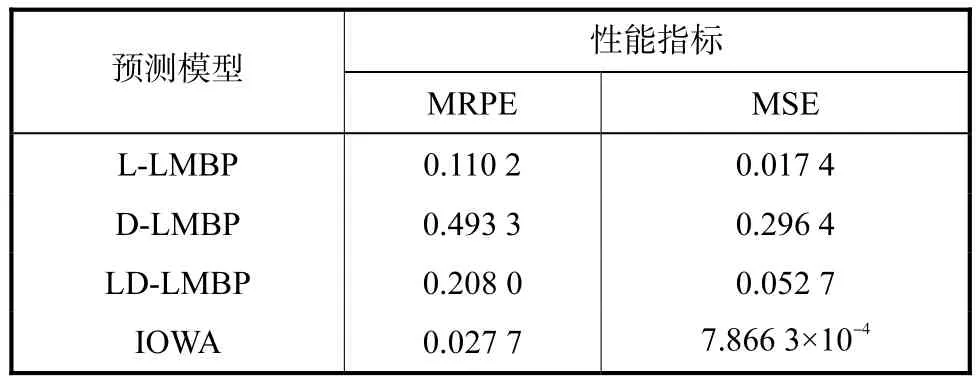
表6 预测模型预测性能对比Tab.6 MRPE and MSE for 4 different models

从表 6可以看出，L-LMBP模型、D-LMBP模型及LD-LMBP模型预测结果的平均相对误差(MRPE)和均方误差(MSE)均大于 IOWA模型的平均相对误差 2.77% 和均方误差 7.866,3×10-4．这充分说明基于IOWA算子的最优组合预测模型能够有效提高赤潮预测精度，改善预测效果．

图 3～图 6是 4种预测模型预测的浮游植物密度值与真实样本值的对比，纵坐标均为浮游植物密度，横坐标均为测试样本号．从图 3中可以看出组合模型预测值与目标值非常接近，预测效果良好；其他3种模型预测值在某些时刻误差相对较大，表明其稳定性有待提高．图 4为组合预测模型预测值与真实样本值的对比，图 5为 2种单输入的 LMBP模型预测值与真实值的对比，图 6为双输入的 LMBP模型预测值与真实值的对比．

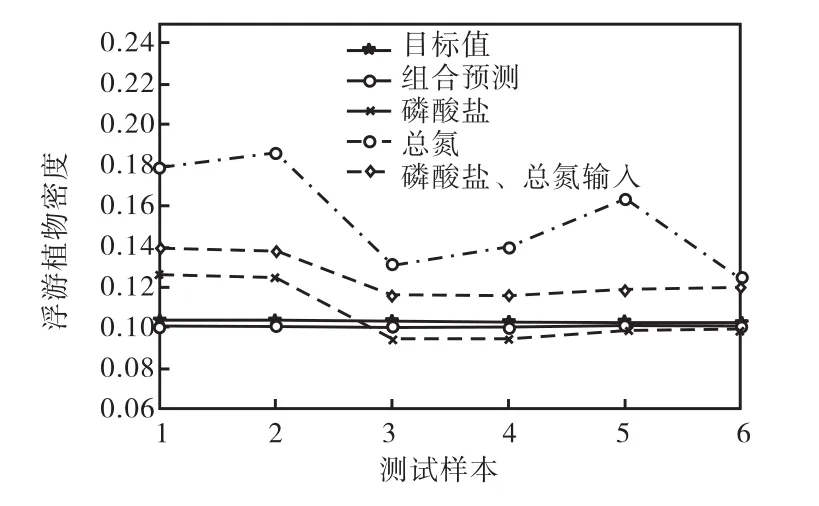
图3 4种模型预测值与真实值对比Fig.3 Comparison of real and four models predicted values

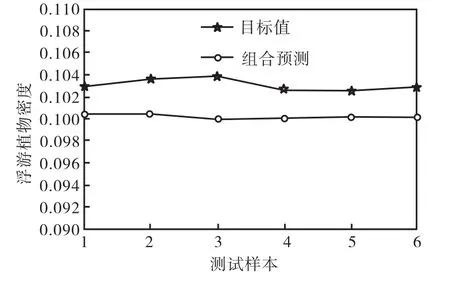
图4 IOWA预测值与真实值对比Fig.4 Comparison of real and IOWA model predicted values

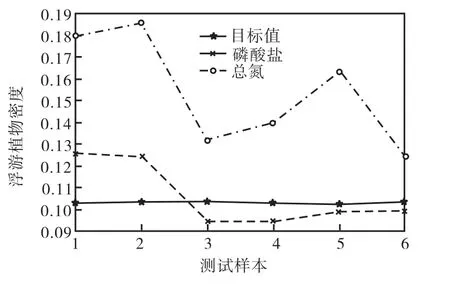
图5 L-LMBP、D-LMBP预测值与真实值对比Fig.5 Comparison of real and L-LMBP，D-LMBP predicted values

4 结 语

本文提出的赤潮组合预测模型，采用烟台四十里湾赤潮监测数据进行实验，对浮游植物密度进行预测，取得了较好的预测效果，均方误差为7.866,3×10-4，并且表明了烟台四十里湾海域赤潮的频繁爆发与磷酸盐及总氮两个理化因子密切相关．将本模型预测结果与 LMBP神经网络模型预测结果进行对比，实验结果充分证明，本文提出的组合预测模型预测更加稳定，预测精度更高．

［1］Lek S，Guégan J F. Artificial neural networks as a tool inecological modeling：An introduction[J].Ecological Modeling，1999，120(23)：65-73.

［2］Velo-Suárez L，Gutiérrez-Estrada J C. Artificial neural network approaches to one-step weekly prediction ofDinophysis acuminatablooms in Huelva(Western Andalucía，Spain)[J].Harmful Algae，2007，6(3)：361-371.

［3］Lee J H W，Yan H，Dickman M，et al. Neural network modeling of coastal algal blooms[J].Ecological Modeling，2003，159(2/3)：179-201.

［4］马玉梅，高静宇，王清华，等. 基于人工神经网络的赤潮预测模型[J]. 海洋预报，2007，24(1)：38-44.

Ma Yumei，Gao Jingyu，Wang Qinghua，et al. Forecast model for red tide on artificial neural network[J].Marine Forecasts，2007，24(1)：38-44(in Chinese).

［5］王洪礼，葛 根，李悦雷. 基于模糊神经网络(FNN)的赤潮预警预测研究[J]. 海洋通报，2006，25(4)：36-41.

Wang Hongli，Ge Gen，Li Yuelei. Research on the prediction of red tide based on the fuzzy neural network[J].Marine Science Bulletin，2006，25(4)：36-41(in Chinese).

［6］Melesse A M，Krishnaswamy J，Zhang K. Modeling coastal eutrophication at Florida Bay using neural networks[J].Journal of Coastal Research，2008，24(2)：190-196.

［7］Hagan M T，Menhaj M B. Training feedforward networks with the Marquardt algorithm[J].IEEE Trans Neural Net，1994，5(6)：989-993.

［8］Bates J M，Granger C W J. The combination of forecasts[J].Operational Research Quarterly，1969，20(4)：451-468.

［9］Yager R R. Induced ordered weighted averaging operators[J].IEEE Transactions on Systems，Man，and Cybernetics，1999，29(2)：141-150.

［10］Yager R R. Induced aggregation operators[J].Fuzzy Sets and Systems，2003，137(1)：59-69.

［11］陈华友，蔡正高. 诱导有序加权平均的组合预测模型及其应用[J]. 安徽大学学报：自然科学版，2005，29(1)：1-6.

Chen Huayou，Cai Zhenggao. Combined forecasting model based on induced ordered weighted averaging operator and its application[J].Journal of Anhui University：Natural Science Edition，2005，29(1)：1-6(in Chinese).