地基动刚度对地下管线随机地震响应的影响

王 岱，屈铁军，梁建文

(1. 天津大学建筑工程学院，天津 300072；2. 北方工业大学建筑工程学院，北京 100041)

大量地震台阵记录的研究证实，地震动在空间和时间上是随机分布和随机变化的，为此，不少学者对地下管线进行了随机地震响应分析[1-5]，文献[1]采用平面应变解求解了管线与土的相互作用，但其仅适用于埋深为无穷大的情形，文献[2-5]均采用弹性地基梁模拟管线与土的相互作用，不足之处是无法考虑频率的影响．因此，笔者利用弹性半空间动力基本解[6]，求解管线与土的动力相互作用，然后采用随机振动的虚拟激励法[7]，研究了地下管线纵向和横向的地震反应，同时采用半空间静力基本解求得管与土的静力相互作用，并进行了比较．台阵记录也证实，地震时地面上各点的地震动是部分相关的，而地面运动的这种性质对地下管线的影响还不十分清楚，因此，本文选择较为常用的3种相干模型[8-10]：Q-W-W相干模型、H-V相干模型和 L-Y相干模型，以比较部分相关性对地下管线的影响．另外，文中采用文献[11]提出的自功率谱模型和文献[8]提出的视速度模型．研究结果表明，随着埋深的增大，地基动刚度对频率的变化越来越敏感，与静刚度有明显的差别；地基静刚度可近似替代动刚度的根本原因是地面位移自功率谱的低频特性．

1 振动方程及求解

设一长直管线埋于弹性、均匀、各向同性的半无限空间中，埋深为d(指管轴线至地表的距离)且管轴线与半无限空间表面平行，管线与土之间没有滑移．连续管线的振动必须考虑管线与周围土介质的动力相互作用，振动方程中反映管线与土动力相互作用的量是和，即单位长管线周围介质的纵向、横向动刚度．

动刚度的计算采用如下的方法：假定单位均布简谐荷载作用在单位长度的管轴线上(计算纵向动刚度时，荷载方向平行于管轴线；计算横向动刚度时，荷载方向垂直于管轴线)，然后利用弹性半空间动力基本解，可以得出与荷载位置对应的参考点(如图1所示)处的位移，将所得位移沿荷载分布长度积分，便可得出平均位移，而后再倒数可得到动刚度．

当作用荷载为单位均布的静力荷载时，单位长管线周围介质的刚度则为实数，同理即可得出其静刚度

图1 与荷载位置对应的参考点Fig.1 Reference point relative to load location

1.1 纵向振动

连续管线纵向振动方程为[1]

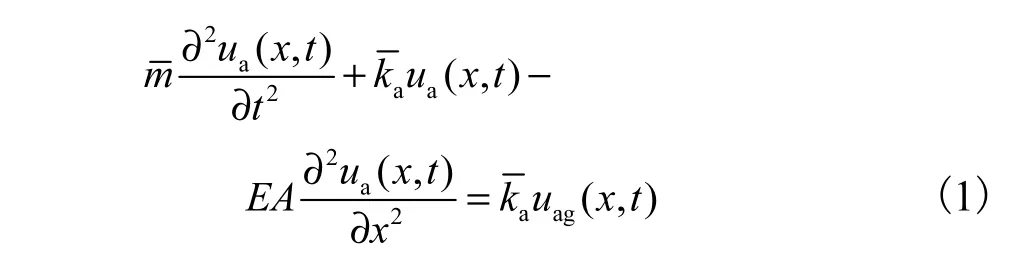
由于地下管线很长，当计算长度取得足够长时，边界条件对管线中部的影响很小，边界条件可以任意选取，这里选用图2所示的边界条件，即

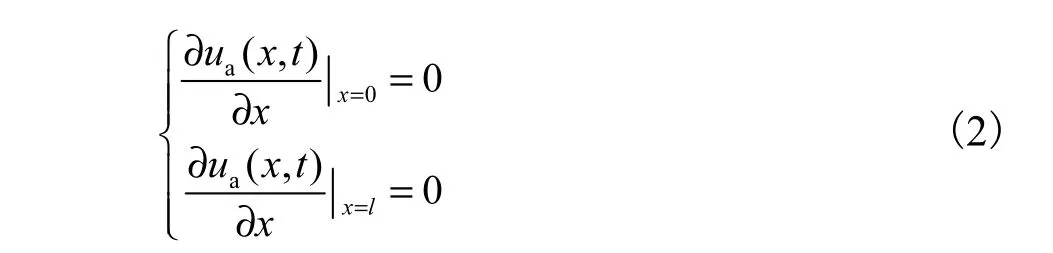
式中l为计算长度．

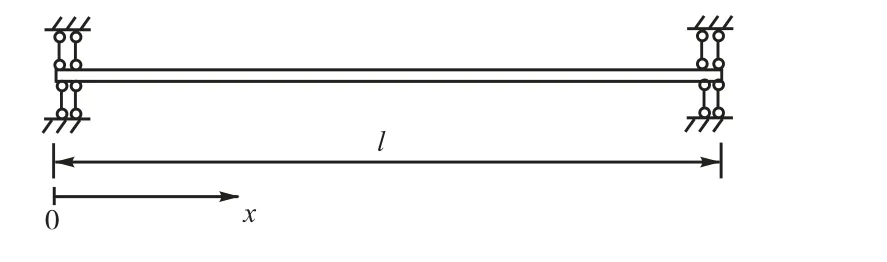
图2 纵向振动的边界Fig.2 Boundaries for axial vibration

采用振型叠加法求解式(1)，管线的总位移可表示为

由式(3)可看出，总位移是用无穷级数表示的，但实际计算时，只需取有限项数便可得到足够精确的结果，因此，假定取前 1n+项，则总位移 ua(x,t)及解耦后的广义坐标方程分别用矩阵表示为

式中变量 q上面的符号“·”表示该变量对时间求二阶导数．

由式(12)可以看出，需要对连续轴向地震激励进行积分，采用数值积分，当积分步长取得足够小时便可得到足够精确的结果．因此假设已知等间距xΔ的m个点处的时程，则可把式(12)写成

式中：F为系数矩阵；vag为m个已知时程点组成的纵向地震位移向量．

将式(14)代入式(5)，可得

利用虚拟激励法[7]求解．虚拟激励法的最大特点之一是将平稳随机振动分析转化为简谐振动分析，而且只需求出简谐运动方程的稳态解．设地面虚拟加速度激励为

式中：变量上面的符号“～”表示虚拟；L满足关系式

式中：Saa为地面加速度互功率谱矩阵；上标“*”表示共轭．则地面虚拟位移激励为

将式(19)代入式(16)，可得广义坐标的虚拟稳态解为

将式(20)代入式(4)，可得管线纵向虚拟位移

则管线的纵向位移自功率谱为

将纵向位移自功率谱对频率积分，可得纵向位移方差

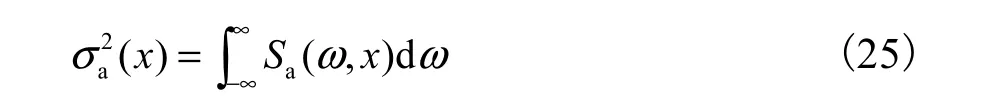
应变等其他物理量的方差同理可得．响应方差可用于极值分析等[7]．

1.2 横向振动

连续管线横向振动方程为[1]

取图 3所示的边界条件．虽然纵向振动和横向振动的运动方程和边界条件均不同，但将纵向振动解中的 E A( n πl)2改为EI( n πl)4便成横向振动情形．虚拟激励法的引入也与前所述相同，在此不再赘述．

图3 横向振动的边界Fig.3 Boundaries for lateral vibration

2 算例分析

2.1 地面激励

2.1.1 自功率谱模型

国内外诸多学者根据实际地震加速度记录给出了不同的加速度自功率谱模型，其中 Clough和Penzien提出的模型与胡聿贤给出的模型[11]比较常用．本文中选择后者，其表达式为

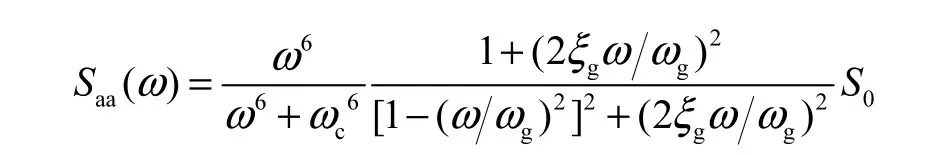
式中：ω为角频率，rad s；gω为场地土的卓越角频率，rad s；ξg为场地土的阻尼比；ωc为控制低频含量的参数，rad/s；S0为基岩加速度(白噪声)自谱密度，

2.1.2 Q-W-W相干模型

2.1.3 H-V相干模型

2.1.4 L-Y相干模型

L-Y相干模型表达式为

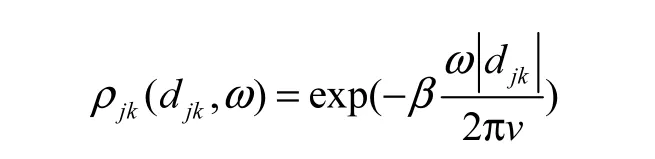
式中： β为地面运动波数；v为地震地面波视速度．参照文献[10]，取 α = 0 .125．

2.1.5 视速度模型

视速度模型表达式为

式中 c1、c2均为视速度参数．

视速度反映行波效应的影响．参照屈铁军等[8]的研究结果，c1和 c2取表1中3组数据的平均值．

假定地震持续时间为 30,s[1]．由自功率谱模型、相干函数模型及视速度模型可生成地下管线多点激励的地震输入，即互功率谱矩阵，具体过程可参见文献[12]．

表1 SMART-1台阵视速度参数Tab.1 Parameters of apparent wave velocity from Tab.1 SMART-1 array

2.2 结果分析

由于本文的地震输入是以SMART-1台阵记录为基础，而 SMART-1台阵的场地大致相当于我国抗震规范中的Ⅱ类和Ⅲ类场地[8]，因此，本文中的分析结果可供Ⅱ、Ⅲ类场地地下管道抗震设计计算时参考．

介质参数：剪切波速 cs=100 m s ，密度ρs=1.6×103kg m3，泊松比ν=0.25．

管线参数：外半径 R = 0 .25 m，壁厚 t = 0 .15R ，弹性模量 Ep= 2 .7× 1 07N m2，密度 ρp= 2 .2× 1 03kg m3．

由于管线的位移主要由刚体位移引起，且管线内力是管线抗震设计的主要依据，因此下面仅讨论管线中的应力．

图4给出了地面位移自功率谱曲线．图5为静刚度随埋深的变化，图6为动刚度的实部和虚部随频率的变化(无阻尼)．

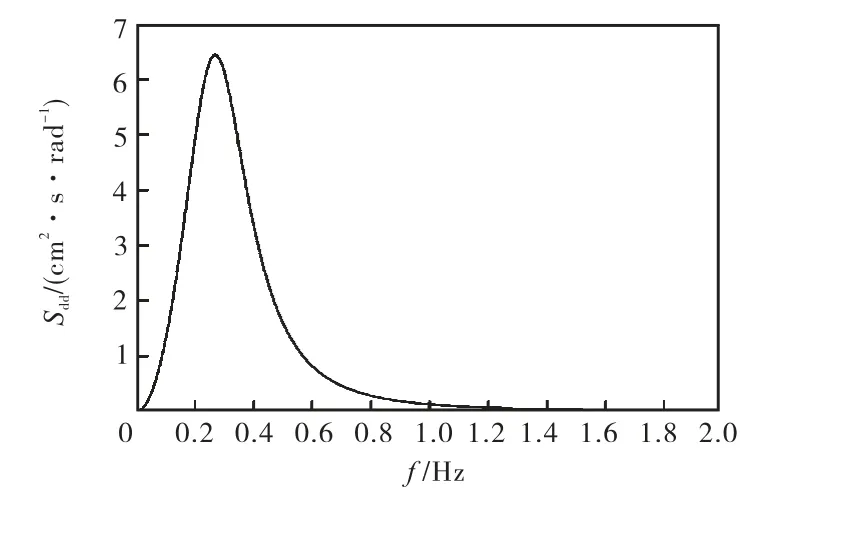
图4 地面位移自功率谱Fig.4 Auto-PSD function of ground displacement

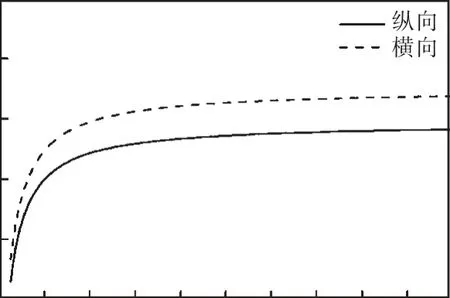
图5 静刚度随埋深的变化Fig.5 Variation of static stiffness with buried depth

一般来说，与地面位移自功率谱有效值对应的频率均在低频区，地面位移自功率谱可通过关系Saa(ω) = ω4Sdd(ω)得出，其中，Saa(ω)为地面加速度自功率谱，Sdd(ω)为地面位移自功率谱．

从图 5可以看出，随着埋深的增大，静刚度的大小逐渐趋于稳定，也就是说，当埋深大于一定值后，静刚度基本与埋深无关．

从图 6可以直观地看出，随着埋深的增大，动刚度的实部和虚部对频率的变化越来越敏感．

图6 动刚度的实部和虚部随频率的变化(无阻尼)Fig.6 Variation of real part and imaginary part of dynamic stiffness with frequency without damp

图 7给出了管线中点应力自功率谱 Sσ．可以看出，应力主要来源于低频激励的贡献，而与相干模型的选择无关．与动刚度和静刚度对应的应力自功率谱曲线几乎完全重合，其主要原因是与地面位移功率谱有效值对应的频率位于低频区．在低频区，动刚度的实部随频率的变化比较缓慢，与静刚度非常接近，同时，动刚度的虚部随频率的变化也比较缓慢，接近于零．

图 8给出了管线中点应力最大值随管线埋深的变化．将与各埋深对应的应力除以与最小埋深对应的应力，以便直观地看出应力的增幅程度．可以看出，当管线埋深到达一定值后，管中的应力基本趋于稳定，其根本原因是地面位移自功率谱分布的低频特性．同时，还可看出，相干效应对结果也有较大影响．

图 9给出了管线中点应力最大值随管外半径的变化．可以看出，当采用部分相关的地震输入时，应力随管径的增大而减小，但应力对管径变化的敏感程度因所选的相干模型的不同而存在较大差异．另外可以发现，选用 L-Y相干模型得出的结果与由完全相干得出的结果比较接近，原因是 L-Y相干模型中视速度的取值比较大，导致由 L-Y相干模型得出的相干值比较接近1．选用Q-W-W相干模型和H-V相干模型得出的结果比较接近，而且远大于选用完全相干得出的结果．

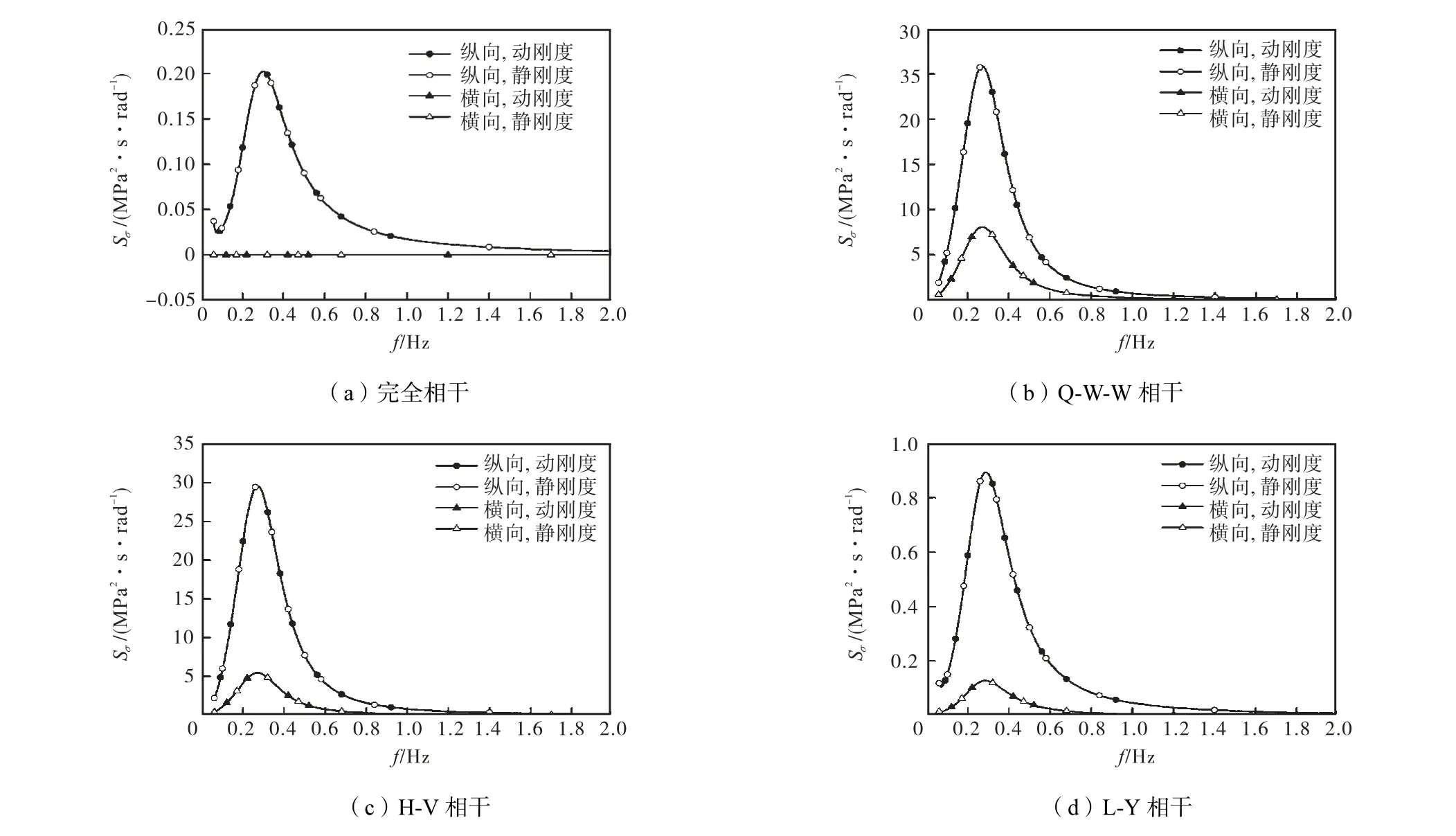
图7 管线中点应力自功率谱(d＝5 m)Fig.7 Auto-PSD function of stress in the mid-point of pipeline (d＝5 m)

图8 管线中点应力最大值随埋深的变化Fig.8 Variation of maximum stress in the mid-point of pipeline with buried depth

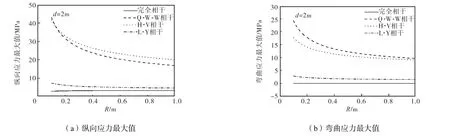
图9 管线中点应力最大值随管外半径的变化Fig.9 Variation of maximum stress in the mid-point of pipeline with pipe outer radius

3 结 论

(1) 随着埋深的增大，地基动刚度对频率的变化越来越敏感，与静刚度有明显差别．

(2) 地基静刚度可近似替代动刚度，其根本原因是地面位移自功率谱的低频特性，即地震输入的地面位移自功率谱的有效值均在低频区，而高频部分几乎为零．

本文结果可供Ⅱ、Ⅲ类场地地下管道抗震设计计算时参考．

［1］ Hindy A，Novak M. Pipeline response to random ground motion[J].Journal of Engineering Mechanics，ASCE，1980，106：339-360.

［2］ Zerva A，Ang A S H，Wen Y K. Lifeline response to spatially variable ground motion[J].Earthquake Engineering and Structural Dynamics，1988，16(3)：361-379.

［3］ 周 建，王前信. 地下管道随机反应及动力可靠性分析[J]. 土木工程学报，1993，26(4)：54-60.

Zhou Jian，Wang Qianxin. Random response and dynamic reliability analysis of underground pipeline[J].China Civil Engineering Journal，1993，26(4)：54-60(in Chinese).

［4］ 帅 健，吕英民，蔡强康. 埋地管道的平稳随机振动[J]. 石油大学学报：自然科学版，1999，23(4)：65-70.

Shuai Jian，Lü Yingmin，Cai Qiangkang. Stationary random vibrations of buried pipelines[J].Journal of the University of Petroleum，China：Edition of Natural Science，1999，23(4)：65-70(in Chinese).

［5］ 屈铁军，王前信. 地下管线在空间随机分布的地震作用下的反应[J]. 工程力学，2003，20(3)：120-124.

Qu Tiejun，Wang Qianxin. Seismic response of underground pipelines to ground motion with spatial randomness[J].Engineering Mechanics，2003，20(3)：120-124(in Chinese).

［6］ Banerjee P K，Mamoon S M. A fundamental solution due to a periodic point force in interior of an elastic halfspace[J].Earthquake Engineering and Structural Dynamics，1990，19：9-15.

［7］ 林家浩，张亚辉. 随机振动的虚拟激励法[M]. 北京：科学出版社，2004.

Lin Jiahao，Zhang Yahui.Pseudo-Excitation Method for Random Vibration[M]. Beijing：Science Press，2004(in Chinese).

［8］ 屈铁军，王君杰，王前信. 空间变化的地震动功率谱的实用模型[J]. 地震学报，1996，18(1)：55-62.Qu Tiejun，Wang Junjie，Wang Qianxin. A practical model for the power spectrum of spatially variant ground motion[J].Acta Seismologica Sinica，1996，18(1)：55-62(in Chinese).

［9］ Harichandran R S，Vanmarcke E H. Stochastic variation of earthquake ground motion in space and time[J].Journal of Engineering Mechanics，ASCE，1986，112(2)：154-175.

［10］ Loh C H，Yeh Y T. Spatial variation and stochastic modeling of seismic differential ground movement[J].Earthquake Engineering and Structural Dynamics，1988，16(5)：583-596.

［11］ 胡聿贤，周锡元. 弹性体系在平稳和平稳化地面运动下的反应[R].地震工程研究报告集. 北京：科学出版社，1962：33-50.

Hu Yuxian，Zhou Xiyuan. Response of Elastic Systems Under Stationary Ground Motion[R]. Report on Earthquake Engineering. Beijing：Science Press，1962：33-50(in Chinese).

［12］ 屈铁军，王前信. 空间相关的多点地震动合成(Ⅱ)：合成实例[J]. 地震工程与工程振动，1998，18(2)：25-32.

Qu Tiejun，Wang Qianxin. Simulation of spatial correlative time histories of multi-point ground motion(PartⅡ)：Application of fundamental formulas[J].Earthquake Engineering and Engineering Vibration，1998，18(2)：25-32(in Chinese).