A NEW WELL TEST MODEL FOR STRESS-SENSITIVE AND RADIALLY HETEROGENEOUS DUAL-POROSITY RESERVOIRS WITH NON-UNIFORM THICKNESSES*

ZHANG Lie-hui, GUO Jing-jing, LIU Qi-guo

State Key Laboratory of Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China, E-mail: zhangliehui@vip.163.com

A NEW WELL TEST MODEL FOR STRESS-SENSITIVE AND RADIALLY HETEROGENEOUS DUAL-POROSITY RESERVOIRS WITH NON-UNIFORM THICKNESSES*

ZHANG Lie-hui, GUO Jing-jing, LIU Qi-guo

State Key Laboratory of Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China, E-mail: zhangliehui@vip.163.com

(Received April 10, 2011, Revised June 30, 2011)

This article presents a new well test model for stress-sensitive composite dual-porosity reservoirs based on the concept of permeability modulus, where the rock and fluid properties as well as the formation thickness vary in the radial direction. An analytical solution in the Laplace space for the pressure-transient behavior for a line-source, constant-rate well of this type of reservoir is obtained with the Laplace transformation and the perturbation technique. The pressure and its derivative in the reservoir and the effects of relevant parameters on the pressure-transient response are obtained. The model as well as the corresponding type curves may be used in predicting the production performance or analyzing the production data for this type of reservoir.

non-uniform thickness, stress-sensitive, composite dual-porosity, well test model, type curve

Introduction

Naturally fractured reservoirs are composed of fractures with high flow and low storage capacity and a matrix with high storage and low flow capacity. The composite systems of this type of reservoirs can be encountered as a result of non-uniform fracture distribution, drilling, secondary or tertiary recovery projects, and stimulation programs. In general, a composite reservoir system is made up of two or more regions, with its own rock and fluid properties in each region.

In the past 26 years, a considerable number of theoretical studies were devoted to describe the pressure behavior of this specific type of reservoir[1-4]. In 2006, based on the previous studies, Huang and Liu[5]extended the radial composite dual-porosity model to the multi-zone condition and presented an analytical solution to describe the transient pressure behavior of a composite dual-porosity oil reservoir with non-uniform thickness and lateral heterogeneity. Zhang et al.[6]proposed a well testing interpretation model for naturally fractured reservoirs with consideration of stress sensitivity and starting pressure gradient. However, the model was only numerically solved without obtaining its analytical solution. Shan et al.[7]established a relaxation model to describe the unsteady flow of non-Newtonian visco-elastic fluid in dual-porosity media by introducing fractional order derivatives into the seepage flow. More recently, Zheng et al.[8]established mathematical models for dual porosity reservoirs with infinite outer boundary, constant pressure outer boundary and closed outer boundary, and the similar structure of the solutions in the three kinds of outer boundary conditions was analyzed. In 2009, Cai and Huang[9]presented an analytical model to describe the pressure behavior of a vertical fracture well completed in a dual-porosity composite reservoir. In 2010, with consideration of changes of the permeability modulus of fracture and using the concept of the effective stress in a pressure-sensitive dual-porosity medium, Wang et al.[10,11]developed a mathematical model of well testing for the stress-sensitive dual-porosity reservoir. In 2010, Tao et al.[12]proposed a radial compositemodel of a dual porosity inner region surrounded by a homogeneous matrix of infinite extent with consideration of the stress dependent fracture permeability. In 2011, Imad et al.[13]studied the pressure response of a multiple fractured horizontal well in a composite reservoir with a dual porosity inner zone and a single porosity outer zone, and a numerical simulator was used to examine the validity of the results. On top of that, the transient pressure distribution in dual-porosity composite reservoirs with different outer boundaries were discussed by many researchers[14,15].

The mathematical models for radial composite dual-porosity reservoirs are well developed and validated by numerous studies. However, to our knowledge, most models do not take both the permeability stress sensitivity and the formation thickness variation into account, therefore, some deviations would be resulted when they were applied to predict the pressure behavior of stress-sensitive dual-porosity reservoirs. As more and more high-pressure and low-permeability reservoirs have been discovered, it becomes necessary to establish a well test model suitable for this type of stress-sensitive reservoirs.

In this article, based on the Warren and Root’s natural fracture model, by introducing the concept of permeability modulus[16], a new well test model for stress-sensitive composite dual-porosity reservoirs is proposed, with considerations of the formation thickness and reservoir property variations in the radial direction and the simultaneous deformation of multiregion reservoirs. The analytical solution in Laplace space is obtained with Laplace transformation and perturbation technique. The type curves are plotted with Stehfest algorithm and the impacts of relevant parameters are discussed. The model as well as the method presented in this paper can be used to predict the production performance or to analyze the production data obtained from this type of well-reservoir systems.

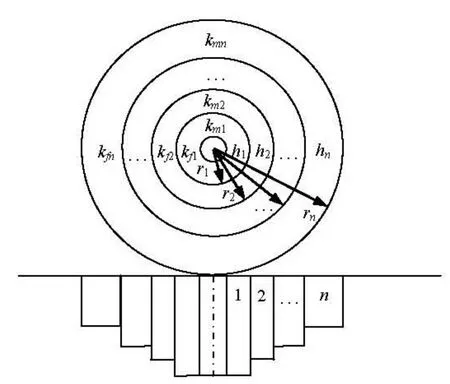
Fig.1 Schematic diagram of a multi-region and a really heterogeneous dual-porosity reservoir with non-uniform thickness

1. Mathematical model

1.1 Assumptions

The mathematical model proposed in this article is for an oil reservoir, it is also applicable to gas reservoirs by replacing the pressure term with a pseudopressure term. The mathematical model is based on the following assumptions.

(1) A dual-porosity reservoir can be divided into n concentric regions, as shown in Fig.1, in the radial direction. The rock and fluid properties of each region are different from each other. But each region is assumed to be homogeneous and isotropic with constant reservoir properties such as permeability and porosity. The reservoir thickness varies in the radial direction. The greater the n value is, the closer to the actual reservoir thickness hjit will be.

(2) Single-phase slightly compressible fluid and isothermal flowing.

(3) Reservoir properties change abruptly at the interface. Both the width and the flow resistance along the interface are neglected.

(4) Laminar flow in each zone, with negligible gravitational effect and capillary effect. The fluid flows to the well through the fracture system only, the matrix system is not connected.

(5) The well is operated in production at a constant rate with the initial reservoir pressure being pi.

(6) Stress sensitivity exists in the fracture system in each region and the permeability modulus of each region is the same.

(7) Pseudo-steady state inter-porosity flow. 1.2 Model formulation

Based on the previous assumptions and the basic theory of fluid flow in porous media, the dimensionless diffusivity equations for the fracture system and the matrix system in multi-region, stress-sensitive composite dual-porosity reservoirs can be established as follows:

The initial condition can be expressed as

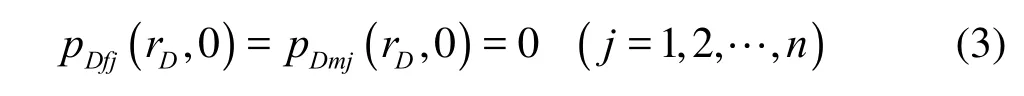
The inner boundary condition, with consideration of the wellbore storage effect and the skin effect, can be written as:

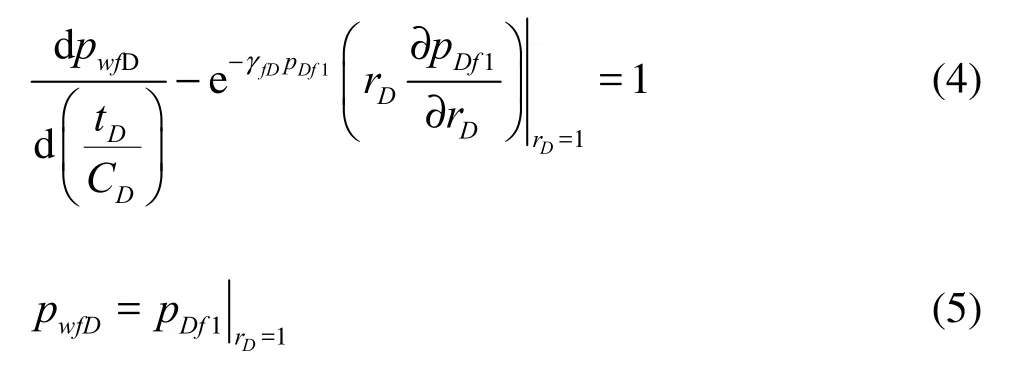
The infinite outer boundary condition can be written as

There are continuous constraints in the flow interface.

For the pressure at the interface, we have

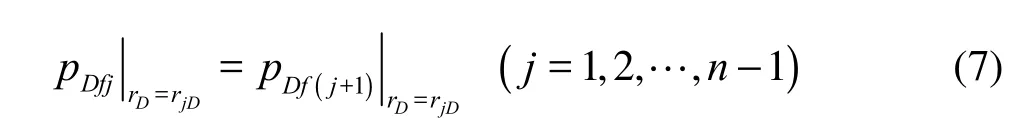
For the flow rate at the interface, we have

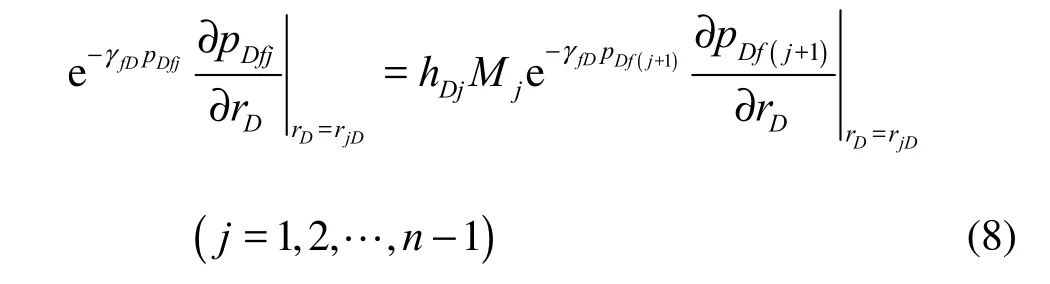
The dimensionless variables involved in the above mathematical model are defined as follows:

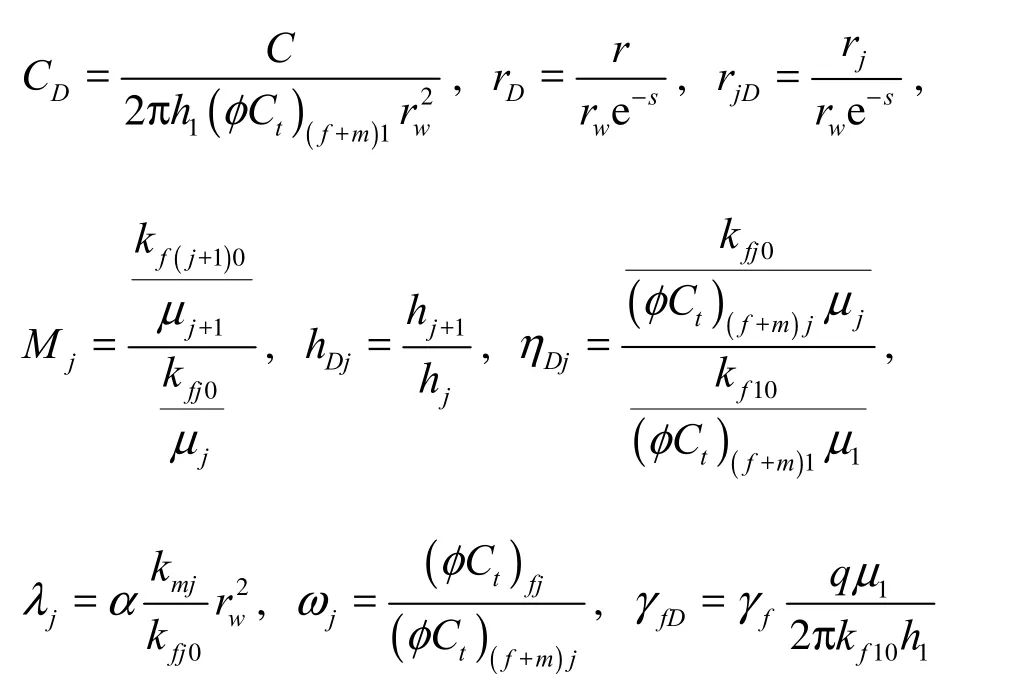
where piis the initial reservoir pressure, pwfis the bottom hole flowing pressure, pfjis the fracture pressure of region j, pmjis the matrix pressure of region j, kf10is the initial fracture permeability of region 1, km1is the matrix permeability of region 1, h1is the formation thickness of region 1, q is the sand face rate, μ1is the viscosity of fluids in region 1, pDfjis the dimensionless fracture pressure of region j, pDmjis the dimensionless matrix pressure of region j, pwfDis the dimensionless bottom hole flowing pressure, γfis the permeability modulus of the fracture system, γfDis the dimensionless permeability modulus of the fracture system, r is the radial distance, rDis the dimensionless radial distance, rwis the well radius, rjis the radius of region j, rjDis the dimensionless radius of region j, rnDis the dimensionless radius of region n, s is the skin factor, t is the production time, φf1is the fracture porosity of region 1, φm1is the matrix porosity of region 1, φfjis the fracture porosity of region j, φmjis the matrix porosity of region j, Ctf1is the total fracture system compressibility of region 1, Ctm1is the total matrix system compressibility of region 1, Ctfjis the total fracture system compressibility of region j, Ctmjis the total matrix system compressibility of region j, tDis the dimensionless time, C is the wellbore storage coefficient, CDis the dimensionless wellbore storage coefficient, hj+1is the formation thickness of region j+1, hjis the forma-tion thickness of region j, hDjis the thickness ratio, kf(j+1)0is the initial fracture permeability of region j +1, kfj0is the initial fracture permeability of region j, μj+1is the viscosity of fluids in region j +1, μjis the viscosity of fluids in region j, Mjis the mobility ratio, kmjis the matrix permeability of region j, α is the shape factor, ωjis the storativity ratio of region j, λjis the interporosity flow coefficient of region j, ηDjis the transmissibility factor ratio.

2. Model solutions

The dependence of the fracture permeability on the pore pressure makes the above seepage flow differential equations strongly nonlinear. It should first be linearized before finding the analytical solution to these nonlinear equations. We introduce the following transformation equation to linearize these equations

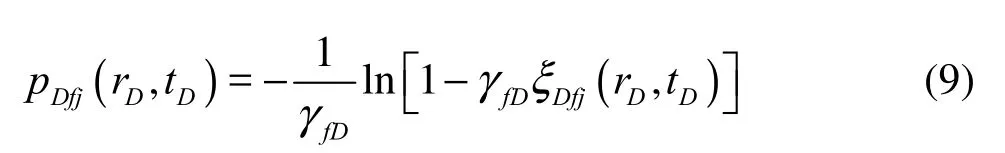
where ξDfjis a dimensionless dependent variable.

Substituting Eq.(9) into the well test model, the perturbation technique is used to simplify the equations. Because the dimensionless permeability modulus of the fracture system is usually small, the zeroorder perturbation solution is sufficient. Then the seepage flow differential equation becomes: The initial condition and the outer boundary condition are:

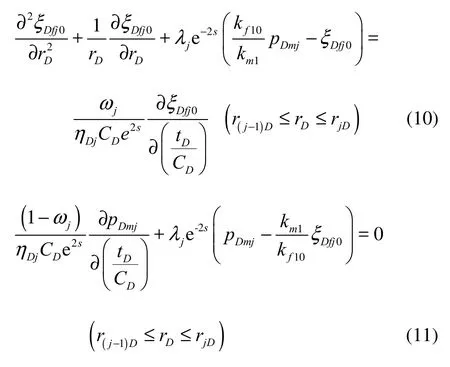
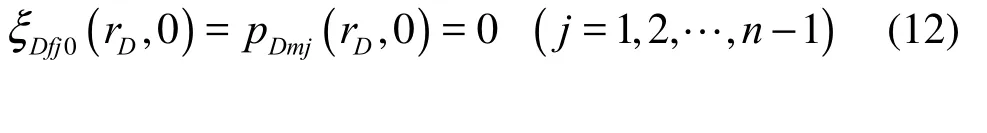
The inner boundary conditions which take into account the wellbore storage effect and the skin effect become:

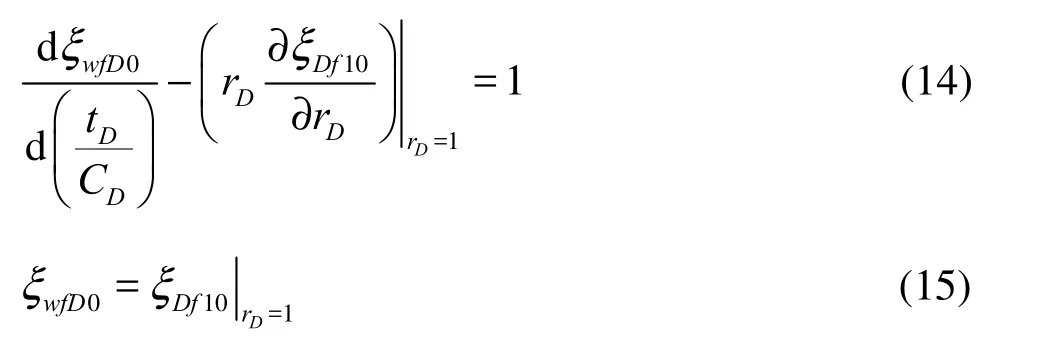
The continuous constraints at the flow interface are:

where ξDfj0,()ξ , ξDfn0, ξDf10and ξwfD0are zero-order approximations.

Combined with the initial condition (Eq. (12)), the Laplace transformations with respect to /

Dfj+1 0

t C of the flow differential equations in Eq.(10) and Eq.(11) yield

DD

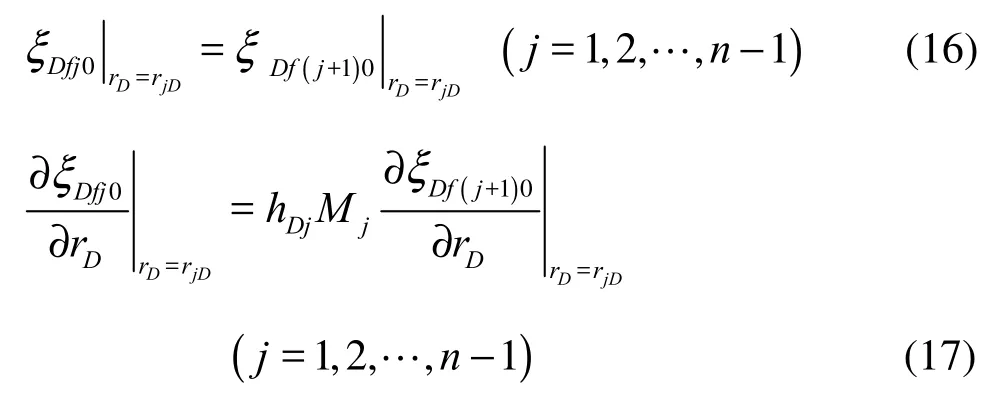
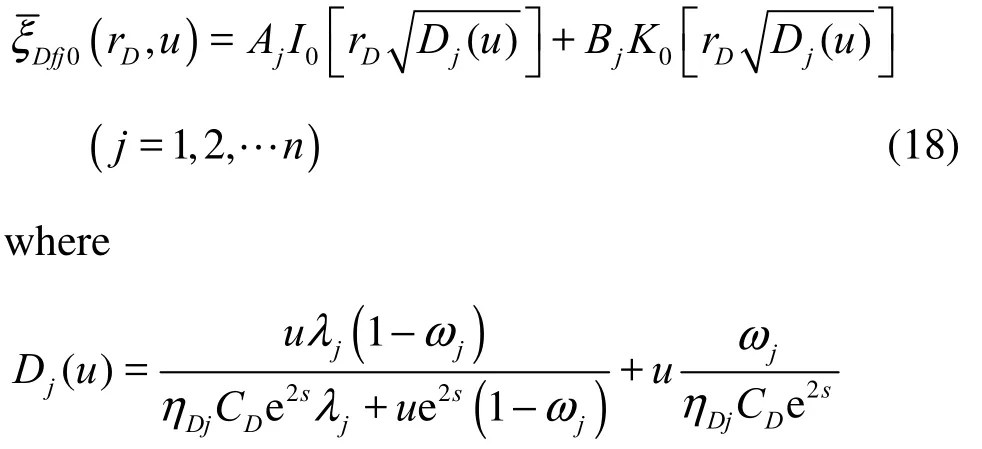
ξDfj0is the Laplace transformation of ξDfj0, u is the Laplace variable.

Combined with Eq.(18), the Laplace transformations with respect to tD/CDof Eq.(13) through Eq.(17) yield the following 2n-order linear equations

3. Plotting and analysis of type curves

The flow chart for plotting type curves is shown in Fig.2.

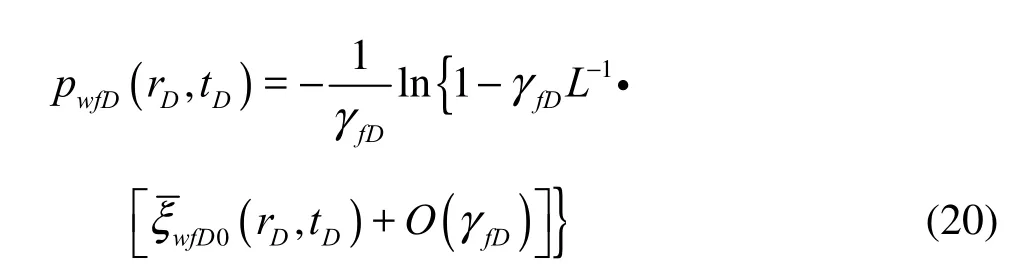
where ξwfD0is the Laplace transformation of ξwfD0, L−1is the Laplace inverse transformation.

Fig.2 Flow chart of model solving and type curve plotting

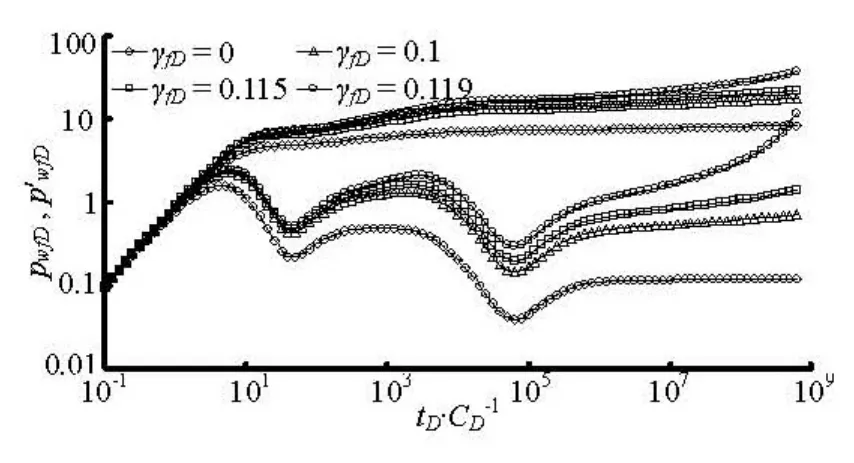
Fig.3 Type curve of a stress-sensitive composite dual-porosity

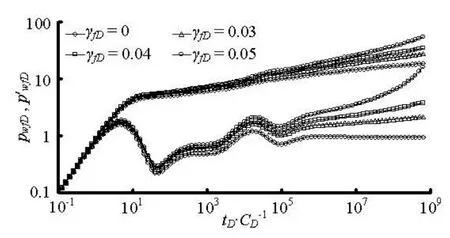
Fig.4 Type curve of a stress-sensitive composite dual-porosity

For simplicity, we plot and analyze the type curves for the case of n=2 here. However, the method proposed in this article is applicable to the cases of multiple regions.

Figures 3 and 4 show the type curves of radial heterogeneous and stress-sensitive dual-porosity reservoirs with non-uniform thickness. These figures show that the fluid flow in reservoirs can be divided into the following several stages:

(1) Wellbore storage regime. During this period, the fluid flow in the composite dual-porosity reservoir is mainly dominated by the wellbore storage effect and both the dimensionless pressure and the pressure derivative curves follow a straight line of slope of unity. The type curves corresponding to different dimensionless fracture permeability modulus values are almost the same, i.e., the dimensionless fracture permeability modulus has no effect on the shape of the type curves during the wellbore storage period.

(2) Transition flow regime after the wellbore storage regime. The duration of this period depends on the wellbore storage factor and the skin factor. During this period, the type curves with or without consideration of the effect of stress sensitivity begin to separate from each other.

(3) Fracture flow regime in the inner region, as is masked by the wellbore storage in Fig.3 and Fig.4. The derivative response goes directly from the wellbore storage hump to the transition valley, and the first 0.5 plateau is not seen.

(4) Inter-porosity flow regime in the inner region. At the transition time, an obvious valley appears in the derivative curve. Because of the permeability stress sensitivity, the depth of the characteristic valley is a function of the dimensionless fracture permeability modulus values. The valley is deeper for greater dimensionless fracture permeability modulus values.

(5) Total system flow regime in the inner region. The derivative curve is no longer stabilized on the 0.5 line, which is the characteristic of insensitive systems. As time goes on, the departure of any γfDcurve from the curve for γfD=0 increases monotonically. The extent of this deviation depends on the value of the dimensionless fracture permeability modulus. It becomes larger for greater values.

(6) Transition flow regime between the inner and outer region. The moment that this flow regime comes into being is a function of the inner region radius. With a larger r1D, the transition occurs in a later moment. The shape of the transition is a function of M1, ηD1and hD1. In addition, a more significant difference in properties between the inner and outer regions (such as mobility and thickness) would lead to a longer duration of this period.

(7) Fracture flow regime in the outer region. The dimensionless pressure derivative rises (or drops) as the outer region properties become worse (or better). This regime is masked by a transition flow regime between the inner and outer region in Fig.3 and Fig.4.

(8) Inter-porosity flow regime in the outer region. Similarly, an obvious valley can be observed on the derivative curve. The valley is deeper for greater dimensionless fracture permeability modulus values.

(9) Total system flow regime in the outer region. Similarly, the derivative curve does not follow the 0.5 stabilization line but bends upward because of the effect of fracture permeability stress sensitivity. The bigger the dimensionless fracture permeability modulus is, the more significant the bend of type curves will be. It should be noted that at a later time, if the dimensionless fracture permeability modulus is big enough, the pressure behavior of an infinite sensitive system is similar to that of a closed insensitive system (i.e., the pressure curve intersects with the pressure derivative curve).

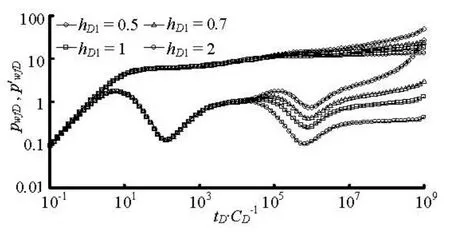
Fig.5 The effect of thickness ratio on type curves

Fig.6 Log-log fitting curves of actual well test data

Figure 5 shows the effect of outer/inner region thickness ratio on the type curves of radially heterogeneous and stress-sensitive dual porosity reservoirs when the other parameters are constant. The type curves are generated for a fixed dimensionless fracture permeability modulus, γfD=0.085. The other fixed parameters are given in the figure. As Fig.5 shows, thehigher the thickness ratio, the lower the position of dimensionless pressure derivative. A higher thickness ratio means that the supply capacity of the outer region is better than the inner region. Thus, the pressure drawdown caused by the fluid flow in the outer region is less. It also could be observed from Fig.5 that the higher the thickness ratio, the smaller the impact of the stress sensitivity on type curves.

Table 1 Fitted results

4. Discussion on parameter estimation

Well test analysis can provide useful information about reservoir characteristics. However, as it is pointed out in the literature, different parameters may have similar effects on the transient pressure responses, which may cause ambiguity in the well testing interpretation. A good combination of geological background, experiment data and production performance is required to get a more reliable explanation of the test data.

In the model proposed in this article, the interpreted permeability modulus can be verified by the stress sensitivity experiment. According to the moment that the valley occurs and its shape in the pressure derivative curve, the characteristic parameters of the dual porosity reservoirs, such as storativity ratio ωjand inter-porosity flow coefficientjλ, can be determined. The parameters related to the composite systems, such as the mobility ratio Mj, the thickness ratio hDjand the transmissibility factor ratio ηDj, can be estimated by the position of the outer zone radial flow regime relative to the inner zone radial flow regime in the pressure derivative curve. In addition, a comprehensive analysis of the log-log plot of the pressure data, the semi-log plot of the pressure data and the pressure history plot can significantly improve the reliability of parameter estimates.

5. Model validation

In this section, a production well located in a strongly heterogeneous dual-porosity gas reservoir is considered. Relevant parameters of the well are as follows. The well radius rwis 0.1 m, the reservoir thickness 10.375 m, the average porosity 0.0949, and the reservoir temperature is 84.5101oC. The well has been operated in production for 8 568 h at a rate of 128 297.4 m3/d before the pressure buildup test and the test time is 2 624 h.

The conventional composite model can not properly explain the pressure buildup data and the upward buckling of the dimensionless pressure derivative curve at a later time could not be fitted well using that model. The model established in this article, on the other hand, can explain the actual well test data to obtain satisfactory results. The log-log fitting curve is shown in Fig.6 and the fitted results are listed in Table 1.

6. Conclusions

(1) A new analytical solution for the pressuretransient behavior of a line-source well in production with a constant rate in a multi-region, radial composite dual-porosity reservoir is obtained in Laplace space, with considerations of the changes in reservoir thickness, wellbore storage effect and skin factor. It can easily be inverted into the real space, to be used in predicting the pressure performance or analyzing the test data obtained from this type of reservoir configuration.

(2) Stress sensitivity has little impact on the bottom hole pressure behavior during the early stage. The stress sensitivity begins to affect the pressure behavior (the shape of type curves) after the wellbore storage period. The dimensionless pressure derivative curves bend upward because of the fracture permeability stress sensitivity. The bigger the dimensionless fracture permeability modulus is, the more significant the bending of type curves will be.

(3) The mathematical model proposed in this article is applicable to both oil and gas dual-porosity reservoirs. It is only necessary replacing the pressure term with a pseudo-pressure term, in order to apply the model to gas dual-porosity reservoirs.

[1] LU Xiu-feng, LIU Zhen-yu and ZHAO Qiu-li et al. The theoretical analysis of heterogeneous reservoir with multi-zones by using finite element method[J]. Journal of Hydrodynamics, Ser. A, 2005, 20(5): 571-576(in Chinese).

[2] HE Ying-fu, YIN Hong-jun and LIN Mu et al. Pressure transient analysis of composite reservoir using the boundary element method[J]. Journal of Hydrodynamics, Ser. A, 2006, 21(6): 700-705(in Chinese).

[3] MENG L., LUCK D. A dual-porosity model for gas reservoir flow incorporating adsorption behaviour–Part I. Theoretical development and asymptotic analyses[J]. Transport in Porous Media, 2007, 68(2): 153-173.

[4] CHASTANET J., ROYER P. and AURIAULT J. L. Flow of low pressure gas through dual-porosity media[J]. Transport in Porous Media, 2007, 66(3): 457-459.

[5] HUANG Lin, LIU Qi-guo. Percolation mathematic model in compound gas reservoir with dual medium of excessive sections[J]. Well Testing, 2006, 15(4): 11-14(in Chinese).

[6] ZHANG Yun, WANG Zi-sheng and YAO Jun et al. Study and application of pressure transient of naturally fractured reservoirs with stress-sensitive and start pressure grade[J]. Journal of Hydrodynamics, Ser. A, 2007, 22(3): 332-337(in Chinese).

[7] SHAN Lian-tao, TONG Deng-ke and XUE Li-li. Unsteady flow of non-Newtonian visco-elastic fluid in dual-porosity media with the fractional derivative[J]. Journal of Hydrodynamics, 2009, 21(5): 705-713.

[8] ZHENG Peng-she, LI Shun-chu and ZHU Wei-bing. Similar structure of pressure distribution in double porosity composite reservoir[J]. Drilling and Production Technology, 2008, 31(4): 80-81(in Chinese).

[9] CAI Ming-jin, HUANG Zhong-xin. Pressure dynamic model of vertical fracture well in dual-porosity composite reservoir[J]. Faul-Block Oil and Gas Field, 2009, 16(3): 53-54(in Chinese).

[10] WANG Jian-zhong, YAO Jun and ZHANG Kai et al. Variable permeability modulus and pressure sensitivity of dual-porosity medium[J]. Journal of China University of Petroleum, 2010, 34(3): 80-83(in Chinese).

[11] WANG Jian-zhong, YAO Jun and WANG Zi-sheng. Pressure behavior characteristic analysis of stress-sensitive reservoirs with variable permeability module[J]. Xin Jiang Petroleum Geology, 2010, 31(3): 288-290(in Chinese).

[12] TAO Qing-feng, AHMAD G. and CHRISTINE A. Pressure transient behavior for stress-dependent fracture permeability in naturally fractured reservoirs[C]. SPE131666. Beijing, 2010.

[13] IMAD B., MEHRAN P. D. and ROBERTO A. Modeling fractured horizontal wells as dual porosity composite reservoirs–Application to tight gas, shale gas and tight oil cases[J]. SPE 144057. Anchorage, Alaska, USA, 2011.

[14] WANG Xiao-dong, ZHOU Ying-fang and LUO Wanjing. A study on transient fluid flow of horizontal wells in dual-permeability media[J]. Journal of Hydrodynamics, 2010, 22(1): 44-50.

[15] CHEN Li-ya, LI Shun-chu and LAI Xia. Solution analysis of bottom hole pressure distribution in the dual porosity composite reservoir[J]. Drilling and Production Technology, 2010, 33(5): 52-54(in Chinese).

[16] PEDROSA O. A. J. Pressure transient response in stresssensitive formations[C]. SPE 15115. Oakland, California, USA, 1986.

10.1016/S1001-6058(10)60174-6

* Project supported by the National Key Basic Research Project of China (973 Program, Grant No. 2011CB201005), the Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20105121110006) and the National Science Fund for Distinguished Young Scho- lars of China (Grant No. 51125019).

Biography: ZHANG Lie-hui (1967-), Male, Ph. D., Professor