DYNAMIC ANALYSIS OF FLUID–STRUCTURE INTERACTION OF ENDOLYMPH AND CUPULA IN THE LATERAL SEMICIRCULAR CANAL OF INNER EAR*

WU Cai-qin, HUA Cheng

Department of Mechanics and Engineering Science, Fudan University, Shanghai 200433, China, E-mail: yuwuchina@yahoo.com.cn

YANG Lin, DAI Pei-dong, ZHANG Tian-yu

Eye and ENT Hospital of Fudan University, Shanghai 200031, China

WANG Ke-qiang

Cardiovascular Disease Institute, Zhongshan Hospital of Fudan University, Shanghai 200032, China

DYNAMIC ANALYSIS OF FLUID–STRUCTURE INTERACTION OF ENDOLYMPH AND CUPULA IN THE LATERAL SEMICIRCULAR CANAL OF INNER EAR*

WU Cai-qin, HUA Cheng

Department of Mechanics and Engineering Science, Fudan University, Shanghai 200433, China, E-mail: yuwuchina@yahoo.com.cn

YANG Lin, DAI Pei-dong, ZHANG Tian-yu

Eye and ENT Hospital of Fudan University, Shanghai 200031, China

WANG Ke-qiang

Cardiovascular Disease Institute, Zhongshan Hospital of Fudan University, Shanghai 200032, China

(Received May 18, 2011, Revised September 6, 2011)

The semicircular canals, composed of lateral, anterior and posterior canals in the inner ear, are the sensors of equilibrium during head rotation movements in the three-dimensional space. Semicircular canals are filled with endolymph confined by the cupula. The study of the relationship between endolymph flow and cupular deformation is important in revealing the semicircular canals biomechanical behavior. To date, there are few studies focusing on the transient endolymph flow and cupular deformation in response to a head rotation motion. The lateral semicircular canal is mainly responsible for the sense of the horizontal rotation movement. In order to figure out the intricate dynamics in the lateral semicircular canal during the head rotation motion, the time evolutions of both endolymph flow and cupular deformation are analyzed in this article by using a fully coupled fluid–structure interaction model. It is shown that the cupular deformation provides cues for understanding the physiology of sensing the head rotation.

fluid–structure interaction, endolymph, cupula, finite element method

Introduction

Three semicircular canals are placed orthogonally in the inner ear, with the lateral canal roughly in the horizontal direction and the anterior and posterior canals in vertical directions, and they are the primary sensors for angular motions. The semicircular canals are filled with water-like liquid, endolymph. The endolymph flow used to be considered as a creeping flow in a single uniform toroidal duct[1]or a fully developed Poiseulle flow in a straight tube[2]. The previous findings were mainly related with the semicircular canal fluid mechanics but without considering the importance of cupula.

The cupula is a gelatinous partition sitting on the top of the crista and reaching to the roof of the ampullary wall. The crista is a ridge of neuroepithelial cells that traverse the ampullated end of each membranous semicircular canal. It is shown that the deformation of cupula plays an important role in the perception of the angular motion. Steinhausen (1933) considered the dynamics of the cupula-endolymph system as a highly damped torsion pendulum through a mathematical description for the sensation of the angular motion. However the damping coefficient and the time constants of the model were not determined.

The semicircular canal morphology has a great effect on the endolymph flow dynamics[3].An analysis of the endolymph flow including the effects of the utricle and the cupula was made by Van Buskirk[4]. The fluid interactions between all three ducts and thefluid flow in the ampulla were analyzed by using accurate three-dimensional mathematical models of the canals[5,6]. The displacement fields of the cupula in response to a static pressure gradient and the head rotation were obtained based on the fluid–structure interaction[7,8]. And fluid–structure interaction simulations were shown to be effective and accurate[9]. So an fluid-structure interaction analysis of endolymph and cupula during the head rotation motion would help understanding the physiological and mechanical aspects of semicircular canal.

In this article, the two-dimensional dynamic coupling between the endolymph flow and the cupula of the lateral semicircular canal is modeled by using finite element method to identify the fluid–structure interaction effects of endolymph and cupula during the whole process of the head rotation motion.

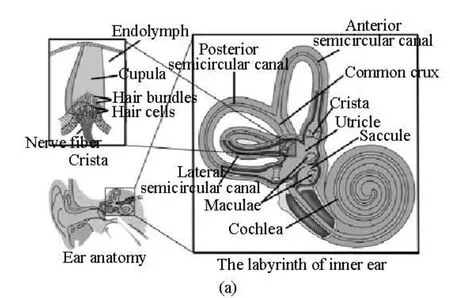
Fig.1(a) Schematic structure of the semicircular canals

Fig.1(b) A two-dimensional cross section of the lateral semicircular canal through a dashed line

1. Methods

1.1 The lateral semicircular canal model

The schematic structure of the lateral semicircular canal is shown in Fig.1, as a two-dimensional cross-section through the canal and the utricle. The geometry and all associated dimensions are obtained from the measured human data by Curthoys and Oman[3]as used by many researchers to analyze the biomechanics in the inner ear[10-12]. The canal system consists of three main regions, namely, the semicircular canal, the ampulla and the utricle. The canal is filled with endolymph. The coordinate system defined in Fig.1(b) is a global coordinate in which the canal rotates around the origin.

Table 1 Material properties of endolymph and cupula

The model consists of the endolymph fluid domain and the cupula structural domain. The flow of the endolymph is confined by the cupula, which deflects in response to the fluid pressure generated during an angular acceleration. The stiffness of the membranous tissue is some orders of magnitude greater than that of the cupula, so the membranous wall is assumed to be rigid. The material properties are listed in Table 1.

1.2 Governing equations and boundary conditions

1.2.1 Governing equations and boundary conditions for the endolymph domain The endolymph is modeled as an incompressible homogenous Newtonian fluid. The governing equations for endolymph flow are the Navier-Stokes equations, based on the principles of mass and momentum conservations as:

where u and v are the velocity fields in x and y directions, respectively, p is the pressure, and fx, fyare the body forces per unit mass, such as gravity forces. The variables x and y are the components in a cylindrical coordinate system with the origin on the canal centerline. Assume that no gravitation or other body forces affect the fluid, so fx=0, fy=0. The first equation is the equation of continuity for incompressible fluids, and the second set of equations is the momentum transport equations.

The boundary of the fluid domain is divided into the following regions: the part boundary in contact with the wall of the canal, the common crux and thefluid–structure interaction interface. The fluid in contact with the wall of the canal rotates at the same angular velocity of the canal, which is locally equivalent to a no-slip condition. The common crux is open to large volumes of fluid so the endolymph can both enter and leave the domain on its boundary, while on the fluid–structure interaction interface the velocities are equal to the deformation rate.

1.2.2 Governing equations and boundary conditions for the cupula

The cupula is considered as an elastic material and modeled as in plane-strain state. The equation of equilibrium is:

wherexσ,yσ are the normal stresses and τxyis the shear stress.

Hooke’s Law states that the strains are proportional to the stresses in this elastic material:

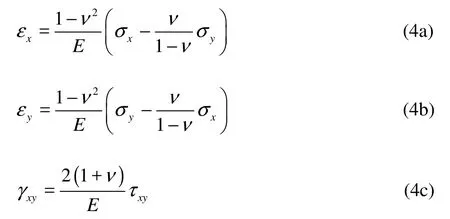
wherexε ,yε are the normal strains, γxyis the engineering shear strain.

The relationship between cupular strains and displacements is,

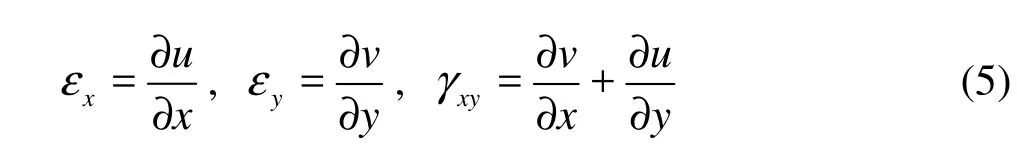
where u and v are displacements in the x and y directions, respectively.

For boundary conditions, the cupula is fixed to the top and bottom of the semicircular canal. The rotational angular velocity of the canal is imposed on the top and bottom. All other cupular boundaries serve as the fluid-structure interface.

1.2.3 The fluid-structure interaction of endolymph and cupula

The fluid flow would lead to the deformation of the structure. This deformation, in turn, changes the boundary conditions for the fluid flow. The fluid–structure interaction force f exerted by the fluid on the solid boundary is given by

where n is the normal vector to the boundary, I denotes the unit diagonal matrix. This force represents the combination of pressure and viscous forces.

In order to effectively make sure that the fluid flow domain is changed along with the structural deformation of the cupula, an Arbitrary Langrangian-Eulerian moving mesh is used for the model.

1.3 Simulation conditions

The 2-D lateral semicircular canal model is designed and used in simulations with the finite-element analysis software Comsol Multiphysics 3.5a, on intel® Xeon® CPU X3323 @2.5Ghz, with main memory of 8GB. The head rotation is assumed to be around the center of the canal. Figure 2 shows the angular velocity applied to the lateral semicircular canal. The canal rotates clockwise first. The angular velocity (ω) applied to the canal increases rapidly to a steady-state value of/2 rad/s at 0.2 s. The canal begins to rotate anticlockwise from 2.4 s and arrives to the origin at 4 s.

Fig.2 Angular velocity of the lateral semicircular canal

2. Results

2.1 Endolymph flow and cupular displacement during rotational motion

Figure 3 shows the evolution of the endolymph flows and its impact on the cupular volume displacement during the head rotational motion. The cupula deflects in the opposite direction of the rotation near the bottom base of the cupula at the instant of 0.05 s (Fig.3(a)). The cupula returns back to its resting position due to its elastic properties at the instant of 0.34 s (Fig.3(b)). When the canal begins to return to its initial position, the endolymphatic flow forms vorticesin the ampulla at t=2.4s (Fig.3(d)) and t=4s (Fig.3(f)). When the rotational motion is stopped, the cupula is deflec ted in th e sa me direction as the first deflection at theonsetoftherotationalmotiondueto the fluid inertia and reaches the maximum value of about 65 μm at t =3.93s (Fig.3(e))

Figure 4 shows the fluid velocity relative to the wall of the canal along the line MN. The line MN crosses the slender part of the canal as shown in Fig.4(a). It can be seen that the endolymph flow relative to the wall of the canal becomes a Poiseuille flow at 0.016 s after the beginning of the head rotation (Fig.4(b)).

Figure 5 shows the flow velocity of point P, the middle point of line MN, during the head rotation. The endolymph flow velocity increases and decreases rapidly at the first 0.2 s and becomes constant from 0.25 s to 2 s. The flow velocity slows down to zero at 2.4 s and turns to negative in the opposite direction. The fluid velocity rises to the maximum value at 3.2 s and is decreased down to zero at 4 s again.

2.2 Cupular shear strain during rotational motion

Figure 6 shows the shear strain of the cupula during the rotational motion. The largest shear strain of the cupular is predicted to appear at the top of the crista and then down to the sloping flanks of the crista during the head rotation. It reaches a maximum value of about 0.16 s at 0.12 s. At 2 s, the negative maximum shear strain is reached near the top of the crista. As the time goes on, the maximum shear strain returns to the top of the crista again at t=4s.

Fig.3 Time sequences of endolymph velocity and cupula volume displacement fields during a rotation motion.

3. Discussions

The interaction of endolymph and cupula at a constant angular velocity or transcupular fluid pressure was investigated by many reseachers[5,7,14]. However there were few studies focusing on the endolymph flow and the cupular deformation during all stages of the rotation motion using the finite element analysis. In this study, a two-dimensional dynamics of the fluid–structure interaction of endolymph and cupula in the lateral semicircular canal during the head rotation motion is analyzed using the finite element method.

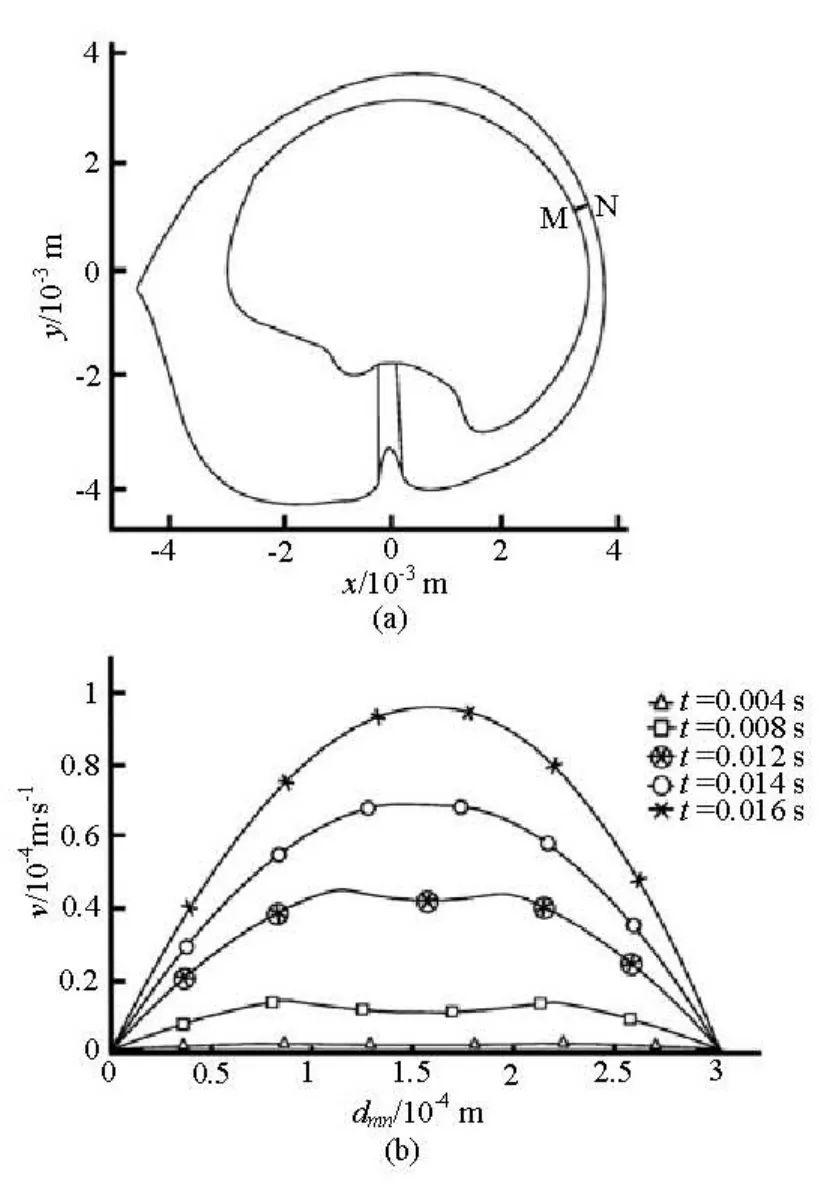
Fig.4 Velocity profile of the fluid flow relative to the wall of the canal in the slender part of the canal at the beginning of the head rotation

In our model, the fluid in contact with the wall of the canal is assumed to move with the velocity of the canal according to the no-slip condition, while all other fluid in the canal may lag behind the motion of the canal. The lagged flow fluid of the endolymph in the lateral semicircular canal leads to the cupular deflection. After the canal rotates with a constant speed, the cupula returns to its resting position. This result is consistent with the previous study[15]. The sensation of the rotation progressively diminishes and eventually disappears as the cupula gradually returns to it resting position.

The endolymph flow is identified as a Poiseuille flow at 0.016 s after the beginning of the head rotation, which can serve as a basic validity of our model. The endolymph flow in the utricle is disturbed by an abrupt change of the angular velocity, and the disturbances lead to the formation of vortices in the utricle at 2.4 s and 4 s when the canal rotates in an opposite direction and stops suddenly. The cupular volume displacements during the vortex formation are also larger than that at a constant speed. It is the fluid–structure interaction of the endolymph and the cupula that stimulates the hair cells to generate nerve impulses so that sudden change of an angular velocity can be sensed.

Fig.5 The flow velocity of point P during the head rotation

The cupular volume displacement at the beginning of the head rotation is shown near the bottom base of the cupula close to the slope part of the crista. The volume displacement position of the cupula is the same as that in the experiments with indian-ink injections[16]. Because the cilia of hair cells are generally longer at the slope part of the crista[17], they can be bended by a very small cupular displacement to produce nerve impulses at the initial head rotation. The maximum cupular volume displacement during the rotation is near the center of the cupula, and similar results were obtained by previous studies[8,18].

The maximum shear strain occurs near the top surface of the crista where the shorter cilia are located when the canal is accelerated or decelerated, and spreads down the sides of the crista where the longer cilia locate during the constant speed period. The maximum shear strain distribution is similar to that in response to static and changing transcupular pressures[7,18]. Because the cilia of hair cells extend into the cupula, the shear strain of the cupula is the critical factor for the mechanosensitive transduction channelin the hair cells[19]. The cupular shear strain plays an important role in the deflection of the hair cell cilia during the head rotation. The mechanical stimulus of the cilia is actually determined by the cupular shear strain rather than the cupular volume displacement.

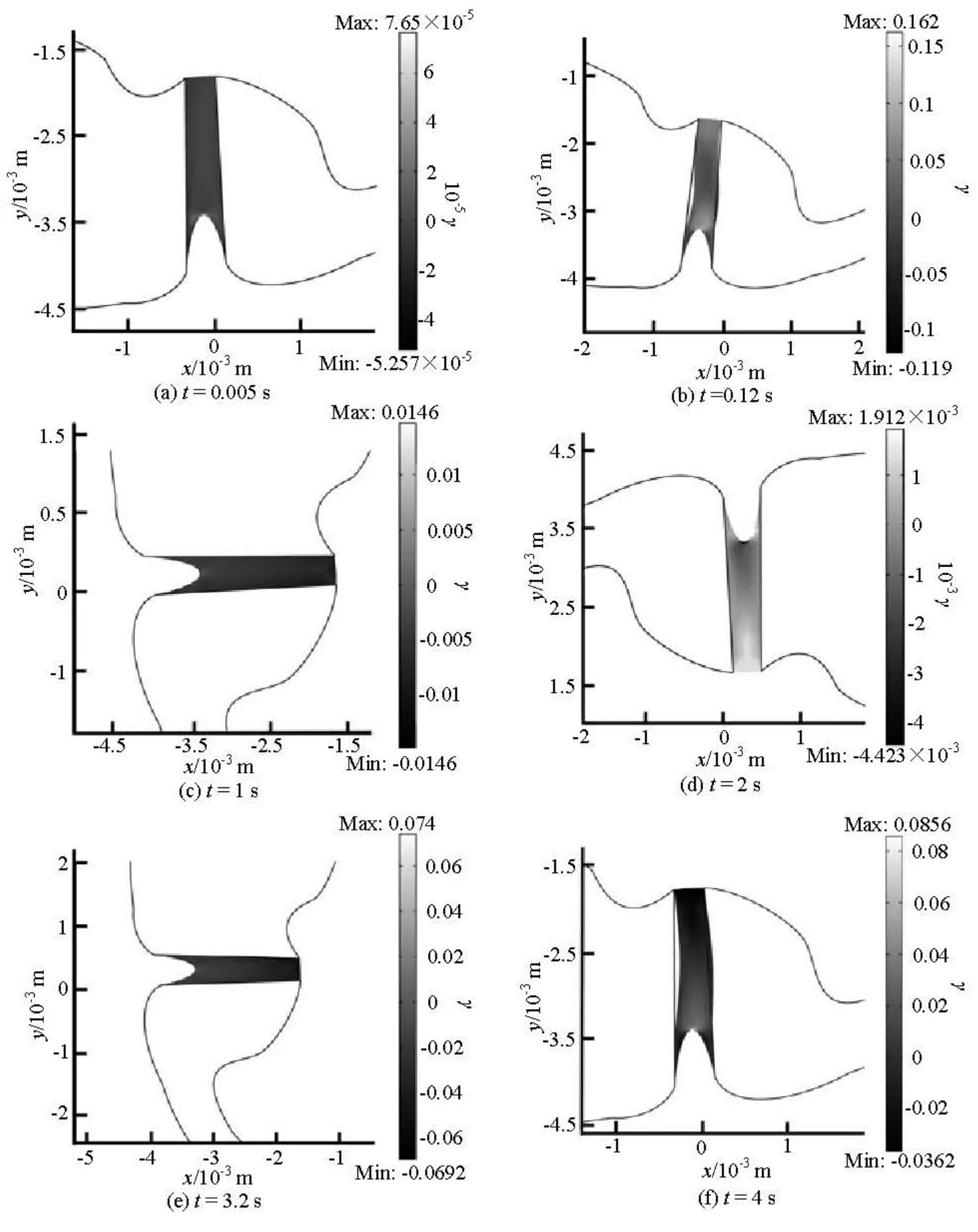
Fig.6 The shear strain (γ) of the cupula at different instants during the head rotation

4. Conclusions

In this article, a two-dimensional computational model of the lateral semicircular canal is constructed using the FEM method. Dynamic behaviors of the fluid-structure interaction between endolymph flow and structural deformation of the cupula during the head rotation motion are simulated. Our simulation results show that:

(1) The endolymph flow pattern is shown to be a Poiseuille flow after the beginning of the head rotation, which may serve to verify the model. The endolymph flow forms vortices in the utricle when the canal begins to return its initial position and when the head rotation stops.

(2) The maximum cupular volume displacement is near the center of the cupula and the maximum shear strain occurs near the location of the cilia during the rotation. The mechanical stimulus of the cilia is actually determined by the cupular shear strain rather than the cupular volume displacement.

In the present work, the endolymph flow characteristics and the cupular elastic deformations are investigated qualitatively. Combining the anatomy of lateral semicircular canal and the clinical symptoms, a further quantitative analysis of the interaction betweenthe endolymph and the cupula in the inner ear, involving the endolymph vorticity, the cupular displacement and the stresses or strains, can provide useful insights on the temporal coding of the angular head movements.

Acknowledgement

This work was supported by the Graduate Innovation Fund of Fudan University (Grant No. EYH2126023).

[1] BOSELLI F., OBRIST D. and KLEISER L. Comparison of the flow patterns in healthy and pathological vestibular systems[C]. The euromech colloquium 521. Zurich, Switerland, 2011, 63-64.

[2] BOSELLI F., OBRIST D., and KLEISER L. A meshless boundary method for computation of stokes flow with particles in the semicircular canals of the inner ear[J]. Proceedings of Mathematics and Mechanics, 2010, 10(1): 459-460.

[3] CURTHOYS I. S., OMAN C. M. Dimensions of the horizontal semicircular duct, ampulla and utricle in the human[J]. Acta Otolaryngologica, 1987, 103(3-4): 254-261.

[4] VAN BUSKIRK W. C. The effect of the utricle on fluid flow in the semicircular canals[J]. Annals of Biomedical Engineering, 1977, 5(1): 1-11.

[5] RAJGURU S. M., IFEDIBA M. and RABBITT R. D. Three-dimensional biomechanical model of benign paroxysmal positional vertigo[J]. Annals Biomedical Engineering, 2004, 32(6): 831-846.

[6] DAMIANO E. R., RABBITT R. D. A singular perturbation model of fluid dynamics in the vestibular semicircular canal and ampulla[J]. Journal of Fluid Mechanics, 1996, 307: 333-372.

[7] YAMAUCHI A., RABBITT R. D. and BOYLE R. et al. Relationship between inner-ear fluid pressure and semicircular canal afferent nerve discharge[J]. Journal of the Association for Research in Otolaryngology, 2002, 3(1): 26-44.

[8] SELVA P., MORLIER J. and GOURINAT Y. Toward a three-dimensional finite-element model of the human inner ear angular accelerometers sensors[J]. International Journal for Computational Vision and Biomechanics, 2010, 3(2): 149-156.

[9] CHOI Choeng Ryul, KIM Chang Nyung. Direct numerical simulations of the dynamics of particles with arbitrary shapes in shear flows[J]. Journal of Hydrodynamics, 2010, 22(4): 456-465.

[10] KASSEMI M., DESERRANNO D. and OAS J. G. Fluid-structural interactions in the inner ear[J]. Computers and Structures, 2005, 83(2-3): 181-189.

[11] VEGA R., ALEXANDROV V. V. and ALEXANDROVA T. B. et al. Mathematical model of the cupulaendolymph system with morphological parameters for the axolotl (ambystoma tigrinum) semicircular canals[J]. The open medical informatics journal, 2008, 26(2): 138-148.

[12] SADEGHI S. G., GOLDBERG J. M. and MINOR L. B. et al. Effects of canal plugging on the vestibuloocular reflex and vestibular nerve discharge during passive and active head rotations[J]. Journal of Neurophysiology, 2009, 102(5): 2693-2703.

[13] KASSEMI M., DESERRANNO D. and OAS J. G. Effect of gravity on the caloric stimulation of the inner ear[J]. Annals of the New York Academy of Sciences, 2004, 1027(1): 360-370.

[14] CIARAVELLA G., LASCHI C. and DARIO P. Biomechanical modeling of semicircular canals for fabricating a biomimetic vestibular system[C]. Conference Proceedings: 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. New York, 2006, 1758-1761.

[15] DAVIS J. R., JOHNSON R. and STEPANEK J. et al. Fundamentals of aerospace medicine [M]. Philadelphia, USA: Lippincott Williams and Wilkins, 2008, 172.

[16] TEN KATE J. H. The mechanics of the growing semicircular canal[J]. The Journal of Experimental Biology, 1973, 58(2): 351-366.

[17] SUZUKI M. Functional physiology of the semicircular canal ampulla[J]. Biological sciences in space, 2001, 15(4): 353-355.

[18] SELVA P., OMAN C. M. and STONE H. A. Mechanical properties and motion of the cupula of the human semicircular canal[J]. Journal of Vestibular Research, 2009, 19(3): 95-110.

[19] HIGHSTEIN S. M., POPPER A. N. and FAY R. R. The Vestibular System[M]. New York: Springer-Verlag, 2004, 153-201.

10.1016/S1001-6058(10)60176-X

* Project supported by the National Natural Science Foundation of China (Grant No. 30971528), the Shanghai Committee of Science and Technology of China (Grant No. 10ZR1403500).

Biography: WU Cai-qin (1979-), Female, Ph. D. Candidate

DAI Pei-dong, E-mail: peters818@yahoo.com.cn