FACTORS INFLUENCING BENDING RIGIDITY OF SUBMERGED VEGETATION*

WU Long-hua, YANG Xiao-li

College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China, E-mail: jxbywlh2000@yahoo.com.cn

FACTORS INFLUENCING BENDING RIGIDITY OF SUBMERGED VEGETATION*

WU Long-hua, YANG Xiao-li

College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China, E-mail: jxbywlh2000@yahoo.com.cn

(Received November 11, 2011, Revised June 5, 2011)

The bending rigidity of submerged vegetation is closely related with vegetative drag force. This work aims at determining the effects of flow conditions and characteristics of vegetation on the bending rigidity of submerged vegetation. Based on the dimensional analysis method, the factors influencing the bending rigidity of individual submerged vegetation were analyzed. The relationship between the relative bending rigidity and its influencing factors was investigated by experimental observation, and a relative bending rigidity expression for submerged vegetation was obtained by means of multiple linear regression method. The results show that the submerged vegetation has three states under different inflow conditions, and the each critical relative bending rigidity of individual submerged vegetation was determined for the different states of submerged vegetation.

cross section shape coefficient, submerged vegetation, relative bending rigidity, vegetation Reynolds number, vegetation Froude number

Introduction

Aquatic plant is an important part of a river ecosystem, and an effective tool for protection and restoration of water eco-environment[1,2]. In the river bank, aquatic plant has many functions, including protecting soil, preventing soil erosion, developing and protecting banks by its developed root. On the other hand, the flow structure is changed by the caudex and leaf of vegetation in the river, the roughness of river bank is increased, and flood drainage capacity of river courses is weakened[3-6]. And aquatic plant further changes the regulations of pollutant transportation, sediment deposition, and fluvial process. In recent years, the relationship between aquatic plants and hydrodynamic characteristics has been one of the hotspots that the domestic and oversea researchers pay much attention to.

The influence mechanism of aquatic plant on flow is very complicated, which is not only dependent on the cross sectional shape of river, water depth, discharge, but also on the species, bending rigidity, distribution, shape of vegetation and whether it is submerged[7]. In accordance with the relationship between flow conditions and vegetation’s characteristics, aquatic plants can be divided into rigid and flexible vegetations, or submerged and non-submerged vegetations. Previous researchers have carried out a large amount of researches on the experiment and theory for flexible and rigid vegetation respectively, and a lot of significant achievements are got in this field. White and Nepf[8]made use of the stick to simulate rigid vegetation, and vegetative drag, turbulence, and diffusion were studied in detail by laboratory and field observations. Subsequently, Nepf and Vivoni[9]further studied the flow structure in depth-limited vegetated flow. This study describes the transition between submerged and emergent regimes based on three aspects of canopy flow: mean momentum, turbulence, and exchange dynamics. Righetti and Armanini[10]researched the resistance due to vegetation in a river characterized by fully submerged vegetation formed by concentrated colonies of bushes, and a model was proposed based on time and spatial averaging. Musleshand Cruise[11]used the rigid rods to simulate the rigid unsubmerged vegetation, and the effects of flow depth, velocity, rod diameter, lateral spacing, and longitudinal spacing were estimated. Shi and Li[12]studied the vertical profiles, relative shear velocities and Manning roughness coefficients under different water depths, discharges and aquatic vegetation densities. For flexible vegetated flow, Yuji et al.[13]measured and analyzed the longitudinal and vertical velocity components of the flow field with a two-component laser-Doppler velocimetry. Characterization of flow resistance (friction factors) due to vegetation flexible roughness for different plant density was attained according to flume experimental[14]. The influences of vegetation concentration and the ratio of depth and height of vegetation were analyzed, and the relationship between the velocity distribution and the turbulence intensity distribution was also analyzed[15]. Applying the π-theorem and the incomplete self-similarity condition, Carollo et al.[16]deduced a flow resistance equation which links the friction factor with the shear Reynolds number, the depth-vegetation height ratio and the inflection degree.

Based on the quasi-theoretical analysis, the resistance equation of vegetated channel flow is obtained by Kouwen[17]

where U is average velocity, u∗is shear velocity, C1is represented by the vegetation density and relative roughness coefficient, C2is represented by vegetation rigidity, AVis the vegetation area in cross section, A is cross section areas of channel.

The plastic slices were used to simulate the flexible vegetation, and the Eq.(1) is tested by laboratory flume experiments. The experimental result of Kouwen[17]is afresh analyzed by other researcher. An interesting phenomenon was obtained, it has three different areas in vegetated flow, and they are almost entirely over, waggle and perpendicularity respectively. Samani and Kouwen[18]studied the flexible plastic roughness in channel flow, and calculated C1and C2in Eq.(1), giving their values in between 0.15 and 0.25. One of them holds true for the fluctuation or perpendicularity of vegetation, and the other holds true for over vegetation.

However, rigid or flexible aquatic plant is related to both the characteristics of vegetation and the inflow conditions. under different inflow conditions, the rigid or flexible would be transformed each other. Previous researchers are focusing on the impacts of the aquatic plant on the flow, while the influence of the flow on characteristics of aquatic plant has been neglected. Vegetation on floodplains is commonly assumed to behave as rigid roughness that can lead to large errors in the relationships between velocity and drag force[19,20]. So, in the present work, applying dimensional analysis method (the π-theorem), the influencing factors of the bending rigidity of individual submerged vegetation are analyzed, and the influence mechanics of inflow conditions are discussed for the bending rigidity of individual submerged vegetation by experimental data.

1. Theoretical analyses

The bending rigidity of submerged vegetation is defined as[9]

where E is the elastic modulus of submerged vegetation. I is the moment of inertia of neutro-axis.

The bending rigidity of submerged vegetation is relevant to a lot of factors, but the most important factors are inflow characteristics and vegetation itself. Consequently, the bending rigidity of submerged vegetation can be described as

where ρ is the water density, μ is the dynamic viscosity, V is the depth-averaged velocity, Asis the cross-section area of submerged vegetation’s caudex, HVis the height of submerged vegetation. At the same time, HValso represents the direct affected area of flow on the submerged vegetation in the water depth direction.

For the individual submerged vegetation, the elastic modulus (E) is presumed constant, when its projective width of perpendicular to the flow direction keeps unchanged, the bending rigidity can be rewritten as

Here T is the length of submerged vegetation along the flow direction.

Based on the dimensional analysis, Eq.(4) can be transformed as

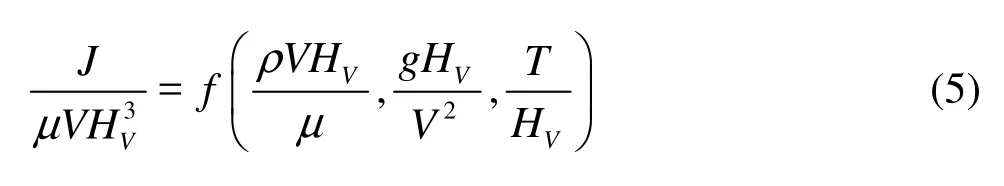
or in a simpler form

where RJis the relative bending rigidity of submerged vegetation, and it reflects inflow conditions and characteristics of submerged vegetation (include bending rigidity and height). Re∗is the Reynolds number for submerged vegetation, Fr∗is the Froude number for submerged vegetation, SCis cross section shape coefficient of submerged vegetation, and they are defined as, respectively:

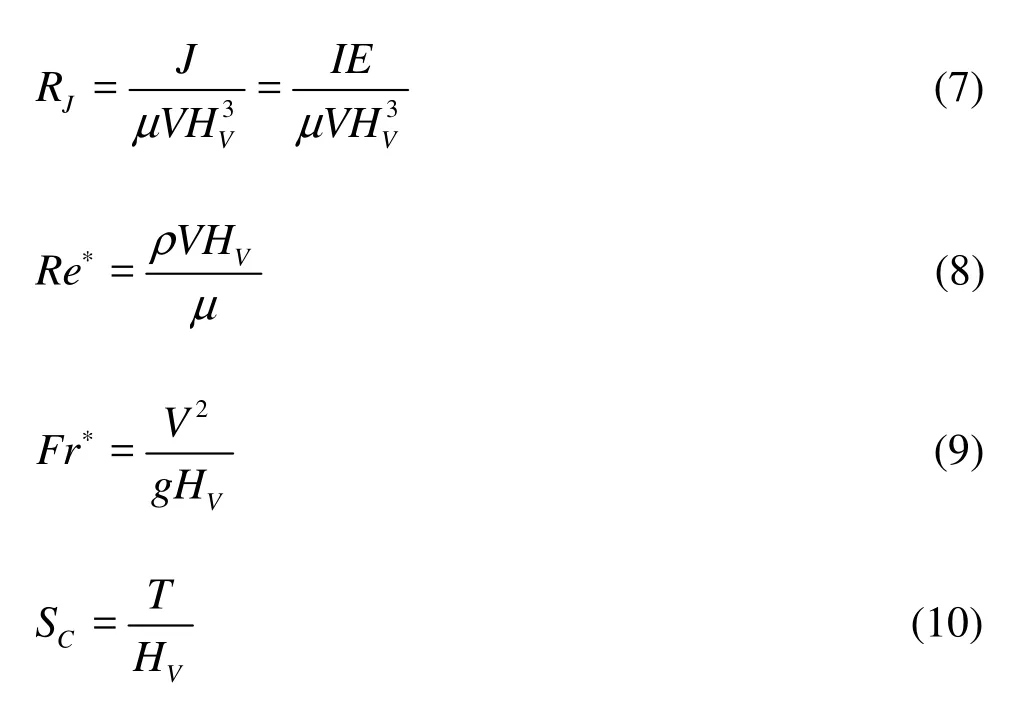
where RJ, Re∗, Fr∗and SCare all dimensionless parameters. Equation (7) shows that the relative bending rigidity of submerged vegetation (RJ) has negatively exponential correlation with the averaged velocity and the height of submerged vegetation.

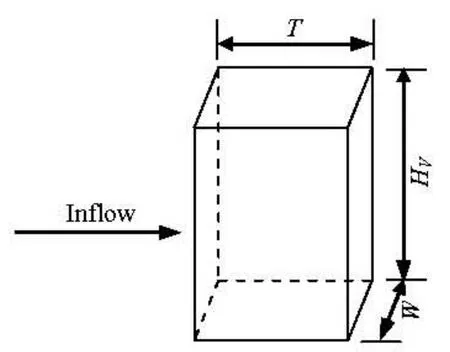
Fig.1 Sketch of plexiglass flake

2. Experimental procedures

2.1 Simulation of submerged vegetation

Because the caudex of submerged vegetation projection in flow direction is rectangle, the plexiglass flake was used to simulate the caudex in the experiments, E =0.27× 103MPa . The cross section of plexiglass is shown in Fig.1, in which W is the width of flake, and T is the thickness of flake. In these experiments, the width of flake is 0.03 m, and the thickness has three classes, 5×10–4m, 2×10–3m and 5×10–3m respectively. These different thicknesses are used to simulate different cross section shape coefficient of submerged vegetation. The moment of inertia of neutro-axis is given by

2.2 Experimental setup and conditions

Experiments were conducted in a smooth glass rectangular open-channel, which is 10.00 m long, 0.295 m wide and 0.45 m deep, and the bed slope of the flume can be adjusted to keep steady uniform flow. The channel system consists of pump, inlet, static pond, energy dissipation grid, experimental channel, tail gate, measuring weir and recycling tank (Fig.2(a)). Water is supplied from recycling tank by pump, and then flow into the open-channel. To keep the water flow stable, water needs to flow through static pond and energy dissipation grid. The stable water state reaches the experiment requirement. The water depth was adjusted by the tail gate installing at the end of the flume. The flow discharge was measured by the rightangled thin triangular weir. Submerged vegetation was located in the centeal part of cross section of the glass flume, as shown in Fig.2(b), in which x, y, z denote the longitudinal, transverse and vertical axes, respectively.

In the present work, all experiments were carried out under the uniform flow conditions. So, the mean velocity can be calculated by

where Q is the total flow rate, AFthe total flow area, B the width of glass flume, H the water depth.

Six cases have been examined for every cross section of submerged vegetation. These experiments were conducted by changing water depth, flow discharge and the height of submerged vegetation. All experimental parameters for every case are shown in Table 1.

3. Experimental results and analysis

The relative bending rigidity (RJ), Reynolds number (Re∗), Froude number (Fr∗), cross section shape coefficient (SC) of submerged vegetation and average velocity were calculated by Eqs.(7)-(12) in Sections 1 and 2. It is observed in the present experiments that the submerged vegetation shows three different states, and they are almost entirely over,

Fig.2 Sketch of experimental setup

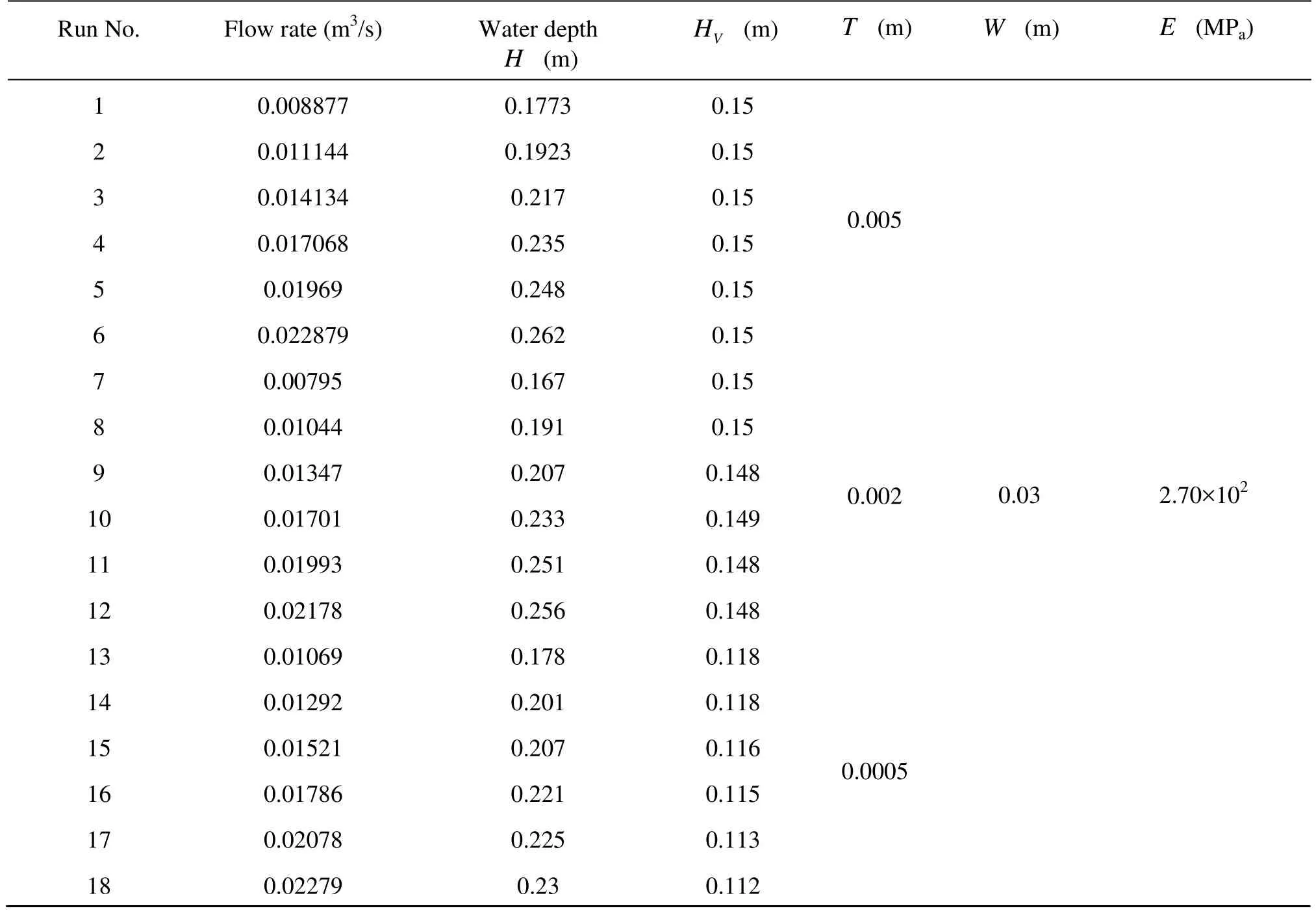
Table 1 Experimental conditions for the runs considered

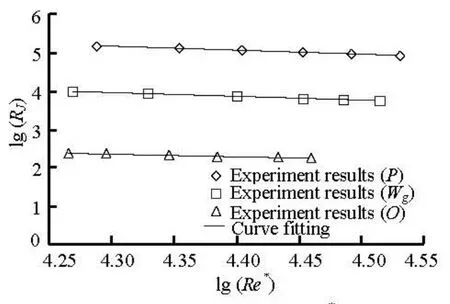
Fig.3 Relation between RJand Re∗

waggle and perpendicularity. This is consistent with the results by Kouwen[17]. Hereinafter, the letters P, Wgand O will be used to represent the submerged vegetations’ state respectively.

3.1 Impact of Reynolds number Re∗

For the different states and Reynolds number of submerged vegetation, the relative bending rigidity of submerged vegetation is given in Fig.3.

The relationships between the relative bending rigidity and Reynolds number of submerged vegetation were determined, which are listed as follows:where2

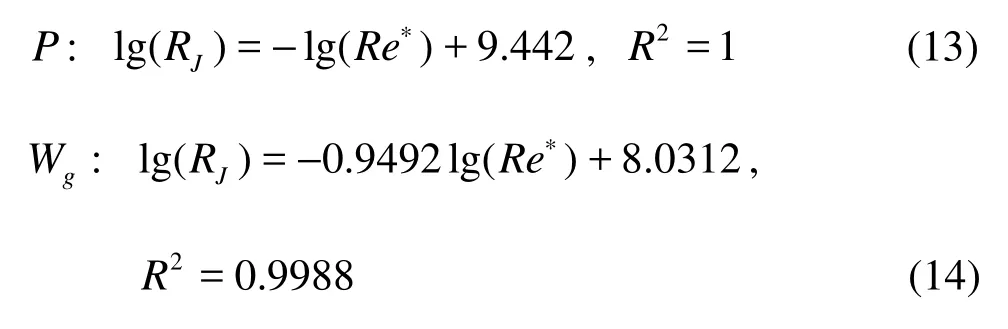
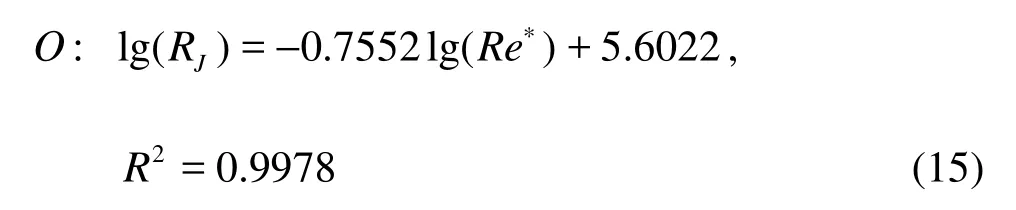
R is correlation coefficient of the above fitting equations, which proves the accuracy of the expression.

It can be seen from Fig.3 that the relative bending rigidity of submerged vegetation decreases with increasing Reynolds number Re∗for every state of submerged vegetation. Equations (13)-(15) show that the relation between the denary logarithm of Re∗and denary logarithm of RJis a negative linear correlation. For the different state of submerged vegetation, the relationships between lg(RJ) and lg(Re∗) can be expressed as a unitive one

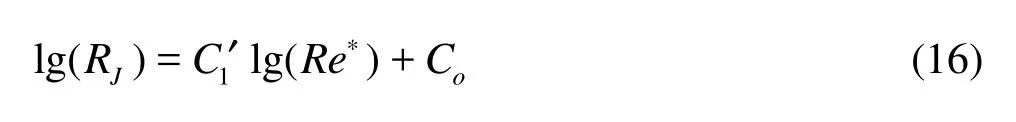
where C1′ and Coare the dimensionless integration constants.

3.2 Impact of Froude number Fr∗

For the different states and the Froude number of submerged vegetation, the relative bending rigidity of submerged vegetation is shown in Fig.4.

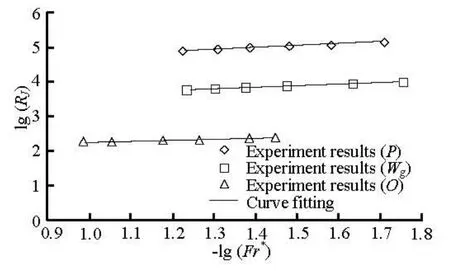
Fig.4 Relation between RJand Fr∗

Figure 4 shows that the relative bending rigidity decreases with the increase of the Froude number Fr∗for every state of submerged vegetation. For different states of submerged vegetation, the function is gotten by data fitting respectively.

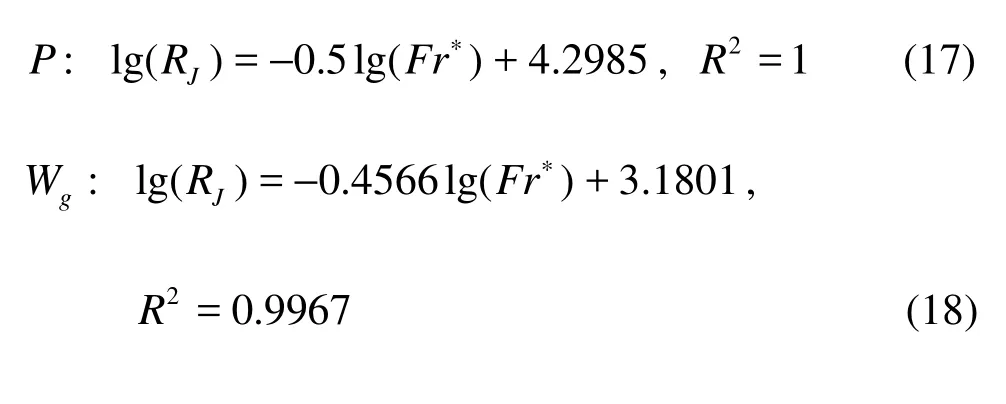
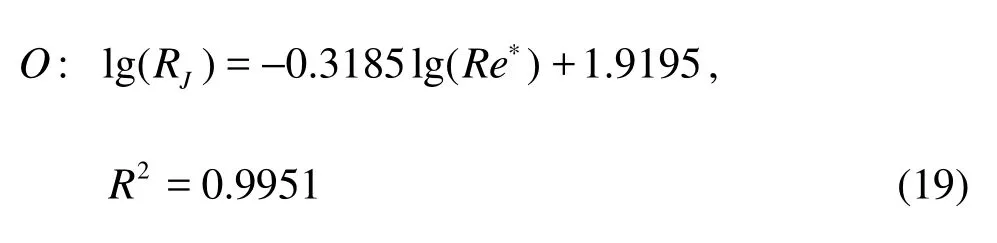
Equations (17)-(19) all show that the relation between the lg(Fr∗) and the lg(RJ) is also a negative linear correlation. Thus, the relationship between lg(RJ) and lg(Fr∗) is given as a unitive one

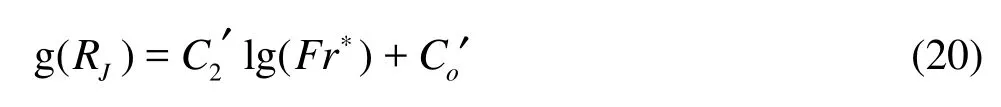
where C2′ and Co′ are dimensionless integration constants.

3.3 Impact of cross section shape coefficient SC

For the different average velocities of inflow and cross section shape coefficients of submerged vegetation, the relative bending rigidity of submerged vegetation is shown in Fig.5.

Fig.5 Relation between RJand SC

The relationships between the relative bending rigidity and cross section shape coefficient of submerged vegetation were determined for V=0.22 m/s−0.27 m/s

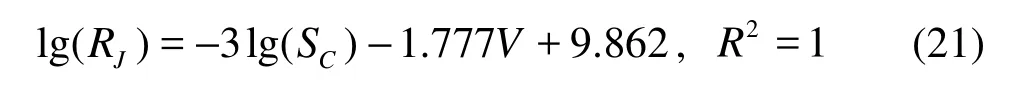
It can be seen from Fig.5 that the relative bending rigidity increases with the cross section shape coefficient SCfor every state of submerged vegetation. Equation (21) shows that the relation between the denary logarithm of RJand the denary logarithm of S is a linear correlation. So, Eq.(21) can be unitively described as

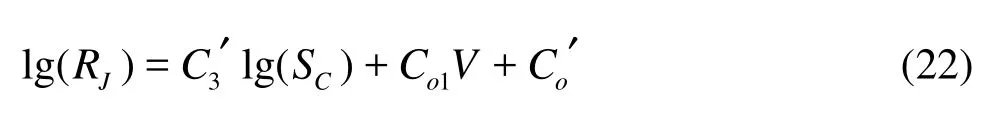
where C3′, Co1and Co′are all dimensionless integration constants.

3.4 Integration function

Quantitative analysis of each factor on the relative bending rigidity of submerged vegetation was conducted, and the above results show that the denary logarithm of RJhas a linear correlation with the denary logarithm of the Re∗, Fr∗and SC. Therefore, a hypothesis is proposed by

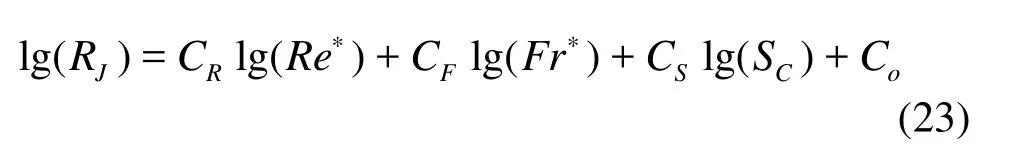
where CR, CF, CSand Coare the dimensionless integration constants, which are determined by inflow conditions and submerged vegetation itself respectively.

Based on the experimental data and multiple linear regression method, the unknown constants CR, CF, CSand Cocan be obtained by SPSS, given as

where F is the test of significance, and P is the corresponding probability.

Then, Eq.(23) can be rewritten as

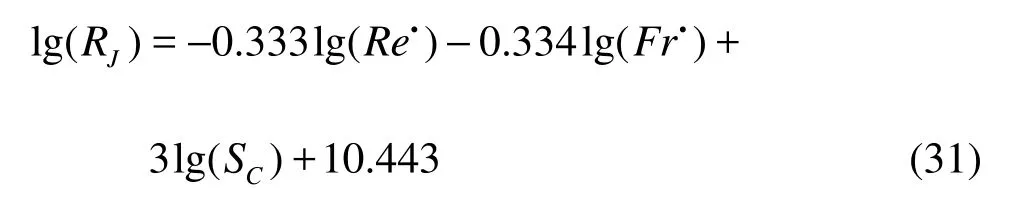
The values of F and P show that regression equation is effective, and its fitness is very good.

The above results are gotten for the submerged vegetation, but they can be applied either to submerged vegetation or to emergent vegetation, and it only needs to change height of submerged vegetation into the local water depth in the above equations.

3.5 Critical relative bending rigidity

For the different states of the submerged vegetation and the average velocity of inflow, the relative bending rigidity of submerged vegetation is shown in Fig.6.

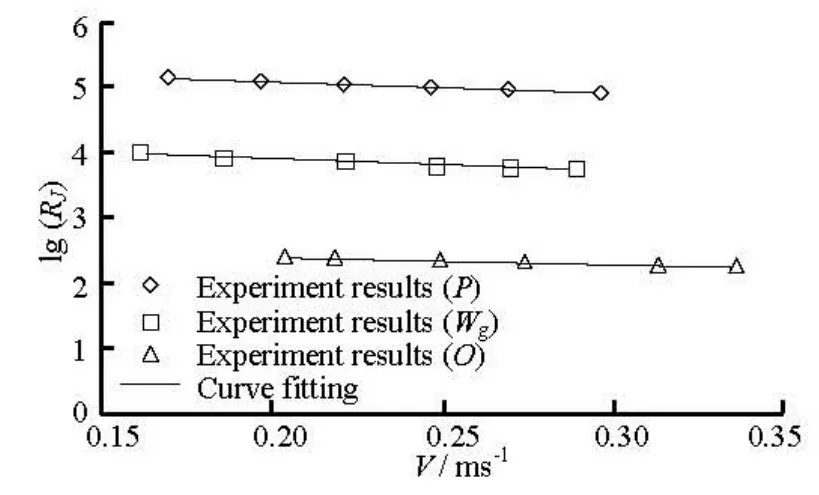
Fig.6 Relation between RJand V

The fitting functions are obtained for different states of submerged vegetation, which are listed as follows:

It can be seen from Fig.6 that the relative bending rigidity decreases as the average velocity of the inflow increases for every state of submerged vegetation, and it is consistent with Eq.(7). On the other hand, Eqs.(32)-(34) indicate that the relation between the denary logarithm of RJand the average velocity of the inflow is a negative linear correlation.

Equation (34) shows that the maximum value of the lg(RJ) is 2.5993. Consequently, if lg(RJ)＜2.5993, the submerged vegetation can be thought of as completely flexible, otherwise, the submerged vegetation is non-flexible. In Eq.(33), the maximum value of lg(RJ) is 4.2669. Then, if lg(RJ) ≥ 4.2669, the submerged vegetation can be thought of as completely rigid. When 2.5993 ＜ lg(RJ) ＜ 4.2669, the submerged vegetation is in the transition state from the completely flexible to completely rigid. That is to say, the submerged vegetation is in a state of waggle.

4. Conclusions

The factors influencing the bending rigidity of individual submerged vegetation have been studied in this article. The following conclusions could be drawn:

(1) The relative bending rigidity of submergedvegetation decreases with increasing Reynolds number and Froude number of submerged vegetation, and increases as the cross section shape coefficient of submerged vegetation increases. The relation among lg(RJ) and lg(Re∗) and lg(Fr∗) is a negative linear correlation. Otherwise, the relation between lg(RJ) and lg(SC) is a linear correlation.

(2) Based on experimental results and the multiple linear regression analysis, a relative bending rigidity expression for submerged vegetation is obtained

This expression reflects the comprehensive influences of three factors mentioned above, and it could describe the vegetation states under flow conditions and characteristic of vegetation.

(3) The different critical values of lg(RJ) is obtained for the different states of submerged vegetation. If lg(RJ) ＜ 2.5993, the submerged vegetation could be considered as completely flexible, otherwise, it is non-flexible. If lg(RJ) ≥ 4.2669, the submerged vegetation could be deemed as completely rigid. When 2.5993 ＜ lg(RJ) ＜ 4.2669, the submerged vegetation is in a state of waggle.

The above results are obtained for the submerged vegetation, but they are applicable not only to submerged vegetation, but also to emergent vegetation, and one only needs change height of submerged vegetation into the local water depth in the above equations. The difference of the submerged vegetation resistance is very striking on the different states, and the resistance characteristics of the submerged vegetation will be further spelled out in another article.

[1] WU Zhen-bin, QIU Dong-ru and HE Feng et al. Effects of rehabilitation of submerged macrophytes on nutrient level of a eutrophic lake[J]. Chinese Journal of Applied Ecology, 2003, 14(8): 1351-1353(in Chinese). [2] YANG Ming, WU Xiao-gang and ZHANG Wei-hao et al. Application of aquatic plant in ecological restoration of eutrophic water[J]. Environmental Science and Technology, 2007, 30(7): 98-102(in Chinese).

[3] WU Fu-sheng, JIANG Shu-hai and YANG Xue-lin. Characteristics of 2D-vortex field in open channel flow with submerged rigid vegetation[J]. Chinese Journal of Hydrodynamics, 2010, 25(1): 8-15(in Chinese).

[4] LAOUNIA N. Study of the flow through non-submerged vegetation[D]. Ph. D. Thesis, Nanjing: Hohai University, 2005.

[5] WANG Pei-fang, WANG Chao and ZHU David Z. Hydraulic resistance of submerged vegetation related to effective height[J]. Journal of Hydrodynamics, 2010, 22(2): 265-273.

[6] CHEN Gang, HUAI Wen-xin and HAN Jie et al. Flow structure in partially vegetated rectangular channels[J]. Journal of Hydrodynamics, 2010, 22(4): 590-597.

[7] WU Fu-sheng, WANG Wen-ye and JIANG Shu-hai. Hydrodynamics development in vegetated open channel[J]. Advances in Water Science, 2007, 18(3): 456-461(in Chinese).

[8] WHITE B. L., NEPF H. M. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel [J]. Water Resources Research, 2008, 44(1): W01412.

[9] NEPF H. M., VIVONI E. R. Flow structure in depthlimited, vegetated flow[J]. Journal of Geophysical Research, 2000, 105(C12): 28547-528557.

[10] RIGHETTI M., ARMANINI A. Flow resistance in open channel flows with sparsely distributed bushes[J]. Journal of Hydrology, 2002, 269(1-2): 55-64.

[11] MUSLESH F. A., CRUISE J. F. Functional relationships of resistance in wide flood plains with rigid unsubmerged vegetation[J]. Journal of Hydraulic Engineering, 2006,132(2): 163-171.

[12] SHI Zhong, LI Yan-hong. Experimental studies of mean velocity profiles in vegetated river flow[J]. Journal of Shanghai Jiaotong University, 2003, 37(8): 1254-1260(in Chinese).

[13] YUJI T., SYUNSUKE I. and KENTARO K. et al. Effects of flood flow on flood plain soil and riparian vegetation in a gravel river[J]. Journal of Hydraulic Engineering, 2005,131(11): 950-960.

[14] VELASCO D., BATEMAN A. and REDONDO J. M. et al. An open channel flow experimental and theoretical study of resistance and turbulent characterization over flexible vegetated linings[J]. Flow, Turbulence and Combustion, 2003, 70(1-4): 69-88.

[15] CAROLLO F. G., FERRO V. and TERMINI D. Flow velocity measurement in vegetated channels[J]. Journal of Hydraulic Engineering, 2002,128(7): 664-673.

[16] CAROLLO F. G., FERRO V. and TERMINI D. Flow resistance law in channels with flexible submerged vegetation[J]. Journal of Hydraulic Engineering, 2005, 131(7): 554-564.

[17] KOUWEN N. Effect of riparian vegetation on flow resistance and flood potential–Discussion[J]. Journal of Hydraulic Engineering, 2000, 126(12): 954.

[18] SAMANI J. M. V., KOUWEN N. Stability and erosion in grassed channels[J]. Journal of Hydraulic Engineering, 2002, 128(1): 40-45.

[19] HUI Er-qing, HU Xing-e and JIANG Chun-bo et al. A study of drag coefficient related with vegetation based on the flume experiment[J]. Journal of Hydrodynamics, 2010, 22(3): 329-337.

[20] NIKORA V., LARNED S. and NIKORA N. et al. Hydraulic resistance due to aquatic vegetation in small streams: Field study[J]. Journal of Hydraulic Engineering, 2008, 134(9): 1326-1332.

10.1016/S1001-6058(10)60169-2

* Project supported by the Fundamental Research Funds for the Central Universities (Grant Nos. 2010B01514, 2010B01314) the National Natural Science Foundation of China (Grant No. 51179057).

Biography: WU Long-hua (1974-), Male, Ph. D., Associate Professor