桥上无砟轨道无缝道岔挠曲力模型试验研究

刘泳钢，张丽平，杨荣山

(西南交通大学 高速铁路线路工程教育部重点实验室，成都 610031)

无缝道岔是实现跨区间无缝线路的关键技术之一。随着我国铁路客运专线的大力建设，无缝道岔开始铺设于桥上无砟轨道上。无缝道岔是比无缝线路的受力和变形更加复杂的轨道部件［1］。简支梁桥上无缝道岔受力条件非常复杂，梁在列车荷载作用下产生挠曲变形，简支梁上翼缘收缩，下翼缘伸长，梁的各截面产生转角，引起上下翼缘纵向位移。由于梁的一端为固定支座，下翼缘的伸长将受到固定支座的约束，当梁挠曲时，梁各截面的位移，实际上是梁的平移和旋转的组合。当上翼缘发生位移时，它通过桥面结构与轨道的联结，使扣件阻力作用于钢轨，从而带动钢轨位移。此时钢轨在纵向分布阻力作用下将产生纵向力，即挠曲力［2］。由于列车荷载并不是直接作用在梁上，其传力方式是道岔—轨道板—梁—墩［3］。由此可知，在列车荷载作用下，道岔和轨道板的关系、轨道板和梁的关系以及墩台位移等都需要进行深入研究，以便弄清桥梁与无缝道岔的相互作用关系，为建立桥上无缝道岔计算理论提供依据，继而指导桥上无缝道岔设计。

1 试验方案

1.1 试验概况

通过对一组铺设在3×32 m无砟简支梁桥上的客运专线18号道岔进行荷载加载模型试验，研究挠曲力在荷载加载过程中的变化规律以及产生的挠曲力对桥上无缝道岔、轨道板、梁体等结构的影响。依据相似三定律进行模拟试验，该桥上无缝道岔模型比例为1∶3。钢轨采用8 kg/m轻轨，扣件为重新设计的扣板式扣件，限位器和间隔铁采用Q235钢轧制而成。岔下无砟轨道基础采用纵连板式无砟轨道，用钢板单孔箱型梁模拟混凝土梁，以实体钢轨模拟荷载作用，将其均匀放置在道岔模型结构上。试验模型见图1，分别对简支梁桥的1号墩固定和4号墩固定的两种工况进行了挠曲力测试，图中从右至左依次为1号墩～4号墩。

图1 试验模型实图

1.2 试验原理

在挠曲力计算时，不考虑轨面制动力和桥梁的温度变化，桥梁在竖向荷载作用下的挠曲位移、道岔钢轨在温度力作用下的伸缩位移和设有伸缩调节器后的轨条伸缩位移为主动荷载［3］。挠曲力的计算基本假设:①梁的纵向位移按两跨梁上作用的荷载计算。②前一荷载位置下的挠曲力对后一位置下的挠曲力的影响忽略不计［4］。③计算挠曲力时，不考虑伸缩力的影响［5］。④假设固定支座能完全阻止梁的位移，不计活动支座摩擦阻力的影响。用非线性有限单元法建立桥上道岔区道岔—轨道板—梁—墩一体化计算模型［6-8］，该模型中，道岔、轨道板、桥梁和墩台是一个相互作用、相互影响的耦合系统。图2(工况1)为简支梁桥1号墩固定计算模型，图3(工况2)为简支梁4号墩固定的计算模型。

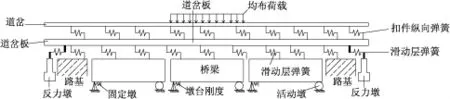
图2 工况1道岔—轨道板—梁—墩一体化计算模型

图3 工况2道岔—轨道板—梁—墩一体化计算模型

1.3 测点布置及测试内容

在本次模型试验中，钢轨应变是通过光纤光栅应变片来测得的，应变片布置见图4。位移通过百分表来测得，测点包括:①尖轨位移;②心轨位移;③尖轨附近限位器处基本轨、尖轨位移;④心轨附近限位器处基本轨、尖轨位移;⑤梁端位移(对于连续梁要测整个梁两端位移，对于简支梁要测每片梁两端位移);⑥墩位移;⑦梁、板相对位移;⑧固结机构、梁相对位移。

从梁体的右边开始用吊车向梁体吊装轨排荷载，吊装的顺序是从右到左，且一层一层地吊装。同时吊装过程中必须保证四层轨排摆放端正，不能出现偏心放置的情况。每吊装一块轨排，待轨排稳定地放置于钢支架上时，试验人员方可读取测点的读数，同时记录下读数的时刻，这样可以使仪器采集的数据与位移测点的记录数据同步，以方便数据的处理。挠曲力加载过程见图5。

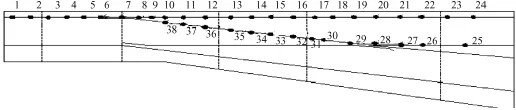
图4 光纤光栅应变片布置

图5 挠曲力加载过程

2 试验结果分析

2.1 挠曲力测试

基本轨挠曲力理论值的计算采用岔—板—梁—墩一体化计算模型。由无缝道岔的结构可知，在垂向荷载作用下，道岔的尖轨、心轨和里轨的挠曲力均较小，基本轨在固定区，有相对较为明显的挠曲力。因此，基本轨的挠曲力最具有代表性，以道岔区基本轨作为研究对象，分析道岔区挠曲力的分布机理。

根据图3所示的应变测点布置图，进行3次测试，测出各个测点的力。图中“+”表示钢轨受拉，“-”表示钢轨受压，坐标原点为桥梁左边第一墩。由图6和图7可以看出，由于施加在该模型结构上的轨排荷载较小，纵连板式无砟轨道结构试验测得的数据较小，只有在施加荷载的梁体部位测点有相对较为明显的位移数据，没有施加荷载的梁体部位测点的数据基本为0，即使有，可能都是因为人为原因造成轨道板的振动而导致百分表产生很小的位移数据。纵连板式无砟轨道的基本轨挠曲力最大为5 kN，最小挠曲力出现在2号梁体部分的基本轨区域，简支梁左边墩固定时基本轨产生的挠曲力与简支梁右边墩固定时基本轨产生的挠曲力基本相等。

2.2 位移测试

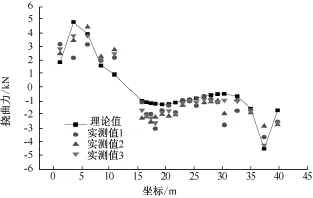
图6 简支梁纵连板1号墩固定基本轨挠曲力实测值与理论值对比

图7 简支梁纵连板4号墩固定基本轨挠曲力实测值与理论值对比

道岔、无砟轨道道床板及桥梁理论位移的计算仍采用岔—板—梁—墩一体化计算模型。根据各测点3次测出的位移值的平均值和理论计算得出表1的结果(工况1)，可以看出:纵连板简支梁1号墩固定试验中2号梁体处左边梁端的位移较大，位移达到0.313 mm;而右边梁端的位移较小，为0.004 mm，主要是因为2号梁体的梁面比较宽，受同样大小荷载作用时，其端部的位移值就比较小。其次桥上无缝道岔结构部分的变形也非常小，只有岔心以及尖轨部分有一定的位移量，其中尖轨尖端与轨道板的相对位移仅为0.009 mm，1号梁与3号梁处的位移测点基本没有位移。

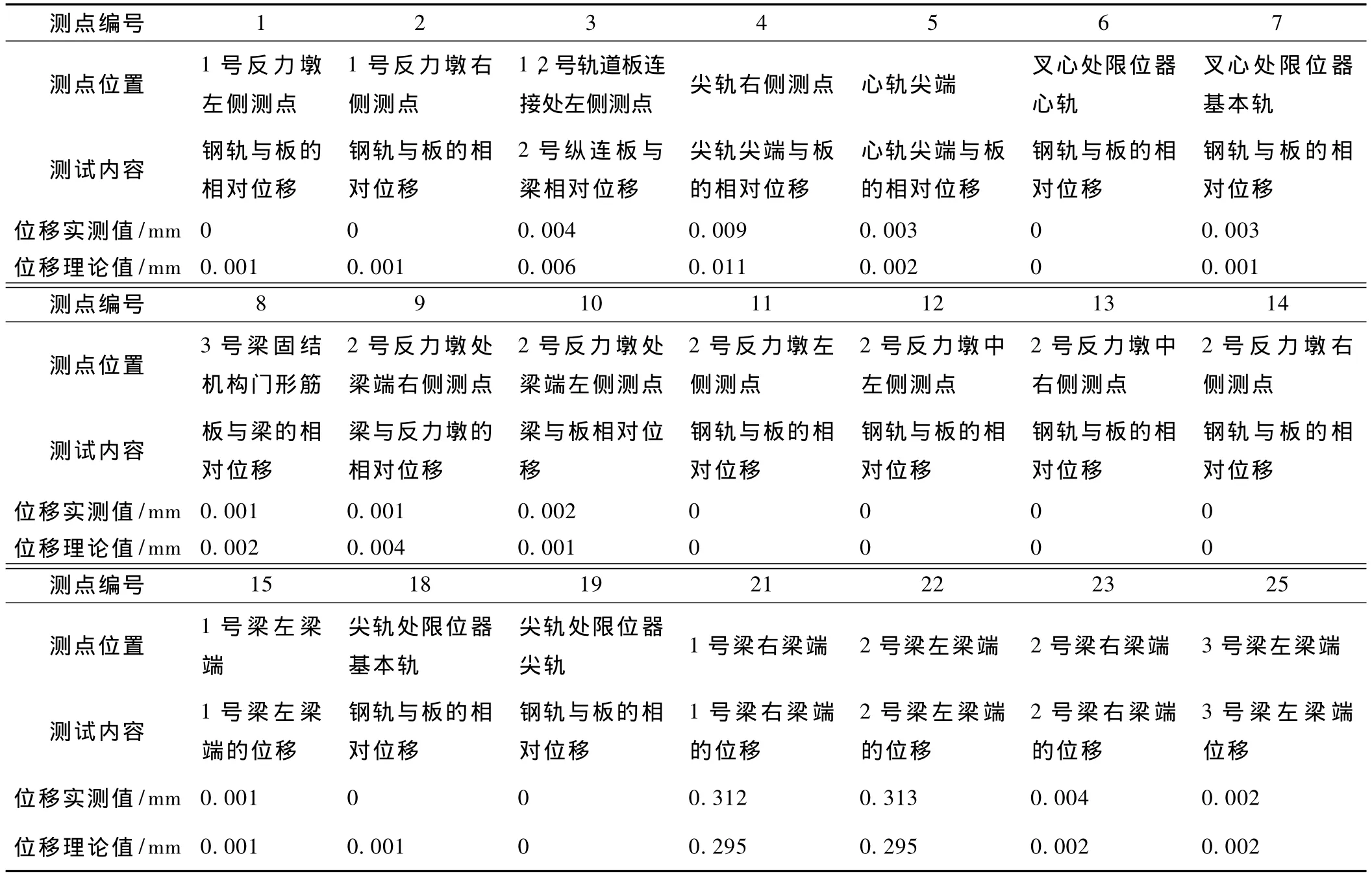
表1 纵连板简支梁1号墩固定的位移实测值与理论值对比

3 结论及建议

通过对该模型试验测试，得出简支梁桥纵连板在模拟挠曲力荷载作用下对桥上无缝道岔、轨道板、梁体结构的相互作用关系及其力和位移的变化规律。

1)简支梁固定支座布置位置对挠曲力有很大的影响。工况1中实测最大值为4 300 N，工况2中实测最大值为440 N;工况1中理论最大值为5 000 N，工况2中理论最大值为270 N。

2)当无缝道岔铺设在纵连板简支梁上时，道岔范围内并未出现最大挠曲力峰值，钢轨的最大挠曲力出现在道岔前端简支梁和路基的交界处，在桥梁和路基交界处将出现钢轨挠曲力的拐点。

3)桥梁刚度增大，挠曲力减小［9］。桥上无缝道岔梁的抗弯刚度比普通梁的抗弯刚度大，道岔梁在竖向荷载下的挠曲纵向位移较小，与文献［3］解释一致。

4)在桥上无缝道岔无砟轨道挠曲力的技术结果比较中，虽然理论计算值与测试值存在一定差异，但差值不大，在允许范围以内，且整体变化规律基本吻合。验证了非线性有限单元法建立桥上道岔—轨道板—梁—墩一体化计算模型的正确性。

［1］范俊杰，谷爱军，陈岳源.无缝道岔的理论与试验研究［J］.铁道学报，2000，22(2):55-59.

［2］卢祖文，杨应环.铁路无缝线路［M］.第四版.北京:中国铁道出版社，2005:224-225.

［3］王平，刘学毅.无缝道岔计算理论与设计方法［M］.第一版.成都:西南交通大学出版社，2007:240-245.

［4］任娟娟.桥上无缝道岔区纵连式无砟轨道受力特性与结构优化研究［D］.成都:西南交通大学博士学位论文，2009.

［5］卢耀荣，冯淑卿.桥上无缝线路挠曲力的计算［J］.铁道学报，1987(9):56-67.

［6］王平，杨荣山，刘学毅.无缝道岔铺设于长大连续梁桥上时的受力与变形分析［J］.交通运输工程与信息学报，2004，2(3):16-21.

［7］徐庆元.用有限元法分析无缝道岔的受力与变形［J］.中国铁道科学，2003，24(6):36-40.

［8］何华武.时速250 km级18号道岔设计理论与试验研究［J］.铁道学报，2007，29(1):66-71.

［9］刘棣华.高墩桥的桥梁和轨道相互作用的挠曲力［J］.中国铁道科学，1995，16(3):72-79.