岩体结构控制下的边坡稳定性多因素敏感性分析

李 扬，杨继红，刘汉东

(华北水利水电学院，郑州 450011)

水库边坡的稳定性研究对确保水利水电工程的建设及正常运营具有重要意义，其稳定性受诸多内外因素的影响［1］。在边坡稳定性评价中，敏感性分析是对影响边坡稳定性的因素进行检查和分析，确定影响边坡稳定性的最敏感或较敏感因素，从而使边坡监测更有针对性，使治理设计更安全、可靠和经济［2］。目前在边坡稳定性的敏感性分析中，广泛应用的是传统的单因素分析方法，但该方法存在明显的局限性。因需假定其中一个因素变化，而其它因素保持不变，而在实际中，单一因素发生变化的情况是很少的，故此假设往往与实际情况不符［3］。对此，笔者采用正交敏感性分析方法，对影响某水库工程边坡稳定性的控制性结构面——断层 F11与 F6，7，8的黏聚力和摩擦角(c、φ)进行敏感性分析及显著性检验，从而为该边坡的稳定性评价提供合理、可靠的依据。

1 边坡岩体参数正交试验

正交试验设计(Orthogonal experimental design)是研究多因素、多水平对象的一种设计方法。它是根据正交性，从全面试验中挑选出部分有代表性的点进行试验，这些有代表性的点具备了“整齐可比、均衡分散”的特点，因而是一种高效、快速、经济的试验设计方法，在很多领域的研究中已得到了广泛应用［4-5］。在边坡稳定性分析计算中，利用正交数值试验原理，设计参数的正交组合，进行边坡的稳定性计算，从而确定了设计参数对稳定性的影响大小。

1.1 边坡正交试验与设计水平

岩体边坡的稳定性主要取决于岩体的力学与变形特性。由于不同的岩体参数变异性有所不同，为了减小计算工作量，正交试验参数主要考虑变异性较大的岩体参数。本文将岩体黏聚力 c、内摩擦角 φ选作试验参数，并对每一参数选取三个值，即三个试验水平，用以研究岩体参数与边坡稳定性之间的关系。

1.2 正交试验稳定性分析

确定了试验变量和设计水平，就确定了相应的正交试验表。下一步建立边坡稳定性计算模型，也就是根据正交试验表中所确定每一次试验方案(即不同设计水平参数的组合)进行计算分析。四因素三水平的正交试验仅需进行9次数值分析，即可获得全部的正交试验分析结果。

2 龟头山岩体边坡稳定性影响因素分析

某水库，位于沁河中游太行山峡谷段的南端，以防洪为主，兼顾供水、发电等综合利用，是黄河下游防洪工程体系的主要组成部分。根据构造形迹，左坝肩的断层带和褶皱束既影响着龟头山体的稳定又可能引起水库的绕坝渗漏问题。其中，有两条断层起决定性作用:F11逆掩断层、F6，7，8断层带，见图 1。

2.1 结构面分级

岩体结构控制论认为岩体变形破坏主要受结构面控制，或者说岩体稳定性是受结构面控制的。按照谷德振［6］的观点，从规模上及其对岩体稳定性起的作用出发，可将结构面分为5级(见表1)。

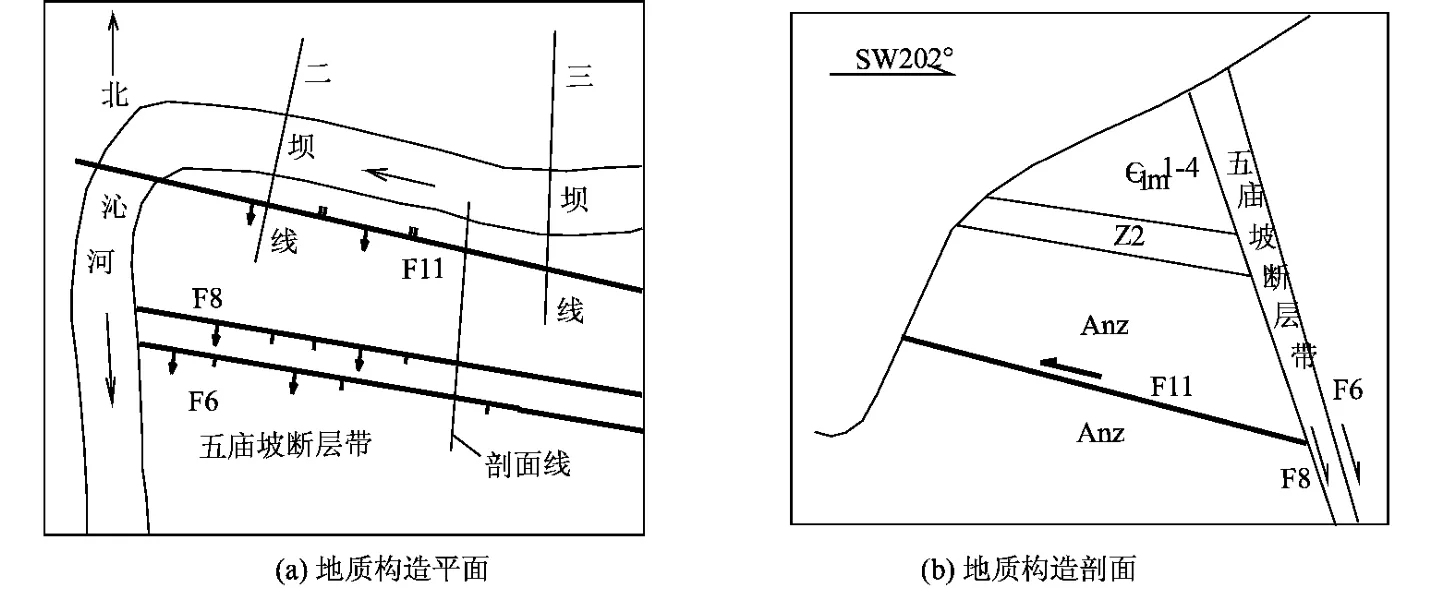
图1 龟头山地质构造示意

表1 结构面分级［6］

2.2 坝址区Ⅱ级结构面发育情况

根据表1中的结构面分级和岩体结构控制论的思想，对于坝址区山体或边坡岩体的稳定性，主要受控于Ⅱ级结构面:断层 F11和五庙坡断层带 F6，7，8。

F11逆掩断层走向 300°～310°，倾向 SW，倾角 15°～27°，最大倾角达51°。断层面呈舒缓波状，断距5～30 m。断层带宽度0.5～2.0 m，组成物质可分两个带，即断层泥带和压碎岩带。泥带厚1～10 cm，为含角砾的断层泥，遇水软化，分布不连续;压碎岩带厚0.4～1.9 m，为碎裂的片麻岩夹构造透镜体，挤压紧密。在垂向上，高程190～210 m以下，断层局部分成三个破裂面，倾角分别为 23°、20°、15°，以 23°为主断裂面。在断层两盘，往往发育有拖曳褶皱及羽状剪节理。

五庙坡断层带 F6，7，8(图 1)规模最大，对山体或边坡的稳定性起着控制作用而且分布在主体工程部位，与建库关系密切。五庙坡断层带主要由 F6、F7、F8三条近东西向的阶梯状正断层组成，断块北升南降。断层产状:F6走向 270°，倾向 S，倾角 50°～80°;F7走向270°～280°，倾向 S 或 SW，倾角 60°～87°;F8走向270°～280°，倾向 S或 SW，倾角45°～60°。断层走向、倾向稳定，但倾角在不同高程上变化较大，一般上陡下缓，破碎带在剖面上呈上宽下窄的楔形体。在破碎带中，除上述三条断层外，还发育两组次一级小断裂:一组是与主断层产状一致的高角度正断层;另一组是向北缓倾的俯冲式正断层，走向270°～300°，倾向 N或NW，倾角10°～30°。因此五庙坡断层带，是由很多断裂面与岩层层面错综交汇组合的破碎岩体。五庙坡断层带宽度6～70 m，带内各断层相距较近，破碎带互相联为一体，宽度大小受F6、F7、F8三条主断层在水平或垂直方向撒开或收敛所控制。破碎带组成物质为散体结构的断层泥、含泥角砾(泥和角砾带一般厚1.00～2.75 m)及碎块岩。

2.3 参数选取

根据可研报告提供的相关资料，可以确定龟头山边坡各层岩土体的初始计算参数如表2所示，F11与F6，7，8的抗剪强度参数设计水平取值如表3所示。

表2 龟头山各层岩土体初始计算参数表

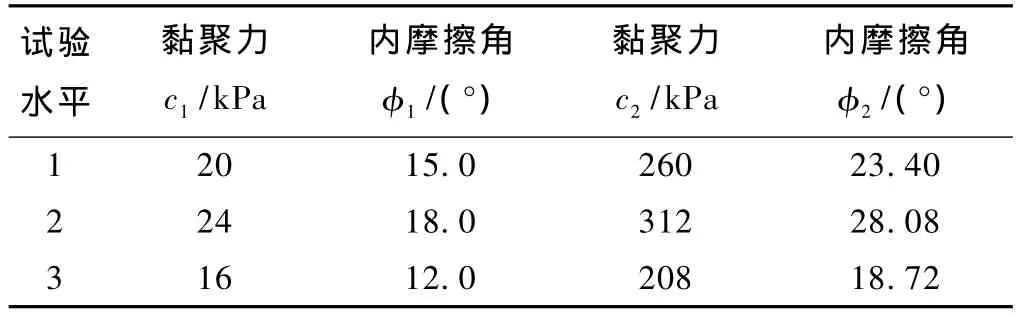
表3 F11与 F6，7，8的抗剪强度参数表

2.4 计算模型

稳定性分析选择刚体极限平衡法中的Morgensterprice法［7］，该方法有独特的优点，可用于评价各种类型边坡的稳定性，如圆弧滑动、非圆弧面滑动、平面滑动和楔形体滑动等复杂剖面的岩质边坡。Morgensterprice法有力学概念清晰、适用面广、操作简单的优点，与此同时能分析各种特殊结构对边坡稳定性的影响，且比较全面、客观地反映各种控制边坡稳定性因素的作用。采用软件Geoslope建立计算模型如图2所示。

图2 二坝线剖面二维极限平衡分析模型

2.5 计算结果与分析

按照四因素三水平正交试验表 L9(34)，断层 F11与断层带F6，7，8强度参数的正交试验结果及计算结果如表4所示。对表4中9个不同的组合进行稳定性计算，得到稳定安全系数Fs。将各个因素相同水平的试验结果求平均值，极差是在各水平的平均值中由最大值减去最小值求得。极差大说明此因子的不同水平产生差异较大，是重要因子。由表中极差Rj一行可知，断层F11的内摩擦角对边坡稳定性的影响最大，其次为断层带 F6，7，8的内摩擦角，断层带 F6，7，8的黏聚 力 与 断层F11黏聚力对边坡稳定性影响较小。各参数的敏感性排序为:φ1＞φ2＞c2＞c1。

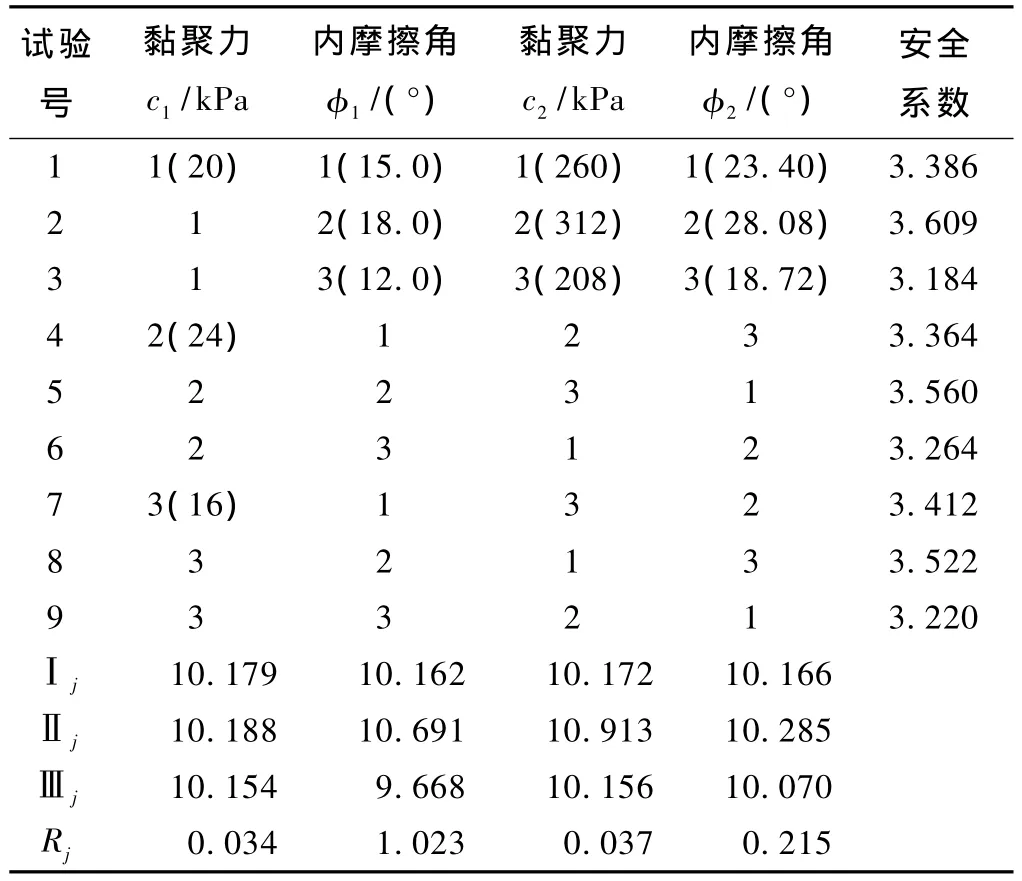
表4 F11与 F6，7，8的强度参数的正交试验结果

3 结论

根据坝址区主要Ⅱ级结构面的发育特征，通过地质分析表明对岩质边坡稳定性起控制作用的两个结构面是断层 F11和断层带 F6，7，8。基于正交试验设计理论和极限平衡方法，进行了边坡稳定性影响因素敏感性分析，得出断层F11的内摩擦角对边坡稳定性的影响最大，其次为断层带 F6，7，8的内摩擦角，而断层带 F6，7，8的黏聚力与断层F11的黏聚力对边坡稳定性影响较小。

［1］罗红明，唐辉明，胡斌.考虑地震力的刚体极限平衡法及其工程应用［J］.岩石力学与工程学报，2007，26(增 1):3590-3595.

［2］张万涛，余宏明.正交试验设计方法在库岸滑坡敏感性分析中的应用［J］.安全与环境工程，2009(5):13-16.

［3］王益萍，周荣超.基于正交试验的边坡稳定性参数敏感性分析［J］.盐城工学院学报(自然科学版)，2007(12):67-69.

［4］王恺忱，朱起茂，张止端.黄河流平衡纵剖面问题的探讨［C］//第二次河流泥沙国际学术讨论会论文集.北京:水利电力出版社，1983:620-627.

［5］贾绍凤，陆中臣.沿程淤积与溯源淤积的概念与数学模型［J］.地理学报，1992(2):157-164.

［6］李毓瑞，古迅，宋玉环.谷德振文集［M］.北京:地震出版社，1994:262-263.

［7］王四巍，刘海宁，刘汉东.黄河下游堤防边坡多因素敏感性分析［J］.人民黄河，2009(7):18-20.