地铁隧道施工引起地表沉降主要影响角的分析

韩 冬，苏三庆，郑选荣，温 静，张 海

(1.西安科技大学 建筑与土木工程学院，西安 710054;2.西安市地下铁道有限责任公司，西安 710054;3.中国中铁电气化局集团有限公司 西安分公司，西安 710054)

随着城市地铁隧道建设热潮的兴起，隧道施工引起的地表移动及变形问题在学术界和工程界都引起了广泛的关注。在对地层位移预测研究上，Peck法和随机介质理论法应用比较广泛。随机介质理论是波兰学者LITWINISYN［1］为研究采煤岩层与地表移动问题所提出的，经过我国学者刘宝琛、廖国华等［2］的发展和完善，已经和经典的Peck法成为我国在地层位移预测方面采用的主要理论方法。

很多文献指出，运用随机介质理论得到的地表沉降分布形态和由Peck法计算得到的结果相似，均符合高斯分布函数［4］。随机介质理论法来源于采矿工程，在我国被引入到城市地铁隧道施工引起的地表移动及变形研究还是近几年的事，因此在工程实践中还存在很多不明确的地方，特别是其关键参数的选取还没有成熟的方法。

因此，本文对Peck法和随机介质理论法进行了阐述，对这2种方法之间的关系进行了相关讨论，并给出了随机介质理论法主要影响角β的确定方法。

1 Peck法和随机介质理论法的基本原理

1.1 Peck法

PECK［5］在大量实测资料分析的基础上，于1969年在国际土力学大会上提出了地表沉降槽的横断面大致遵循正态分布曲线(又称高斯分布曲线)的规律。在此基础上，ATTEWELL 等人［6］和 RANKIN［7］总结了当时广泛应用的经验方法，并提出以下著名的计算地表沉降的Peck公式

式中，s为地面上任一点的沉降值;smax为地面沉降的最大值，位于沉降曲线的对称中心上(即隧道中心线的正上方)所发生的最大沉降;y为从沉降曲线中心到计算点的距离;i为从沉降曲线对称中心到曲线拐点的距离，一般称为“沉降槽宽度”。根据 O′REILLY和NEW［8］在伦敦地区的经验，i和隧道深度 z0之间存在以下简单的线性关系

式中，K为无量纲参数，称为沉降槽宽度系数，主要取决于土性，这一表达式目前在国际上被广泛接受。根据伦敦地区的经验，普遍认为，对于无黏性土此值在0.2～0.3之间;对于硬黏土，约为0.4～0.5;而对于软粉质黏土则可高达0.7。韩煊等人［9］建议西北地区均匀致密黄土取0.41。

定义地层损失率Vl为单位长度的地表沉降槽的体积占隧道开挖的名义面积A的百分比。D为隧道开挖直径，地层损失率Vl主要与工程地质条件、水位地质条件、隧道施工方法、施工技术水平以及工程管理经验等因素有关［10］。对于不排水条件，地层损失率 Vl与最大位移之间的关系可以通过对式(1)积分得到

把式(3)代人式(1)，可得

Peck法的提出使沉降的预测在数学计算上得到了大大简化。经过约40年的工程实践，已经积累了丰富的实际应用经验。目前，Peck法已经成为一个经典公式，很多其它的经验方法都是在这一方法的基础上进行修正得到的。

1.2 随机介质理论法

随机介质理论是波兰学者 LITWINISYN［1］为研究采煤岩层与地表移动问题所提出的。在经过我国学者刘宝琛、廖国华等的发展，其理论已逐步完善，已经广泛应用于矿山、隧道等工程的地表移动和变形预测［11-12］。该理论分析的对象是一种被称为“随机介质”的介质。由于常见的城市地铁隧道一般距离地表不深，大都处于表土或风化岩层中，这些介质能被较好地视为随机介质。从统计观点，可将整个隧道开挖看作无限多个无限小的开挖对上部地层影响的总和。如图1所示的一个开挖单元，在不排水、不固结、密度不变化的条件下，当开挖单元完全塌落时，上部地层的坐标点(x，y)的下沉w(x)(即为地表横向沉降槽)为

式中，r(z)为微单元开挖在深度为 z的水平面上的主要影响半径，也就是沉降槽的宽度。

图1 单元开挖空间坐标

根据荷兰学者 KNOTHE［13］提出的采矿工程中的经验，沉降槽的主要影响范围为

式中，β为隧道上部围岩的主要影响角。

根据上式定义，对于地表沉降槽(z=z0)，β的含义如图2所示。

图2 主要影响半径与影响角

实际上，任何地下隧道都不允许完全塌落，式(2)计算所得到的地表下沉为最不利的情况。隧道的施工过程中，常常对地层采取预处理和开挖后采取严密的支护措施，使得隧道建成后，隧道周围岩土体仅发生微小的位移。因此引起地表发生沉降的原因只是由于隧道周围岩土体向开挖空间运动而导致隧道开挖断面的收缩。如果隧道开挖初始断面为Ω，隧道建成后，开挖断面由Ω收缩为ω，如图3所示。则根据叠加原理，地表下沉应当等于开挖范围Ω引起的下沉与开挖范围ω引起的地表下沉之差，即

图3 隧道开挖示意

2 Peck法与随机介质理论法的关系

在式(4)中，AVl的物理意义为隧道开挖后的收敛面积(即隧道开挖断面面积的减小量)。假定开挖一微型隧道(用微元 dξdη表示)完全塌陷，则其收敛面积为 dξdη，代入式(4)可得

与式(5)比较，可以发现二者形式完全相同。因此，本文设

因此可知，对于一个足够小的开挖单元引起的地表变形，Peck法与随机介质理论法得到的沉降槽曲线分布趋势基本一致。Peck法可以看作是随机介质理论法在应用于埋深较大、开挖断面较小的隧道的一个近似，即z0/R(R为隧道开挖的当量半径)足够大的情况。而随机介质理论法得到的地表沉降曲线是一系列微小单元开挖引起的地表变形高斯曲线的叠加，与隧道开挖断面的几何性质有关。

综上所述，Peck法适用于埋深大、开挖半径小的隧道。而浅埋的大断面隧道，其引起的地表变形不可避免地受到开挖断面形状和隧道收敛具体情况的影响。由于随机介质理论法是直接基于隧道开挖断面收敛部分面积的积分，因此可以反应隧道断面形状和收敛情况的影响。

3 随机介质理论法主要影响角β的确定

随机介质理论是最近几年来从采矿工程引入到城市浅埋地铁隧道开挖引起的地表移动及变形研究计算当中得来的，因此对相关计算参数的基本规律和选用还缺乏一定经验。

在随机介质理论法中，主要影响角β控制沉降槽的计算宽度。

3.1 Knothe公式

将式(6)代入式(9)，可得

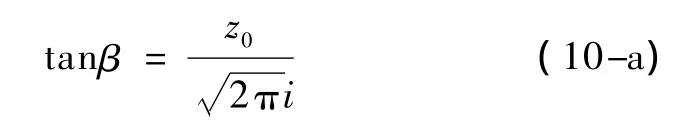
或

式(10)即为Peck法所得沉降槽宽度与随机介质理论法中主要影响角β的关系。

在随机介质理论法中，目前采用的 Knothe公式［13］为

式中，φ为地层土的内摩擦角。

对比式(10)和式(11)，可以得到主要影响角为

如果将常用的 i=0.5z0代入式(10-a)，可得 β=38.59°，则相当于 φ=12.81°。具有这样指标的土一般为软弱黏土。这与“伦敦硬黏土中一般K的均值为0.5左右”的理论明显不符。由此可见，按照此方法计算，得到的β值较小，最终计算所得的沉降槽过于平缓，影响范围扩大。

3.2 本文建议方法

β为隧道上部围岩的主要影响角，根据大量实测资料，β值并非式(6)中定义所得。本文定义β为沉降槽外缘至隧道外侧起拱点连线与水平线的夹角，R为主要影响半径。如图4所示。则式(6)修正为

图4 主要影响半径与影响角

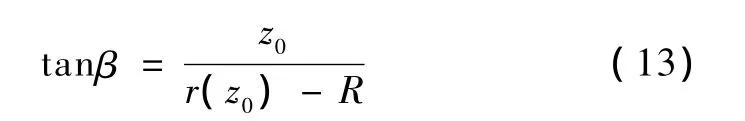
将式(2)、式(9)代入式(13)可得

4 算例分析

为验证本文建议方法的正确性，本文借用阳军生和刘宝琛［12］中采取的算例和西安地铁进行验证。

北京地铁复兴门由南向北两条正线和一条折返线所组成，采用浅埋暗挖新奥法施工。地铁结构处于第四纪冲积层中，主要由粉细砂及砂砾石组成。开挖工作在地下水位线以下，南正线隧道开挖跨度约为8 m，高度6.4 m。取横断面B(S)161+56进行分析讨论，此断面隧道拱顶距地表面11 m，如图5所示。地铁南正线开挖完成后地表下沉实测值如表1所示。

表1 B(S)161+56断面地表下沉实测值

图5 B(S)161+56断面示意(单位:m)

应用式(14)，K 取值为 0.38，tanβ≈1.496，取隧道开挖收敛值 ΔR=15.60 mm，获得相应的地表沉降曲线与实测值比较结果，如图6所示。

图6 计算结果与实测值比较

西安地铁北大街段由南北两条正线组成，采用盾构法施工。地铁结构处于第四纪冲积层中，主要由均质黄土组成。开挖工作在地下水位线以下，南正线隧道开挖跨度约为6.14 m，覆土厚度14.1 m，隧道开挖横断面如图7所示。地铁东正线开挖完成后地表下沉实测值如表2所示。

表2 断面地表下沉实测值

图7 断面示意(单位:m)

应用式(14)，K 取值为 0.41［9］，tanβ≈1.239，取ΔR=2.00 mm，获得相应的地表沉降曲线如图8所示。

图8 计算结果与实测值比较

5 结论

1)分析讨论了Peck法与随机介质理论法的关系。Peck法适用于埋深大、开挖半径小的隧道，可以看作是随机介质理论法在应用于埋深较大、开挖断面较小的隧道的一个近似。而浅埋的大断面隧道，其引起的地表变形受到隧道断面形状和收敛情况的影响，采用随机介质理论法可以得到较为准确的结果。

2)结合Peck法的研究成果，对随机介质理论法主要影响角β的确定方法进行了讨论，认为目前对主要影响角确定的公式不符合实际情况，会得到较为平缓的地表变形曲线。本文结合工程实际给出了β的确定公式，并验证该法基本符合工程实际情况。

［1］LITWINISYN J.The theories and model research of movements of ground［C］//Proc Eur Ground Movement，1957.

［2］刘宝琛，廖国华.煤矿地表移动的基本规律［M］.北京:中国工业出版社，1965.

［3］HUDSON JA.Comprehensive Rock Engineering［M ］.Newyoke:Pergamon Press，1993.

［4］刘波，陶龙光，叶圣国，等.地铁隧道施工引起地层变形的反分析预测系统［J］.中国矿业大学学报，2004，33(3):277-282.

［5］PECK R B.Deep excavations and tunnelling in soft ground［C］//Proceedings of the 7th International Conference on SMFE.Mexico City:［s.n.］，1969:225-290.

［6］ATTEWELL P B，YEATES J，SELBY A R.Movements Induced by Tunnelling and Their Effects on Pipelines and Structures［M］.Blaxkie:Glasgow，1986.

［7］RANKIN W J.Ground movementresulting from urban tunnelling:predictions and effects［C］//Proceedings of the 23rd Annual Conference of the Engineer Ground of the Geological Society Held at Nottingham University［s.l.］:Geological Society Publishing House，1988:79-92.

［8］O′REILLY M P，NEW B M.Settlements above tunnels in the United Kingdom-their magnitude and prediction［C］//Proc.Tunnelling 82，published by Institution of Mining and Metallurgy.London:［s.n.］，1982.173-181.

［9］韩煊，李宁，STANDING J R.Peck公式在我国隧道施工地面变形预测中的实用性分析［J］.岩土力学，2007，28(1):23-28.

［10］BURLAND J B，STANDING J R，JARDINE F M.Assessing the risk of building due to tunnelling-lessons from the Jubilee Line Extension，London［C］//Geotechnical Engineering:meeting society needs.Proc.of the Fourth Southeast Asian Geotechnical Conf.Hong Kong，2001:17-44.

［11］刘宝琛，张家生，廖国华.随机介质理论在矿业工程中的应用［M］.长沙:湖南科技出版社，2004.

［12］阳军生，刘宝琛.城市隧道施工引起的地表移动及变形［M］.北京:中国铁道出版社，2002.

［13］KNOTHE S.Observationsofsurface movementsunder influence of mining and their theoretical interpretation［C］//European Conf.on Ground Movement，1957:210-218.