四种方法测木质材料动弹性模量的对比研究

齐永峰，徐华东，王立海

(1.黑龙江省森林工程与环境研究所，哈尔滨150081;2.东北林业大学，哈尔滨150040)

弹性模量是木质材料力学性质的重要衡量指标之一。传统检测弹性模量的方法是静载荷法，这种方法是目前公认最准确的方法，但其检测繁琐费时，且对木质材料具有一定破环性，并不适宜于实际生产中的大规模检测，因此急需寻找快速、准确并且无损的方法来对木质材料的静弹性模量进行估计。目前，国内外学者对木质材料力学性质无损检测已经进行了较多的研究［1-6］，研究发现应力波、超声波以及声共振等方法在木质材料动弹性模量检测领域具有显著的优势和潜力。然而，同时利用多种手段对木质材料弹性模量进行检测并对不同方法进行比较的研究还相对较少。

本文利用纵向应力波、超声波、纵向共振以及弯曲共振等四种方法对无缺陷木质材料的动弹性模量进行检测，并与其静弹性模量进行对比分析，进一步探讨研究木质材料静、动弹性模量之间的关系以及不同检测方法的优越性等内容。

1 材料与方法

1.1 试验材料

选用色木进行研究，色木样本采自黑龙江省方正林业局。在加工厂，把色木样本加工成规格为420mm×20mm×20mm的试件，数量为41个。制好的试件在温度、湿度相对稳定的实验室内放置3个月，使其气干状态下的含水率达到相对稳定。

1.2 动弹性模量测试方法

1.2.1 纵向应力波法

采用匈牙利FAKOPP公司生产的Microsecond Timer对试件进行测试。首先，在试件一个端面的中心点钉入激励传感器，再在另一个端面钉入接收传感器。然后，用力锤轻轻敲击激励传感器，试件内部将会产生一个应力波。应力波信号被接收传感器获取后传递到Microsecond Timer计时器里面，应力波在试件内的传播时间将会被计算出来。因此，利用式 (1)就可以计算出纵向应力波测量的动弹性模量［7］。

式中:MOEsw为纵向应力波法测量的动弹性模量(GPa)，ρ为试件密度(kg/m3)，C为传播速度(m/s)，L为试件长度(m)，T为传播时间(s)。

1.2.2 超声波法

与应力波检测方法相似，采用“穿透法”测试，在试件的一端用发射换能器发射超声脉冲波，在试件的另一端由接收换能器接收超声波信号。为了尽量减小换能器与试件之间空气介质的影响，在二者之间涂抹黄油耦合剂。利用中国科学院武汉岩土力学研究所研制的型号为SY5的RSM超声仪分析信号并获取超声传播速度，进而采用(2)计算超声波测量的动弹性模量MOEul。

式中:MOEul为超声波法测量的动弹性模量(GPa);ρ为试件密度;C为超声波传播速度。

1.2.3 纵向共振法

试验设备为FAKOPP公司的Portable Lumber Grader(PLG)。首先，用支撑木块和天平把被测试件支撑起来，试件的重量信息将会记录在测重放大器中，进而被传送到计算机中参与计算。然后用小锤击打试件的一端产生振动信号，在另一端则用高灵敏度的麦克风采集振动信号并把它传送到PLG软件进行解析，得到试件的共振频率。最后，依据试件的重量、尺寸、共振频率及含水率计算色木的动弹性模量。式(3)为试件密度的计算方法，式(4)为PLG计算木质材料动弹性模量的表达式。

式中:MOEev为纵向共振法测量的动弹性模量(GPa);为试件密度;M为试件质量(kg);L为试件长度(m);w为试件宽度(m);h为试件高度(m);u为含水率(%);f为纵波振动频率。

1.2.4 弯曲共振法

试验仪器采用A＆D公司型号为AD-3651-02的FFT信号分析仪，激振器和接收传感器分别为DYTRAN公司型号5800B4的应力锤和型号3035B的加速度传感器。试验时先将试件用柔软的细绳悬挂起来，使其处于近似的“自由状态”，再用装有力传感器的应力锤敲击试件的端部或中部，另一端的加速度传感器将会感应到振动信号并把其传达到FFT信号分析仪，最后通过分析得到试件的共振频率。因此，可以利用式(5)计算弯曲共振法测量的动弹性模量［8］。

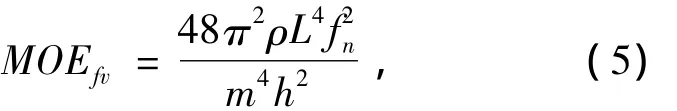
式中:MOEfv为弯曲共振法测量的动弹性模量(GPa);ρ为试件密度(kg/m3);L为试件长度(m);h为试件高度(m);fn为试件弯曲共振频率;n为振动频率的阶数;m为阶数决定系数(m=4.730，7.853，…)。

1.3 静弹性模量测试方法

采用珠海三思计量仪器公司生产的型号为CMT6305的万能力学试验机对所有试件进行静弹性模量测试。采用三点弯曲试验法，试件支撑点跨距l为360mm，上压头移动速度为2mm/min，试验过程中要注意试件弯曲量不能过大，以免压断试件。Bancheriau等［9］研究表明可以用式(6)计算试件的静弹性模量。

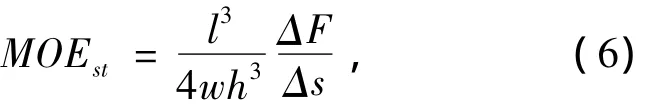
式中:MOEst为试件静弹性模量(GPa);l为支撑点间距离(mm);h为试件高度(mm);w为试件宽度(mm);ΔF为载荷—变形图中直线段载荷的增加量(kN);Δs为在力ΔF区间试件中点的垂直位移量(mm)。

2 结果与分析

2.1 试验结果

运用不同方法和设备测量41个试件的统计数据见表1。从表1可以看出，样本试件的密度平均值为969.26 kg·m-3，变异系数小于5%;绝干含水率平均值为10.04%(采用烘干法测量样本绝干重量并计算样本含水率)，变异系数也小于5%;这表明样本试件的基本物理性质比较稳定。表1还显示，运用四种方法得到的动弹性模量MOEdy均要高于静载荷方法测得的静弹性模量MOEst，造成这种差异的主要原因是不同测试方法所采用测试原理不尽相同，另外还因为木材是一种粘弹性材料，在静载荷测试时，木材的变形存在一定的“滞后”效应。

表1 试件的试验数据Tab.1 Experimental data of the specimens

2.2 静动弹性模量相关性分析

为分析木质材料静、动弹性模量之间的相关性，运用统计软件SPSS分别对四种方法测得的动弹性模量MOEdy与静弹性模量MOEst进行一元线性回归分析，结果如图1～4所示。图1～4表明，四种方法测得的动弹性模量 MOEdy与静弹性模量MOEst之间均具有比较显著的线性相关性。样本决定系数R均超过0.7，可以认定有较好的拟和度。

由于四种方法测得的动弹性模量MOEdy与静弹性模量MOEst之间的线性相关性均比较显著，因此运用这四种方法对木质材料的动弹性模量MOEdy进行检测，进而对木质材料的静弹性模量MOEst进行估计是可行的。

图1 MOEsw与MOEst的关系Fig.1 Relationship between MOEswand MOEst

图2 MOEev与 MOEst的关系Fig.2 Relationship between MOEevand MOEst

图3 MOEfv与 MOEst的关系Fig.3 Relationship between MOEfvand MOEst

图4 MOEul与 MOEst的关系Fig.4 Relationship between MOEuland MOEst

2.3 不同方法比较分析

以静载荷测试方法检测得到的静弹性模量MOEst为试件弹性模量的“真值”，讨论纵向应力波、超声波、纵向共振和弯曲共振等四种方法得到的动态弹性模量MOEdy与静弹性模量MOEst的差异，进而通过对比分析找出估计木质材料静弹性模量最为准确的方法。

采用配对t检验对四种方法检测得到的动弹性模量MOEdy与静弹性模量MOEst的差值平均值分别进行检验，检验结果见表2。配对t检验能够对同一组受试样本采用两种不同方法检测得到的结果进行差异性分析，其使用条件为:①被检验两组样本具有配对关系;②两组样本容量均大于或等于30，来自正态总体。而本次试验所得到的样本数据均满足上述要求。

从表2可以看出，MOEsw-MOEst、MOEev-MOEst、MOEfv-MOEst和 MOEul-MOEst的显著性概率均小于0.001，从而表明在置信度为95%时，四种方法检测得到的动弹性模量MOEdy与静弹性模量MOEst均具有显著性差异。图5是四种方法得到的样本试件动弹性模量与其静弹性模量的配对差值和相关程度比较图。从图5和表2可知，尽管四种方法得到的MOEdy与MOEst均有显著性差异，但差异程度并不一样，弯曲共振法得到的动弹性模量MOEfv与静弹性模量MOEst的差值均值最小，为1.629;超声波法的差值均值最大，为5.432。本研究中，MOEsw、MOEev、MOEfv和 MOEul比 MOEst分别高出26.3%、27.4%、11.5%和38.3%。这一结论与以往研究结论基本一致。殷亚方等［2］对加拿大云冷杉类大尺寸规格材检测表明，MOEev比MOEst高出5%～15%。Ilic［10］测得桉树小规格试件的 FFT分析MOEev值比静态弯曲试验所获得的MOEst高出29%。Smulski［11］以北美洲四种阔叶材为对象测得MOEsw值比MOEst高出22% ～32%。这些研究均表明，木质材料的动弹性模量要略高于其静弹性模量。

表2 试验数据配对t检验分析结果Tab.2 Analysis results of experimental data using t test

图5还比较了四种方法得到的MOEdy与MOEst之间的相关程度，其关系为＞＞＞。也就是说，弯曲共振法测得的动弹性模量MOEfv与静弹性模量MOEst的相关性最为显著，R2为0.9037;而纵向应力波测得的动弹性模量MOEsw与静弹性模量 MOEst的相关性最低，R2为0.7084，但也比较显著。这一结果与刘镇波等对大尺寸实木板材测试结果类似［12-13］，他们得出“MOEev与 MOEst的相关性弱于 MOEfv与 MOEst的相关性”的结论。另外，罗彬等［4］对小规格巨尾桉木材研究表明，与超声波和共振法相比，纵向应力波法得到的MOEsw与MOEst的相关性较低。

图5 静动弹性模量配对差值及相关程度比较Fig.5 Paired difference and relevance comparison between MOEdyand MOEst

上述分析表明，与其它三种方法相比，弯曲共振法得到的样本试件动弹性模量MOEfv与静弹性模量MOEst的差值均值最小，而相关性最高，因而运用弯曲共振法对木质材料静弹性模量进行估计最为准确，检测值也最接近静弹性模量值。

3 结论

(1)运用纵向应力波、超声波、纵向共振和弯曲共振法检测得到的木质材料动弹性模量均高于其静弹性模量。

(2)四种方法测得的动弹性模量与静弹性模量之间均呈比较显著的线性相关性，R2都大于0.7，因而都可以用来估计木质材料静弹性模量。

(3)与其它三种方法相比，弯曲共振法得到的样本试件动弹性模量MOEfv与静弹性模量MOEst的差值均值最小，而相关性最高，因而运用弯曲共振法对木质材料静弹性模量进行估计最为准确，检测值也最接近静弹性模量值。

［1］周海宾，任海青，费本华，等.木质复合板弯曲、剪切弹性模量动态测试［J］.建筑材料学报，2007，10(5):561 –565.

［2］殷亚方，吕建雄，倪 春，等.横向振动方法评估大尺寸规格材静态抗弯弹性性质［J］.北京林业大学学报，2005，27(5):107–110.

［3］韩 健.定向竹木复合板表观弹性模量预测模型的构建［J］.南京林业大学学报(自然科学版)，2009，33(1):33–36.

［4］罗 彬，殷亚方，姜笑梅，等.3种无损检测方法评估巨尾桉木材抗弯和抗压强度性质［J］.北京林业大学学报，2008，30(6):137–140.

［5］ Murata K，Kanazawa T.Determination of Young's modulus and shear modulus by means of deflection curves for wood beams obtained in static bending tests［J］.Holzforschung，2007，61(5):589–594.

［6］罗菊英，杨学春.结构用材应力波无损评价研究现状与展望［J］.森林工程，2009，25(6):31-36.

［7］ Wang X，Ross R，Eriskson J，et al.Nondestructive evaluation of standing trees with stress wave methods［C］.Proceedings of 12 International Symposiums on Nondestructive Testing of Wood.2000:197–206.

［8］ 李 坚.木材学［M］.北京:高等教育出版社，2002:256–258.

［9］ Bancheriau L，Bailleres H，Guitard D.Comparison between modulus of elasticity values calculated using 3 and 4 point bending tests on wooden samples［J］.Wood Science and Technology ，2002 ，36(3):367–383

［10］ Ilic J.Relationship among the dynamic and static elastic properties of air-dry Eucalyptus delegatensis R.Baker［J］.Holz als Roh-und Werkstoff，2001，59(3):169 –175.

［11］ Smulski S.Relationship of stress wave and static bending-determined properties of four northeastern hardwoods［J］.Wood and Fiber Science，1991，23(1):44–57.

［12］刘镇波，刘一星，于海鹏，等.实木板材的动态弹性模量检测［J］. 林业科学，2005，41(16):126–131.

［13］费本华，林利民，赵荣军.轻型木结构用规格材性能试验及钉连接承载性［J］.林业科技，2010，35(2):33-37.