DEM水平分辨率对流域特征提取的影响分析

鲍伟佳，程先富，陈旭东

（安徽师范大学 国土资源与旅游学院，安徽 芜湖241003）

数字高程模型（Digital Elevation Model，DEM）是地理信息系统地理数据库中最为重要的空间信息资料和赖以进行地形分析核心数据系统［1］。其中栅格DEM由于其结构简单、适合于计算机处理和存储等特征而被广泛应用于流域地形分析中。由DEM提取流域水文特征的关键步骤是确定单元格的水流流向，因而流向算法和DEM的分辨率是影响特征提取精度的主要因素。国内外学者在这些方面进行了大量的研究，刘学军［2］等通过对比汇水面积对目前流行的5种路径算法进行比较，得出D8［3］算法较之其他算法虽然计算精度较低，但由于其计算效率高并对地形有较强的适应能力［2］，而被普遍使用；吴险峰［4］、易卫华［5］等则在大、中型流域内分析了DEM分辨率对流域特征的影响，DEM的水平分辨率对提取河网的精确性有影响，网格的增大增加了平地处流向的随意性［4］，网格单元越小，提取结果越精确。而地形指数［6］自1979年由Beven等提出以来，已被广泛应用于水文模拟及集水区经营等相关研究［7］。解河海［8］等通过对比地形指数概率分布情况比较了单流向、多流向等算法的提取结果并提出了改进多流向算法。前人的研究大多集中在大、中型流域尺度上，且都拥有实测数据可以和流域特征提取结果进行对比，进而得出最适宜的DEM分辨率，在小流域尺度上且缺乏实测数据情况下的研究较少，所以通过对比不同分辨率DEM的流域特征提取结果和地形指数计算结果来选取适合的DEM分辨率是十分必要的。

1 数据和方法

1.1 研究区概况

本文选取杭埠河上源晓天河位于安徽省舒城县龙潭村的小流域作为研究区，流域面积7.9km2，海拔100～540m。研究区的地理位置及DEM见图1。该地区属亚热带温润性季风气候区，年平均气温15.6℃，年平均降雨量1 100mm，无霜期年平均224 d，四季分明，气候温和。

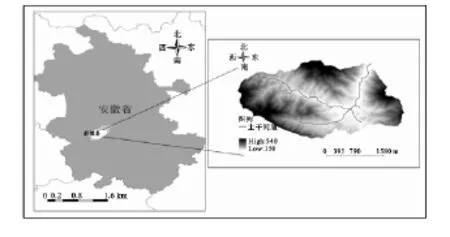
图1 研究区地理位置及DEM

1.2 基础数据

研究采用的原始数据是中国人民解放军总参谋部测绘局编绘的1984版的1∶1万纸质地形图。采用1954北京坐标系，1956黄海高程系，等高距为5 m。利用ArcView对扫描后的地形图等高线和高程点进行数字化，在ArcView空间分析模块下把等高线和高程点数据转换成TIN，再由TIN依次内插成水平分辨率为5，10，15，20，25，30，35，40，45，50m的栅格DEM。

1.3 流域特征提取方法

本文采用美国ESRI（Environmental Systems Research Institute）公司提供的ArcHydro Tools水文扩展模块提取流域特征。常用的基于DEM提取流域特征的软件还有RIVIX提供的River Tools、Garbrcht和 Martz的TOPAZ工具、美国Brigham Young大学环境模型研究实验室开发的WMS等。

使用ArcHydro Tools提取流域特征包括以下5个流程：DEM的预处理、水流流向的确定、汇流栅格的生成、自动生成河网、自流域边界的划分［9］。

DEM的预处理包括“burn－in”主干河网和填洼两部分，通过采用 Agree［10］方法“burn－in”主干河道来解决平坦地区的伪河道问题，并通过增加洼地高程值的方法进行填洼，使生成的河网连续。而在单元格流向确定方面则基于最陡坡面径流模拟方法，使用1984年由Mark等提出的D8单流向算法。该算法假设单元格中的水流只有8种可能的流向，即流入与值相邻的8个网格中。它用最陡坡度法来确定水流的方向，即在3×3的DEM格网上计算中心网格与各相邻网格间的距离权落差（即网格中心点落差除以网格中心点之间的距离），取距离权落差最大的网格为中心网格的流出网格，该方向即为中心网格的流向［11］。所有单元格流向确定后，便可计算出各单元格的上游汇流面积。河网则是通过设定最小集水面积阈值，集水面积大于等于该阈值则为河道这一方法自动生成的。设定的阈值越小，生成的河网越细密。最小集水面积阈值的大小应根据实际地形、气候等因素而确定，但由于缺乏实测资料，因此本文则是采用所有单元格汇流面积的平均值作为最小集水面积阈值，即为7 650m2。

1.4 地形指数计算方法

式中：TI——地形指数；α——单元长度等高线上游集水区（或特定的集水区）的面积；β——单元格的坡度。当前基于GIS的地形指数计算法则主要包括单流向算法（SFD），双流向算法（BFD）和多流向算法（MFD）。多流向算法则被普遍认为是其中最为精确的一种［12］。本文采用单流向算法即D8算法来计算地形指数。D8算法假定有效的等高线长度等于单元格长度，而坡度即为顺坡方向的最大坡度。因此D8算法的地形指数的表达式如式（2）。

式中：A——单元格上游集水面积；L——单元格长度；Δh——相邻栅格的最大高程差；Δl——具有最大高程差的两个相邻栅格单元的中心距离。

2 流域特征参数分析

将5～50m分辨率的10套DEM数据导入Arc－GIS并使用ArcHydro Tools模块进行计算分析。通过DEM 预处理（DEM Reconditioning）、填洼（Fill Sinks）、确定水流流向（Flow Direction）、上游集水面积计算（Flow Accumulation）、生成河网矩阵（Stream Definition）、河网分级（Stream Segmentation）、划分集水区（Catchment Grid Delineation）等步骤，定义最小集水面积阈值统一为7 650m2，并给定相同位置的流域出水口便可以计算出流域面积、河道总长度、最长河道等流域特征值，再使用ArcGIS软件中的空间分析功能可以计算出最长河道平均坡度和流域平均坡度等流域特征值。计算的流域特征值如表1所示。

表1 不同DEM分辨率流域特征参数表

从表1可以看出，栅格DEM的分辨率对计算所得的数字流域面积影响不大，流域面积最大值和最小值的差仅为平均值的0.62%，流域面积值随DEM栅格尺寸的增大总体呈平缓下降趋势，20m分辨率和40m分辨率DEM处有局部回升。造成流域面积变化的主要原因是随着DEM分辨率的下降，流域边界地区的栅格高程值被概化，致使所确定得边界地区栅格水流流向不同，且具有不确定性。

在河道长度方面，计算得出的河道总长度随着DEM分辨率的下降而急剧减小，其最小值仅为最大值的32.93%，而提取出的最长河道长度则变化平缓且呈无规律性，平均值为5 648.37m，最大偏差为293.11m，偏差幅度为5.19%（如图2所示）。虽然在提取河网时所采用的最小集水面积阈值统一为1 030m2，但受D8法限制，格网大小的变化会导致格网流向的变化，河道起始点的空间位置也会发生相应的改变，引起河流长度的变化［5］。加之由于DEM栅格尺寸越小，所提取的河道分级越细密，河道数目增加，从而使得河道总长度有明显增幅。而提取出的最长河道变化表现出无规律性也同样是由分辨率的变化会导致单元格流向的变化，从而使得最长河道起点的空间位置不同所造成。

由于DEM分辨率对流域面积的影响不大，而河网密度是河道总长度和流域面积的比值，因此河网密度的变化规律与河道总长度的变化规律极为相似。河网密度是反映流域河网发育程度的重要参数，河网密度越高说明流域河网发育越完全。从图3可看出，河网密度随DEM分辨率的升高呈减小趋势，且在15 m分辨率后变化趋于平缓。孔凡哲等人研究了集水面积阈值与河网密度的变化关系并指出：当集水面积阈值增大时，坡地网链逐渐移走；当增大到一临界值时，坡地网链全部从河网中移出［13］。在集水面积阈值不变、DEM分辨率为变量时，河网密度变化规律亦可作相同解释。

图2 河道总长度与最长河道长度变化情况

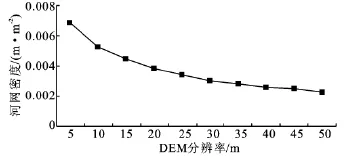
图3 河网密度变化情况

最长河道平均坡度即河道纵比降，为最长河道栅格单元高程值的平均变化率。随DEM分辨率变化情况由图4所示，除在10m分辨率DEM处有较强降幅外，其余分辨率DEM所提取的最长河道平均坡度皆变化不大，平均变化率为6.21%，且具有很大的随意性。从图5中可看出随着DEM分辨率的降低，流域平均坡度缓慢下降，平均降幅为2.72%。造成平均坡度变化的原因是由于栅格尺寸增大对单元格高程值有概化作用，降低了地形的复杂度，而导致最长河道平均坡度变化的主要原因是被概化后的栅格单元流向判别发生改变，从而使得最长河道起点空间位置不同。

3 地形指数分布特征分析

将由5～50m分辨率DEM提取的上游集水面积栅格图和坡度图分别进行栅格计算得出10幅地形指数空间分布图，并统计其最大值、最小值、平均值、标准差等特征值，如表2所示。

图4 最长河道平均坡度变化情况

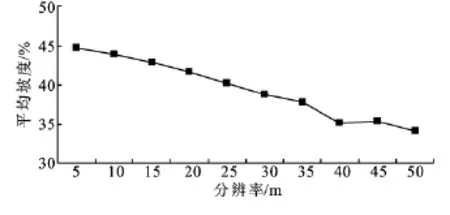
图5 平均坡度变化情况

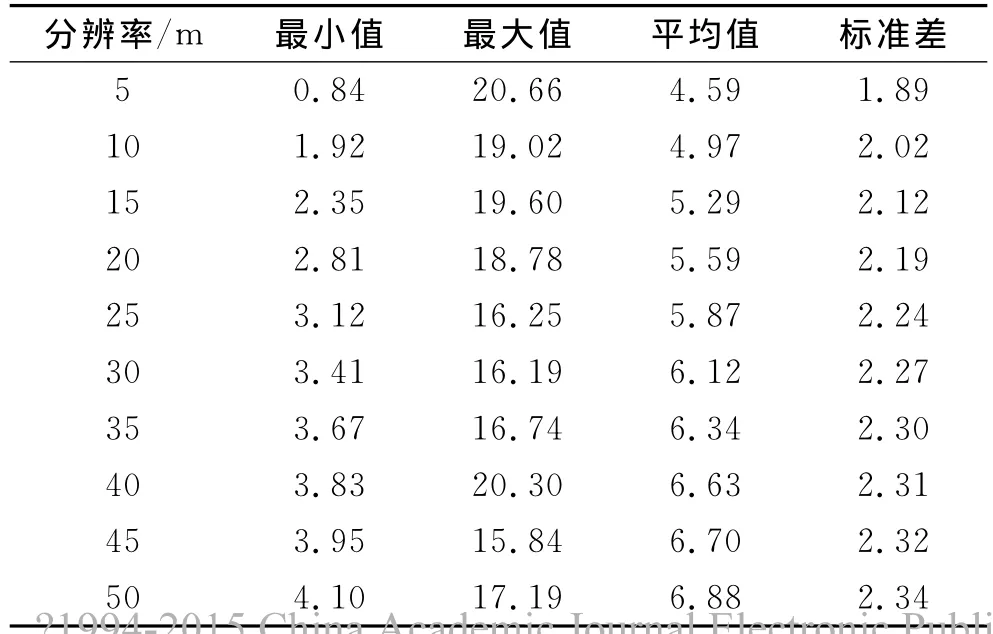
表2 不同DEM分辨率地形指数特征值

由表2可以看出提取的地形指数随DEM栅格尺寸的增大，地形指数最小值、平均值和标准差均增大，而最大值整体呈减小趋势。通过地形指数的表达式ln（α／tanβ）可以看出：地形指数最小值应分布在地形变化复杂的地区，而最大值应分布在地形平缓地势较低的流域出水口地区。在地形变化复杂的地区，降低DEM分辨率所产生的高程值概化作用较强烈，地形变化程度有所降低，坡度减小，是地形指数最小值增大的主要原因；而最大值的变化规律则难以解释。地形指数的平均值随DEM分辨率降低而增大的主要原因也同样是高程值概化作用。标准差的增大说明DEM分辨率越低则地形指数值分布越为离散。

由于地形指数的物理意义明确，即具有相同地形指数的点对将于具有相同的水文相应，而具有相同地形指数概率分布的流域具有水文相似性［14－15］，因此研究由不同分辨率DEM提取的地形指数概率分布具有很重要的意义。

分别统计5～10m分辨率DEM的地形指数概率分布，得出图6。

图6 不同DEM分辨率地形指数概率分布

由图6可看出，10套地形指数生成的概率分布图均为单峰状，5m分辨率DEM地形指数概率曲线最为平滑均匀，随着栅格尺寸的增大，分布图高值部分逐渐增多，曲线呈右偏趋势。5，10，15m分辨率DEM所提取的地形指数概率分布曲线形状极为相似，因而可以推断这3种分辨率的DEM能够反映相似的水文特征。

4 结论

（1）通过对比不同分辨率DEM提取的流域特征参数值可以看出，在本研究区内DEM分辨率越高，提取的河网越细密，而对流域面积、平均坡度等特征影响不大。

（2）DEM分辨率对流域特征提取结果的影响主要体现在栅格单元高程值的概化作用，在地形复杂的地区该作用表现的更为突出。

（3）在分析河网密度时发现，由15m分辨率DEM所得出的河网密度值趋于稳定，提取的河网中坡度网链被移除，消除了由更高分辨率DEM提取的河网冗余；而在分析地形指数概率分布时发现，5，10，15m这3种分辨率的DEM能够反映相似的水文特性，因而可以判定15m分辨率为本研究区域较合理的DEM分辨率。

［1］ 汤国安，赵牡丹，曹菡.DEM地形描述误差空间结构分析［J］.西北大学学报：自然科学版，2000，30（4）：349－352.

［2］ 刘学军，卢华兴，卞璐.基于DEM的河网提取算法的比较［J］.水利学报，2006，37（9）：1134－1141.

［3］ Callaghan F，Mark D M.The extraction of drainage networks from digital elevation data［J］.Computer Vision，Graphics and Image Processing，1984，28：323－344.

［4］ 吴险峰，刘昌明，王中根.栅格DEM的水平分辨率对流域特征的影响分析［J］.自然资源学报，2003，18（2）：148－154.

［5］ 易卫华，张建明，匡永生.水平分辨率对DEM流域特征提取的影响［J］.地理与地理信息科学，2007，23（2）：34－38.

［6］ Quinn P F，Beven K J，Lamb R.The ln（α／tanβ）index：how to calulate it and how to use it within the TOP－MODEL framework［J］.Hydeological Processes，1995，9：161－182.

［7］ 庄永忠，廖学诚，詹进发.不同网格解析度与流向演算法对莲华池集水区地形指标之影响［J］.地理学报（台湾），2007，（50）：73－100.

［8］ 解河海，黄国如.地形指数若干计算方法探讨［J］.河海大学学报：自然科学版，2006，34（1）：46－50.

［9］ 唐从国，刘丛强.基于Arc Hydro Tools的流域特征自动提取：以贵州省内乌江流域为例［J］.地球与环境，2006，34（3）：30－37.

［10］ Hellweger F.AGREE－DEM Surface Reconditioning System［DB／OL］.http：／／www.ce.utexas.edu／prof／maidment／ferdi／ferdi／research／agree，1996.

［11］ 李丽，郝振纯.基于DEM的流域特征提取综述［J］.地球科学进展，2003，18（2）：251－256.

［12］ Bin Yong，Wan Changzhang，Guo Yueniu.Spatial statistical properties and scale transform analyses on the topographic index derived from DEMs in China［J］.Computers ＆ Geosciences，2009（35）：592－602.

［13］ 孔凡哲，李莉莉.利用DEM提取河网时集水面积阈值的确定［J］.水电能源科学，2005，23（4）：65－67.

［14］ Beven K J，Kirkby N J.A physically based variable contributing area model of basin hydrology［J］.Hydrological Sciences Bulletin，1979，24（1）：43－69.

［15］ 邓慧平，李秀彬.地形指数的物理意义分析［J］.地理科学进展，2002，21（2）：103－110.