船舶纵向下水新工艺研究
2011-05-07李安慰
李 安 慰
(沪东(中华)造船集团有限公司,上海 200129)
1 纵向船台下水的技术现状及问题
船舶的下水方式通常有:船坞下水、纵向船台下水(可分为滚珠下水和牛油下水)、横向船台下水、浮船坞下水、气囊下水、起吊下水。当前最为普遍采用的下水方式是船坞下水和纵向船台下水。纵向船台下水通常易发生的危险情形有:艉跌落(艉弯)、艏跌落、滑道支撑受损、船体结构受损、船艏碰撞船台基面、船台侧壁碰撞、滑行冲撞障碍物[1]。在潮位过低时,避免艉跌落、艏跌落尤为艰难。
近年来,纵向船台下水的计算方法有了很大发展。在传统采用的静力学方法进行计算和分析的基础上,杜忠仁认为下水时船体是变刚度弹性基础上的变断面梁,通过计算得出了支墩反力沿着船长的纵向分布[2];顾永宁基于有限元法提出了纵向下水的弹性计算方法,并通过有限元模型计算一系列滑行位置时船体梁的垂线受力平衡和变形协调,得出每一个支墩反力,从而确定船舶结构内力,对下水全过程进行强度分析[3];卢镇光等按照船体弹性梁思想,提出了弹性船体的支座反力计算方法,对下水时支座反力进行分析计算[4];马骏等运用有限元法结合实船总体强度的计算结果,构造船体的三维模型,对下水时船底局部强度进行了分析和计算[5]。由静力学分析到弹性分析,再到全面的有限元法的应用,使得下水计算越来越精确和合理了。
如何避免艏跌落或艉跌落?一般采取的措施有:设置压载调整重心位置、改变船体基线坡度、向水下延伸滑道、选择高潮位日下水[1]。
2 纵向船台下水的风险分析及设置浮箱的理论基础
由于船舶艉部线性较艏部丰满,因此船舶下水时一般采取尾部先入水的方式。如果重心滑过滑道末端之前艉部还没有浮起,当重心滑过滑道末端之后如果发生浮力对滑道末端力矩小于重力对滑道末端力矩,将发生艉跌落。如果艉跌落得以避免,当艏部滑至滑道末端时船舶还没有全部浮起(亦即艏部没有浮起),将会发生艏跌落。
为避免艏跌落或艉跌落,可以采取压载调整重心位置。有时候,这样的调整可以避免危险的发生。但当潮位低到一定程度时,无论怎样调整重心位置,至少有一种危险情形——艏跌落或艉跌落将难以避免。
假设船台布置如图1所示,E为滑道末端点,A为初始位置时的船尾端点(艉垂线),C为初始位置时的船重心位置,F为艏垂线位置,P为初始位置时的托架首端点,Q为初始位置时的托架尾端点。

图1 船台布置
不发生艉跌落的条件是:当假定船舶沿滑道下滑(基线在艏艉位置与船台的间距保持不变)时,始终有
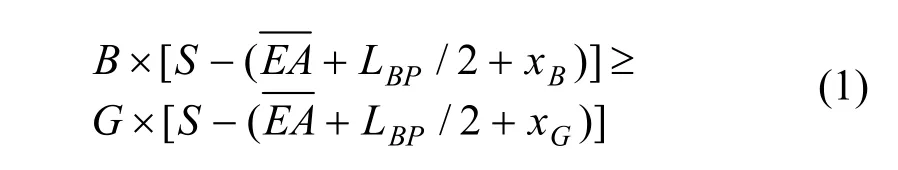
其中:S≥EA+LBP/2+xG;S——从初始位置到计算时刻的滑程;LBP——垂线间长(对应图1中的长度); xB——以船舯为原点时浮心位置纵向坐标; xG——以船舯为原点时重心位置纵向坐标;B——计浮力;G——计重力。
当式(1)不能成立时,将发生艉跌落。为保持式(1)成立,从理论上分析,可以增大B、或减小 xB、或减小G、或增大 xG,或兼而有之;减小G意味着要减少船上的安装项目。增大 xG意即重心向船艏移动,则必须在艏部加压载重量,使所需要的艏部吃水增加,这样在潮位不足时将导致另一种危险——艏跌落。能使得 xB减小的措施是增加基线斜度,但收效不明显。在一定滑程S时,浮力B=ρ∇g ,其中ρ为水密度,g为重力加速度,∇为排水体积。显然,水密度ρ及重力加速度g是难以改变的,要增加浮力,需增加排水体积∇。潮位升高显然可以增加确定滑程时的排水体积,向水下延伸滑道等于是增加了潮位,也可以增加排水体积。此外,给船体加设浮箱。
艏跌落不发生的条件是,自由浮态时托架首端点P处的吃水 TFP小于滑道末端有效水深H,即
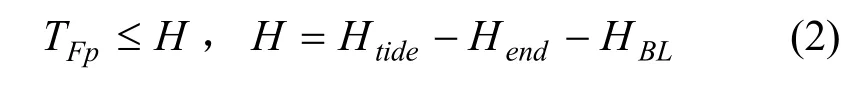
其中:Htide——潮位高度;Hend——滑道末端标高;HBL——船体基线BL到滑道面的距离。
与此等效的判别条件是:船舶到达滑道末端之时或之前( S≤ SF, SF——托架首端点到滑道末端的距离,即图1中),发生事故——浮力B等于重力G,即

当艏跌落发生时,如果艉部压载已经加到无以复加的程度,在艏部加设浮箱可以增加抬艏力矩从而减小艏部吃水,或者说可以有效增加浮力,使得浮力B大于重力G。
3 浮箱下水方案计算实例及浮箱位置的分析
现以某2万t货船为例,对加设浮箱的方案加以分析。计算时基础数据如下:
船舶两柱间长BPL : 155.79m
艉柱到滑道末端距离:60m
托架尾端点坐标:9.2m(以艉垂线为原点)
托架首端点坐标: 152.7m(以艉垂线为原点)
船体基线到滑道面距离BLH :0.55m
船台斜度:1/18
潮位高度tideH :2.2m
滑道末端标高endH :0m
下水重量 9400t(其中包含艉部压载600t)
重心坐标:(-5.895,0,10.75)(以船舯为原点)
下水区水密度ρ 1.02t/m3
3.1 未设置浮箱
采用邦戎曲线逐步计算间隔为0.5m滑程时的浮力及相关力矩,计算结果如图2所示。计算过程中,当艉浮发生后,假定几个不同纵倾值,以浮力对托架首端点的力矩达到与浮力对托架首端点的力矩相平衡为目标条件,逐步逼近平衡条件, 可以求出每一个计算滑程时的浮力及艏艉吃水。
图2中,M Gfp表示重力对托架首端点的力矩,MBfp表示浮力对托架首端点的力矩,M Gwe表示重力对滑道末端的力矩, MBwe表示浮力对滑道末端的力矩,G为重力,B为浮力。力和力矩均不考虑重力加速度因子,单位取为t和tm。 SF表示托架首端点滑过滑道末端时的滑程,定义为全滑程,即SF=,见图1。
滑程S=40.5m时,船体开始接触水面(对应图中原点位置),浮力产生,B曲线开始上升;滑程S=132m时,重心滑过滑道末端,此时 MGwe= 0;滑程S=156.5m时,M Bfp曲线上升至与 MGfp曲线等高度处,船舶艉部开始浮起;滑程S在132~156.5m之间时, MBwe曲线始终位于 MGwe曲线的上方,船舶不会发生艉跌落;滑程S=SF=60+152.7=212.7m时,托架首端点滑过滑道的末端。由图可以看出,此时,重力仍然大于浮力(曲线B始终位于曲线G之下),这表明船舶将发生艏跌落。
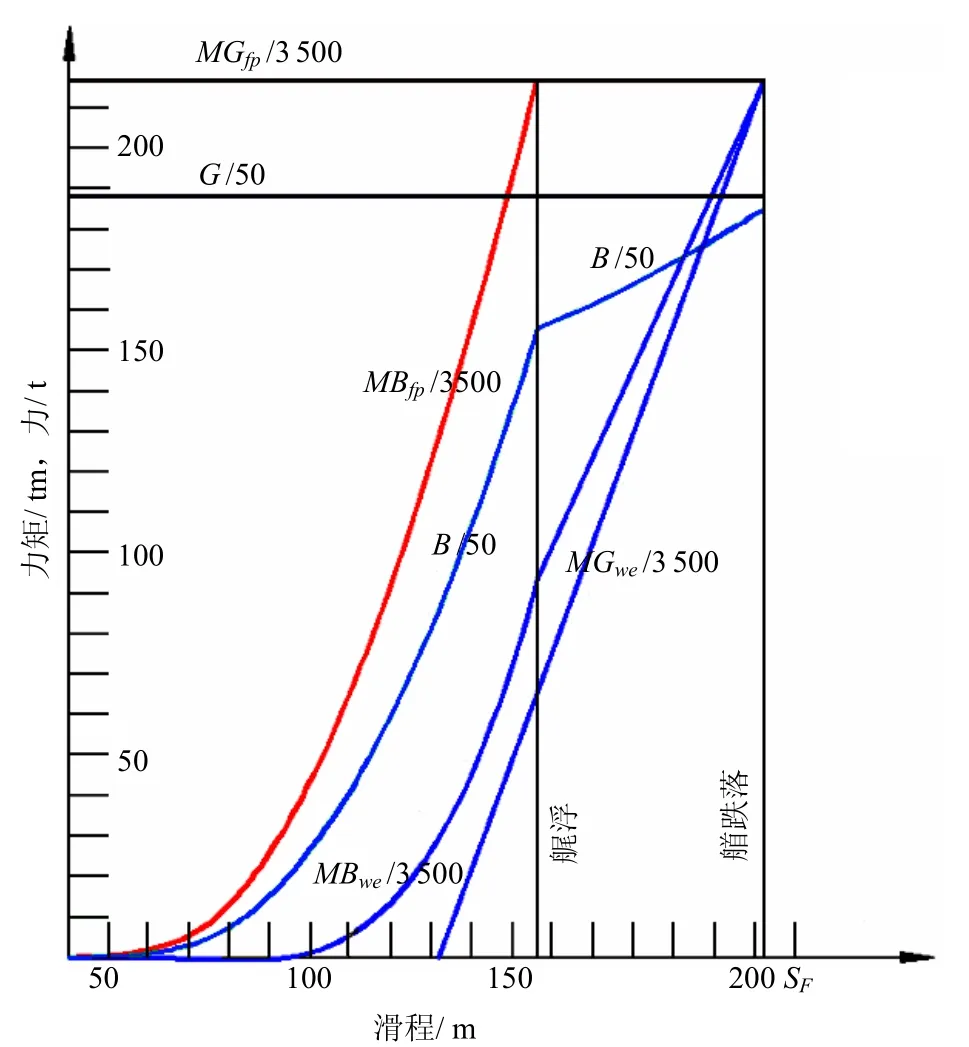
图2 未设置浮箱时计算的浮力和力矩
在此方案中,艉部已布置压载600t,继续在艉部加液体或固体压载受到局部强度及布置空间的制约。另外,艉浮发生在重心滑过滑道末端之后24.5m,继续在艉部加压载将导致艉跌落。而且为避免对滑道末端产生过大的压力,一般希望艉浮发生在重心滑过滑道末端之前或之后不多的区域。考虑到重量重心计算上的误差,继续在艉部加压载会导致艉跌落的风险急剧上升。
3.2 设置浮箱
浮箱左右对称布置。浮箱与托架紧固连接,并通过托架将浮力传递到船体。浮箱位置的确定需考虑:浮箱应尽可能小,以减少工装成本,并应保证必要的安全裕度。
在本算例中,危险情形为艏跌落,因此增加的浮力应当位于船体舯部至船体艏部的位置。为使浮力尽可能产生最大的抬艏力矩,浮箱的纵向位置宜尽可能向艏端移动。但增加的浮力效用必须发生在托架首端点滑过滑道末端之前,因此浮箱的纵向位置应位于托架首端点之后。浮箱的高度必须低于加浮箱后全浮时的水线。考虑到重量重心计算误差,全浮时的滑程应当小于托架首端点滑过滑道末端时的滑程(全滑程),并留有一定裕度,本算例中取目标裕度为全浮滑程小于全滑程5~6m。
为论证上述分析,假设浮箱中心位置分别位于X=X1=LBP/2,X=X3=SF-LBOX/2,X=X2=(X1+X3)/2三个不同位置(X值以船体艉垂线为原点),其中 LBOX为浮箱长度。取浮箱尺寸为:长 LBOX=28m,宽 BBOX=6m,高 HBOX=1.2m,左右舷各一个,对称布置。
1)浮箱 X=X1时,计算结果如图3所示。可以看出,当托架首端点滑过滑道末端时,重力G仍然大于浮力B,但浮箱的设置减小了二者的差值,起到了一定作用,但还是没能解决艏跌落的问题。

图3 浮箱X=X1时的计算结果
2)浮箱 X=X2时,计算结果如图4所示。当S=210m时,B曲线上升至与G曲线平齐,船舶开始全浮,此时托架首端点离滑道末端尚有SF-210=2.7m,艏跌落得以避免,并略有裕度。
3)浮箱 X=X3时,计算结果如图5所示。当滑程S=207m时,B曲线上升至与G曲线平齐,船舶开始全浮。此时托架首端点离滑道末端尚有SF-207=5.7m,艏跌落得以避免,并留有足够的裕度。

图4 浮箱X=X2时的计算结果

图5 浮箱X=X3时的计算结果
比较在不同位置设置浮箱的3个方案,可以看出,随着浮箱向艏部移动,艏跌落危险得以减小或避免,安全裕度加大。
当艉跌落发生时,首先可以考虑在艏部加压载措施。当艏部压载无以复加时,与上述分析类似,可以考虑在艉部设置浮箱,按照与艏跌落时加设浮箱同样的分析方法可以证明当浮箱位置靠近艉部时其体积最小。
4 结 语
按照上述分析,设置浮箱以解决艏跌落或艉跌落问题时,有以下几点结论及建议:
1)存在艉跌落危险时,首先考虑在艏部加压载,至无以复加为止,仍然不能避免艉跌落时才考虑设置浮箱。浮箱靠近艉部时体积最小。
2)存在艏跌落危险时,首先考虑在艉部加压载,至无以复加为止,仍然不能避免艏跌落时才考虑设置浮箱。浮箱靠近托架首端点时体积最小。
3)浮箱的设置应避免产生新的下水风险。如船台墙体间距紧张时,近舯部设置浮箱将增加船台侧壁碰撞的风险。艉部浮箱过大会导致艉浮过早从而导致艏部区域某些局部支反力超过船台或船体结构的承受能力,将导致船艏碰撞船台基面。
4)为使浮箱尽可能小,浮箱的高度不应超出加浮箱后的船体自由浮态时的水线。
浮箱的大小可以按照近似计算方法予以初步确定。艏跌落发生时,假设重力与浮力的差值为ΔB ,此时托架首端点处艏部吃水与自由浮态时的艏吃水的差额为ΔT,船台斜度角为β,需留取滑程裕度为6m,则浮箱的体积∇BOX应满足:
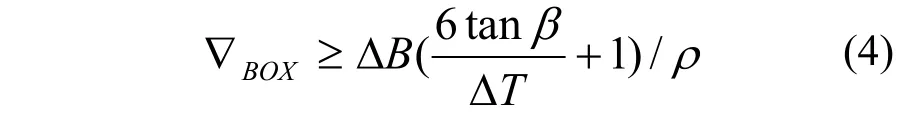
艉跌落发生时,假设滑出滑道1m时对滑道末端的浮力矩与重力矩的差额为MΔ,则增加的浮箱体积BOX∇应满足:

这是假定浮箱中心位置位于托架首端点处或艉垂线处得出的结论,实际计算时可先按照此公式给出的体积试算,然后对浮箱大小位置进行调整。
[1] 盛振邦,杨尚荣,陈雪深.船舶静力学(修订本)[M].北京:国防工业出版社,1984.
[2] 杜忠仁.船舶下水时船底部结构受损分析实例[J].造船技术,1992, (2): 27-32.
[3] 顾永宁.船舶纵向下水弹性计算方法和结构安全性[J].上海交通大学学报,1996, (10): 106-112.
[4] 卢镇光,束长庚.船舶纵向下水试验及支座反力的计算[J].中国造船,1996, (1): 53-58.
[5] 马 骏,邢金有,熊家敏.船舶下水底部局部强度分析[J].造船技术,1998, (5): 3-5.
