基于ANSYS的压电四维力传感器一种优化设计方法*
2011-05-06许斌,秦岚,薛联,刘俊
许 斌,秦 岚,薛 联,刘 俊
(重庆大学光电工程学院,重庆 400044)
一直以来,人类社会不断致力于改变信息摄取落后的现状,传感器技术成为迅猛发展起来的高新技术之一,它与通信技术、计算机技术构成了信息技术的三大支柱[1]。压电式多维力传感器在测量级别达到 106N的重机械以及测量微弱力信号的造纸技术等领域有着广泛而重要的应用[2-3]。目前传感器主要是根据设计者经验的被动设计,针对使用特点和应用场合的主动设计和优化设计还很难做到。传感器的优化设计最根本的问题是建立传感器数学模型,由数学模型揭示传感器弹性体的应力和应变关系,诠释传感器的力学特点和维间耦合的本质关系[4]。有限元的方法运用到传感器设计过程当中,如进行 PZT压电薄膜微传感器压电分析[5],压电式四臂加速度计模拟分析[6-7]以及三维力压电式加速度传感器设计[8]等,有效的解决了数学模型的建立和求解。在传感器结构中,内外环弹性膜主要用于调节传感器内外壁的刚度,使石英晶片均匀受力,减小传感器的微间干扰。但是由于弹性膜刚度小、受结构的影响大,对传感器灵敏度及刚度的影响就十分明显,同时内外环弹性膜本身精准数学模型建立及求解十分困难。文献显示,目前很少有弹性膜与传感器性能的关系的研究。本文运用 ANSYS有限元分析软件研究压电式四维力传感器灵敏度、固有频率与传感器内、外环弹性膜的关系,通过分析比较合理选取内、外环弹性膜参数,实现了传感器的一种优化设计方法。
1 传感器机理
压电式四维力传感器主要是通过不同切型的石英晶片按照特定的排列组合方式构成石英晶组进行空间力/力矩信息解析[9]。如图 1所示,晶片布局呈内、外双环结构。内环由八片 X切型晶片组成,用于测量空间 Z向力 Fz,晶片 Y轴(机械轴)径向发散,以减少维间干扰。外环由八片 Y切型晶片组成:其中两片的 X轴(电轴)与 X向平行,测量与传感器表面向切的 X向力 Fx;另外两片的 X轴与 Y向平行,测量 Y向力 Fy;剩下四片的 X轴与外环圆相切,并沿圆周方向等分排列[10],实现 X向力矩 Mx的测量。
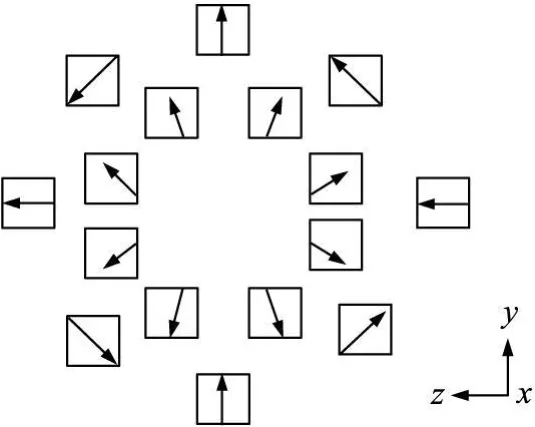
图1 传感器晶片布局
2 传感器有限元模型
2.1 传感器结构
传感器结构如图 2所示。由 1传感器外环弹性膜、2传感器内环弹性膜、3传感器内壁、4传感器上盖、5传感器外壁、6石英晶组、7传感器基座组成[11]。
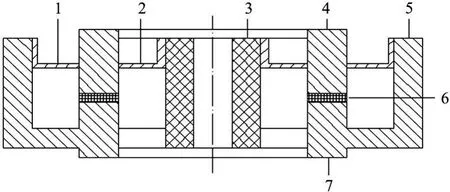
图2 传感器结构
载荷自传感器上盖分别通过传感器上盖,内、外环弹性膜,石英晶片传递到基座。
2.2 传感器有限元模型
如图 3所示:传感器有限元模型由 1预紧螺钉、2预紧上盖、3传感器、4工作台组成。图 3左边的为传感器晶片的布局图。
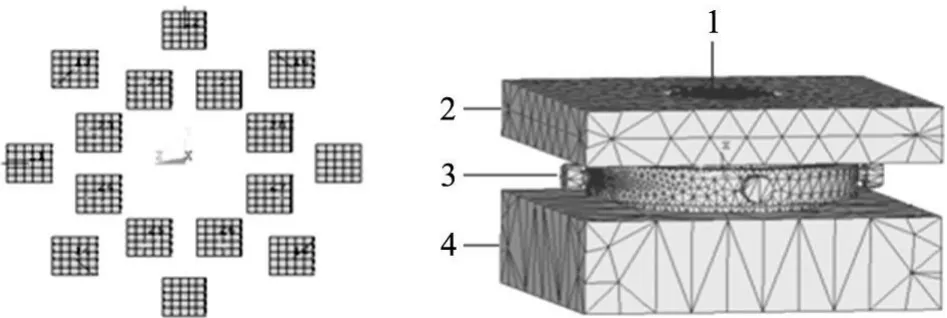
图3 传感器有限元模型
传感器结构参数如表 1所示。
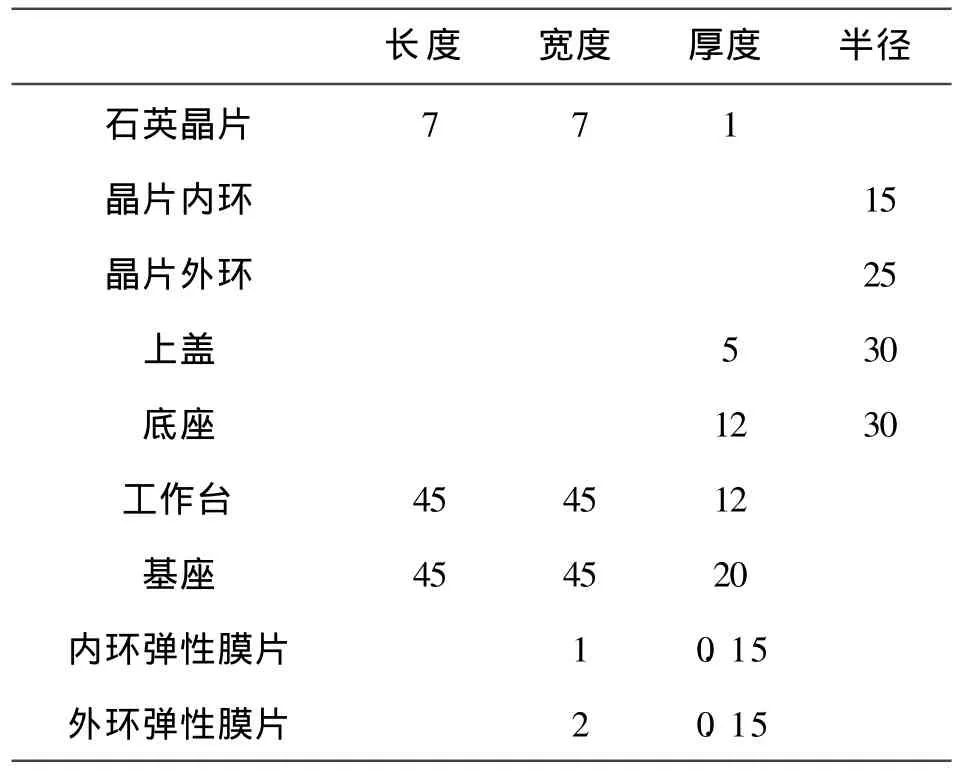
表1 传感器模型的结构参数(单位:mm)
在 ANSYS前处理器中建立传感器几何模型,并且按照传感器结构进行相应的布尔运算。为晶片分配耦合单元 SOLID5,为壳体和基座分配耦合单位SOLID98。建立壳体、基座、晶片的材料属性,按照各实体模型的各自的空间坐标系进行材料属性的分配。采用映射方式划分网格。进行相应的边界条件的设定:如晶片等势面的设定,基座空间自由度的设定,晶片与壳体连接面、壳体与基座连接面的设定。
3 优化设计
对于压电式四维力传感器来说其主要结构由底座、上盖和晶片组构成。在上盖和底座之间有一个弹性环节——弹性膜片的存在。为了达到提高灵敏度的要求,就应该使传感器的实际灵敏度尽量接近晶组的灵敏度。为了得到尽可能高的转换效率,那么弹性膜片的设计必须使作用在晶组上的载荷尽量大,消耗在外壳及弹性膜片的载荷尽量小,同时保证传感器的具有较高的固有频率。
所以在优化分析过程中,将内、外环弹性膜片的宽度及其弹性模量作为设计变量,传感器的灵敏度和固有频率作为目标函数,石英晶片的极限强度作为状态变量。由此通过数次循环仿真及结果分析研究内、外环弹性膜片的参数对传感器灵敏度和固有频率的影响。
采用 ANSYS的参数化设计语言的方法进行优化设计,其主要分析过程如图 4所示[12]。在设计优化循环文件时,须完成在前处理器 PREP7中建立参数化模型、在求解器 SOLUTION中求解、在后处理器POST/POST26中提取并指定状态变量和目标函数三个方面工作。
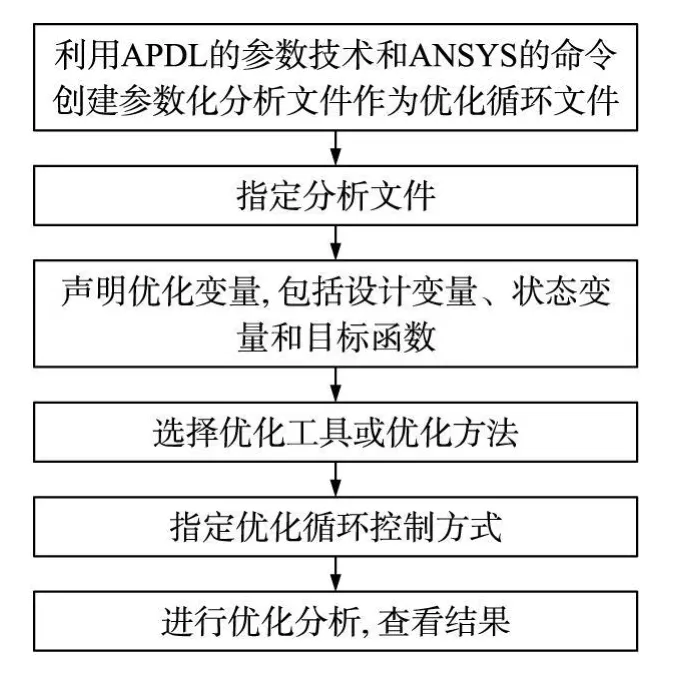
图4 优化设计流程
3.1 以传感器的灵敏度为目标函数
3.1.1 以弹性膜片的宽度为设计变量
在弹性膜片的弹性模量一定的情况下,研究弹性膜片宽度对灵敏度的影响。弹性膜片的厚度大约为 0.15 mm[10]。设计变量:L1-内环弹性膜的宽度(1 mm≦ L1≦ 6 mm);L2-外环弹性膜的宽度(2mm≦L2≦ 12 mm)。状态变量:SMAX-石英晶片的极限强度(SMAX≦ 1 e 8 Pa)。目标函数:UFY方向的电压。ANSYS中的优化分析是以目标函数最小作为最终目标,而在 FY方向施加正方向的外力时产生的电压是负值,这与施力方向和晶片的灵敏轴方向有关。所以实际设置的目标函数是 V=1 000+U,这样才能使输出电压的大小|U|(绝对值)最大。
在弹性模量取 2 e 9 Pa环境下得到输出电压与内环弹性膜片宽度的关系如图 5所示,与外环弹性膜的关系如图 6所示。
从图 5与图 6中可以看出:输出电压值随着弹性膜片宽度的减小而减小,但变换的范围并不是很大(电压变化随宽度变化的范围大约为45 V到35 V或 31 V到 27 V),也就是说,弹性模量为定值时弹性膜的宽度变化对输出电压的影响不是很大。
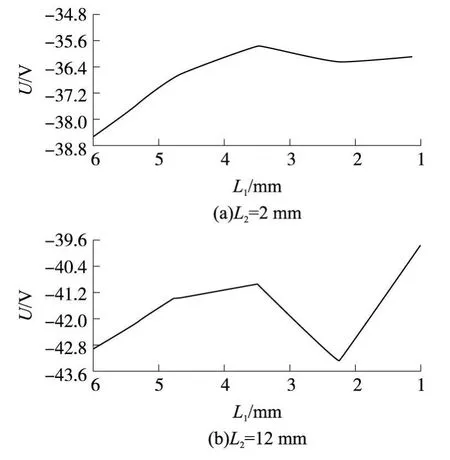
图5 内环弹性膜片L1与输出电压的关系
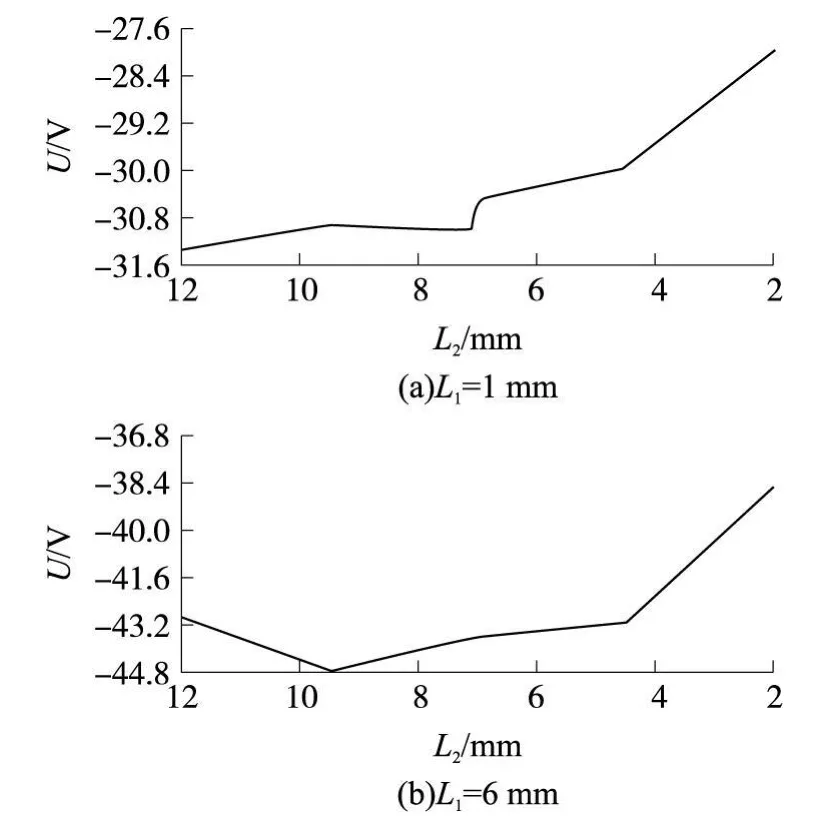
图6 外环弹性膜片L2与输出电压的关系
(2)以弹性膜片的弹性模量为设计变量
在弹性膜片尺寸一定,即弹性膜片厚度取0.15 mm,内、外环宽度也一定,极大值和极小值各取一次进行优化分析,得到弹性膜片的弹性模量与输出电压之间的关系。设计变量为弹性膜片的弹性模量 EX,2 e 7 Pa≤EX≤2 e 11 Pa,状态变量仍然为晶片的极限强度 SMAX,SMAX≦ 1 e 8 Pa,目标函数仍然为输出电压 U。得到输出电压和弹性模量之间的关系曲线,见图 7。
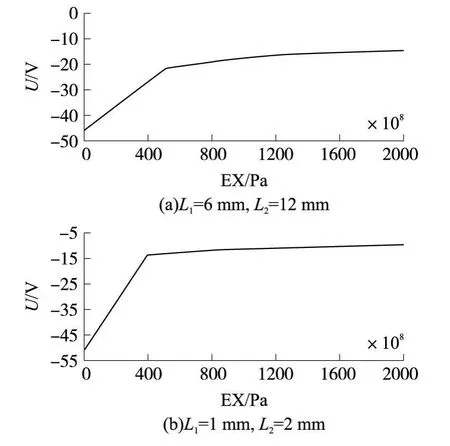
图7 弹性模量 EX和输出电压的关系
从分析结果表明随着弹性模量的增大,输出电压先迅速减小而后缓慢减小,。可见弹性模量对传感器的灵敏度有重要影响,改变弹性膜片的宽度,以及改变弹性膜片本身的弹性模量都会对传感器的输出有所影响。就其实质来说,改变上述参数,也就是改变了弹性膜片的刚度,当弹性模量减小以及宽度增大的时候代表刚度减小。而弹性膜片的刚度减小,根据力的分配比等于刚度的比,消耗在弹性膜片上的载荷就越小,传感器中晶片上受到的载荷就越大,因此传感器的灵敏度增大,与仿真结果一致。
3.2 以传感器的固有频率为目标函数
(1)以弹性膜片的宽度为设计变量
在弹性膜片的弹性模量一定时,研究弹性膜片的宽度对固有频率的影响。内环弹性膜片的宽度L1,外环弹性膜片的宽度 L2作为设计变量,石英晶片的极限强度 SMAX作为状态变量,传感器的一阶固有频率 F作为目标函数。这里实际取的目标函数是 10 000-F,原因是目标函数是以最小值作为优化目标,这样才能使传感器的一阶固有频率取最大值。
当 EX=2 e 9 Pa时,L1与固有频率的关系如图 8所示。
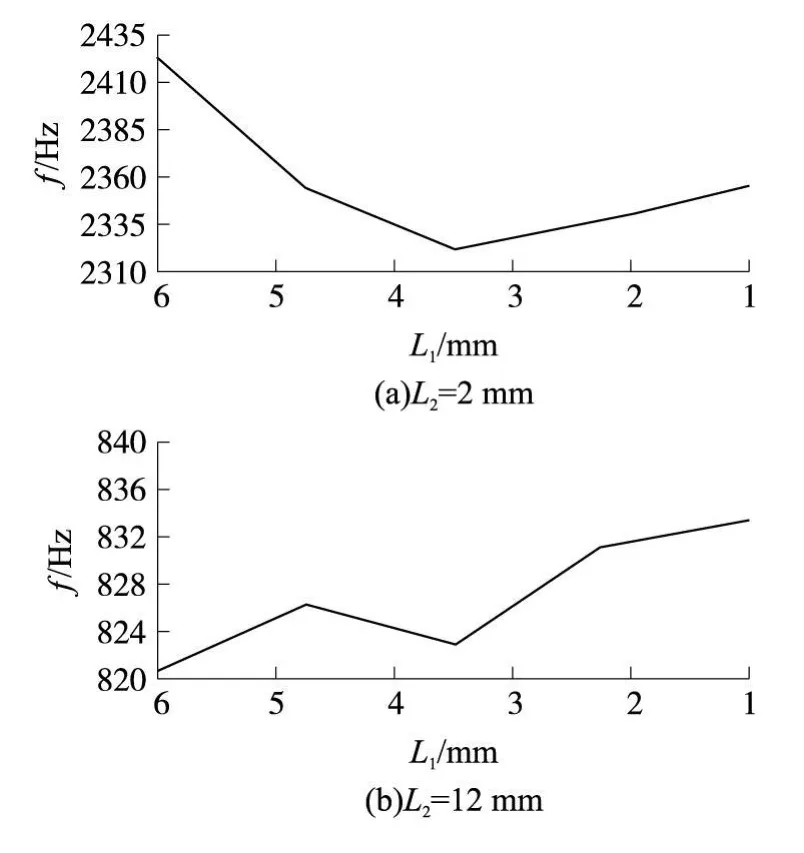
图8 内环弹性膜片宽度 L1与固有频率的关系
图8表明:弹性模量为定值时,弹性膜片的宽度与固有频率的关系:内环弹性膜片的宽度 L1的变化对固有频率影响不大:EX=2 e 9 Pa,L2=2 mm时,固有频率随内环弹性膜片宽度 L1变化而变化的范围是 2 325Hz到 2 425Hz;当 L2=12mm时,固有频率随内环弹性膜片宽度 L1变化而变化的范围是820Hz到 835 Hz。
L2与固有频率的关系如图 9所示。图 9表明:外环弹性膜片宽度 L2的变化对固有频率的影响较大:EX=2 e 9 Pa,L1=1mm时,固有频率随着外环弹性膜片宽度 L2变化而变化的范围是800 Hz到2 380 Hz;L1=6 mm时,固有频率随外环弹性膜片宽度 L2变化而变化的范围是 800 Hz到2 400 Hz。
(2)以弹性膜片的弹性模量为设计变量
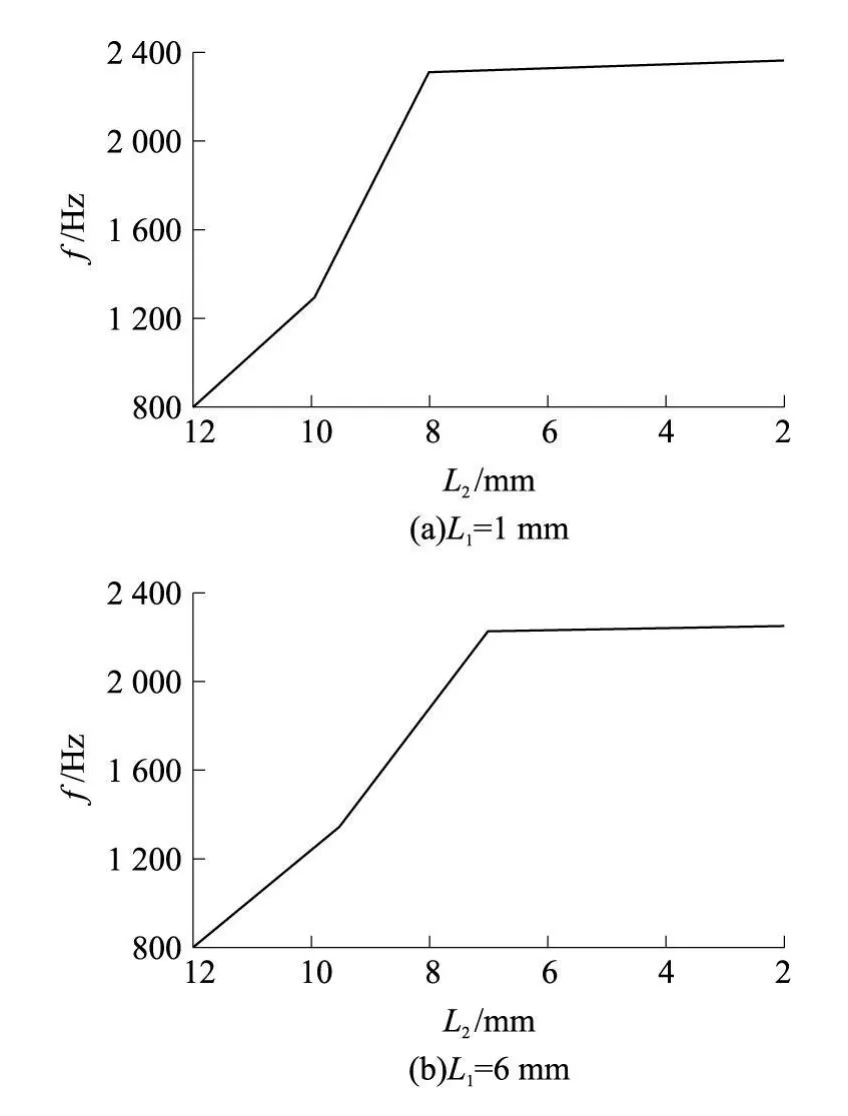
图9 外环弹性膜片宽度 L2与固有频率的关系
在弹性膜片宽度、厚度一定的情况下,研究弹性模量与固有频率的关系。设计变量为弹性膜片的弹性模量,2 e 7 Pa≦ EX≦ 2 e 11 Pa。分别取 L1=1mm,L2=2mm以及 L1=6mm,L2=12mm,得到弹性模量和固有频率的关系,见图 10。
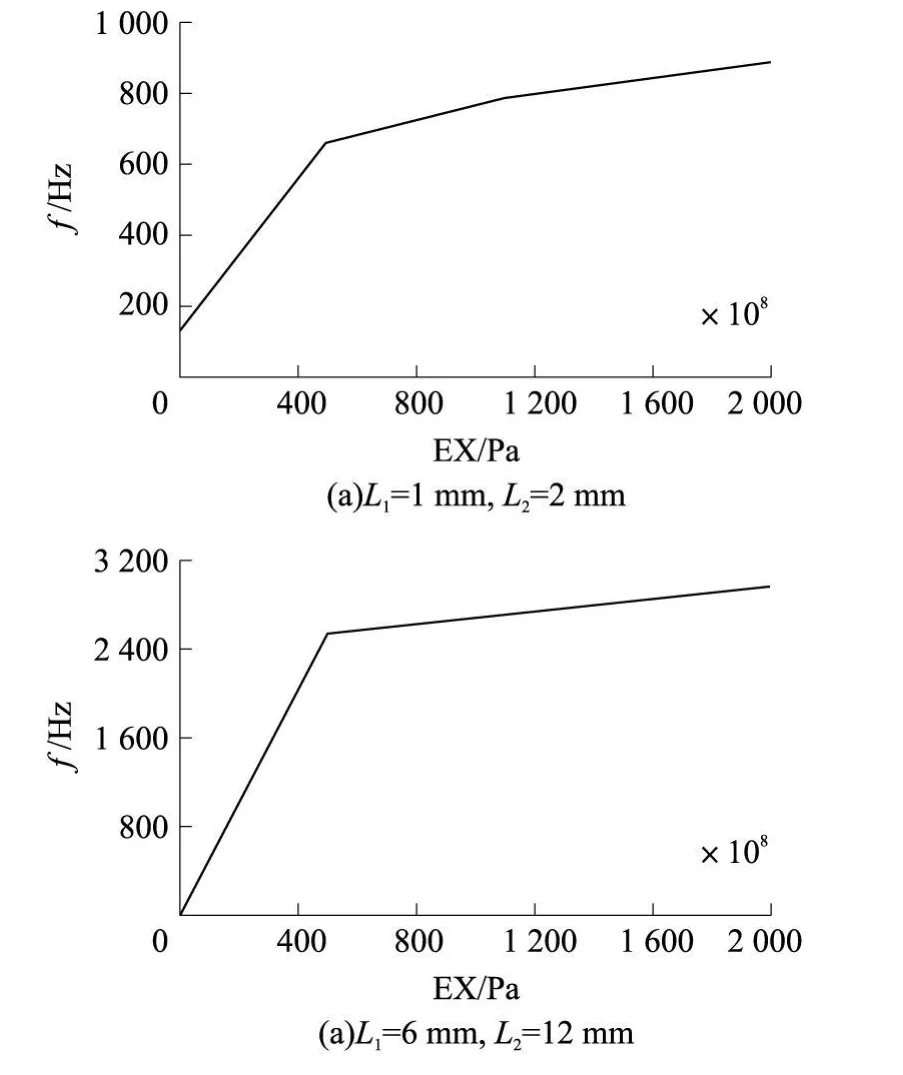
图10 弹性模量与固有频率的关系
图10表明:无论弹性膜片宽度取最小值还是最大值,固有频率都随着弹性模量的增大而增大。
3.3 内外环弹性膜参数优化
以传感器的设计目标 f≥2 kHz,u≥30 V为例阐明优化设计思想。
①通过图 7与图 10的分析得知,L1与 L2取极小值 L1=1mm,L2=2mm时,当 EX≥2 e 9 Pa,那么f≥2 kHz;当 EX≤2.4 e 10 Pa,那么 u≥30 u。 L1与L2取极大值 L1=6 mm,L2=12 mm时,当 EX>4 e 10 Pa,那么 f≥2 kHz,当 EX≤3.2 e 10 Pa,那么 u≥30 V。
②通过前面的分析知:L1与 L2取极小值 L1=1mm,L2=2mm;2 e 9 Pa≤EX≤2.4 e 10 Pa时传感器的输出电压与固有频率达到设计要求。
③仿真分析结果:当 L1=1mm,L2=2mm,EX=2 e 9 Pa时,f=2 kHz,u=50 V;当 L1=1 mm,L2=2 mm,EX=2.4 e 10 Pa时 ,f=3.5 kHz,u=30 V。
④由以上两组符合设计要求的两组参数加工出的传感器实物如图 11。

图11 传感器实物
传感器的标定结果:当 L1=1 mm,L2=2 mm,EX=2 e 9 Pa时 ,f=2.1 kHz,u=51 V;当 L1=1 mm,L2=2 mm,EX=2.4 e 10 Pa时,f=3.6 kHz,u=32 V。
4 结束语
(1)灵敏度随着弹性膜片宽度增加而增加的,但宽度变化对输出电压的影响不大。
(2)固有频率随弹性膜片宽度增加而减小,这种变化主要是由外环弹性膜片的宽度变化而引起的
(3)弹性膜片的弹性模量对传感器性能影响明显,弹性模量增大,固有频率增加但灵敏度会减小。
(4)在传感器设计时,根据优化分析结果与传感器性能要求选择合适的弹性膜参数便可完成传感器的高质量设计。
[1]韩述斌.固体物理效应与现代传感器技术[J].压电与声光,1997,19(4):235-238.
[2]LIYing-Jun,ZHANG Jun,JIA Zhen-Yuan,et al.A Novel Piezoelectric 6-Component Heavy Force/Moment Sensor for Huge Heavy-Load Manipulator's Gripper[J].Mechanical Systems and Signal Processing,2009,23(5):1644-1651.
[3]Olender D,Bymes P.A Piezoelectric Force Sensor Form ill-Scale Chip Refiners[J].Process Mechanical Engineering,2008:222-223.
[4]干方建,刘正士,任传胜,等.一种应变式多维力传感器的优化设计[J].传感器与微系统,2007,26(1):56-59
[5]娄利飞,杨银堂,张军琴,等.Ansys在 PZT压电薄膜微传感器压电分析中的应用 [J].机械科学与技,2005,24(7):875-878.
[6]董明,惠春,徐爱兰.基于 ANSYS的压电式四臂加速度计模拟分析[J].传感技术学报,2006,19(3):637-641.
[7]Dong Ming,Hui Chun,Xu Ai-lan.Analysis of Four-Beam Piezoelectric Accelerometer Based on ANSYS[J].Chinese Journal of Sensors and Actuators,2006,19(3):637-641.
[8]黄朋生,任天令,楼其伟,等.三维压电加速度传感器的设计[J].压电与声光,2003,25(5):379-381.
[9]黄亮,秦岚,刘俊,等.压电式四维力传感器的有限元分析[J].国外电子测量技术,2008,27(12):18-21.
[10]孙宝元,张贻恭.压电石英力传感器及动态切削测力仪[M].计量出版社,1985:28-33.
[11]许斌.压电式三维力传感器与多维力传感器标定装置关键技术研究[M].重庆大学,2009:21-22.
[12]博弈创作室.ANSYS9.0经典产品高级分析技术与实例详解[M].北京:中国水利水电出版社,2006,168-220.
