动态灰色模型的滑坡位移时间预测方法研究

吴银亮，刘艳敏，祝艳波

(1.中交第二公路勘察设计研究院有限公司，武汉 430052;2.中国地质大学(武汉)，武汉 430074)

滑坡是坡体因多种因素耦合变形，最终被某些诱发因素激发失稳，产生滑动的一种地质灾害。随着我国工程建设事业的发展，滑坡失稳频度、范围、强度均表现出上升趋势。由于受多因素耦合作用，滑坡失稳时间的判定及预测至关重要，却又是工程研究中一大难点。

灰色理论是在20世纪系统论、信息论及控制论蓬勃发展的大背景下诞生的。它是介于随机不确定性统计理论与认知不确定性模糊理论之间的一门新兴学科。最早由我国学者邓聚龙教授于20世纪80年代提出。一经问世，便受到了中外学者的广泛关注，现已成为一门横断面宽、渗透力强的新兴学科。灰色理论从诞生之日起，便因它小样本快速建模性质而被广泛地应用到变形监测分析与预报领域，特别是针对于贫信息建模具有较高的拟合度和准确度，因此通常作为监测初期少数据量预报工作的首选。但其也存在着波动数据建模预测失真与原点误差影响显著问题，针对此问题提出了动态灰色模型。动态灰色模型是在原有灰色静态模型的基础上，引入了固定维度概念与新息优先原则，它对原有静态建模方式进行了动态改进，对预测问题具有更高的拟合精度。本文将动态灰色模型引入滑坡位移变形进行预测，通过黄茨滑坡实例，验证了动态灰色模型在滑坡预测研究中的灵活性和准确性。

1 动态灰色预测模型基本原理

动态灰色模型基于维度不变与递补动态思想，将对模型影响显著的原点误差项排除在维度范围之外，所以其预测精度相比静态预测明显提高，而动态思想也符合事物的发展规律，其具体建模过程如下:对于非负离散数据序列x(0)

式中，n为自然数，表示序列长度。

对x(0)进行一次累加生成(AGO)，得

由一阶微分方程

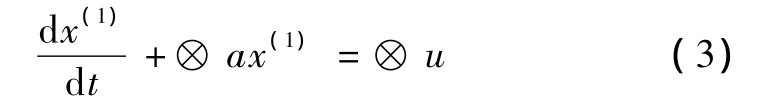
其中，t为时间参量，a，u为待定参数，⊗为灰标识。

由最小二乘法得待定参数的最优估计值

式中，T为矩阵转置。

其中e为自然对数。

对x(1)(t+1)作累减生成(IAGO)，得

此时，去掉x(0)(1)，加入估计值(t+1)，组成新的离散数列，即

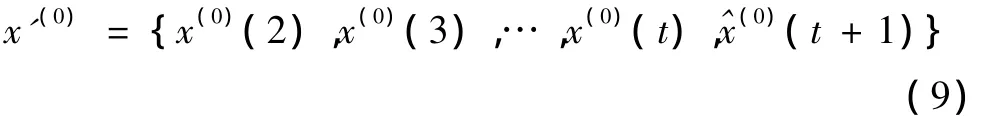
然后由上面的离散数列再次建立GM(1，1)模型，预测下一时刻的值。

由于等维信息灰色动态模型的数据信息是实时引入的，因此它能够不受原点误差的影响，实时地反映所研究物体的状态变化。

2 黄茨滑坡概况

2.1 黄茨滑坡工程概况

黄茨滑坡位于盐锅峡镇黄茨村北部黑方台南缘，从坡脚到苔原顶面高差百米，坡脚是一常年流水的水渠，紧靠水渠南侧即为人口密集的居民区。距坡脚百米之遥是兰州通往盐锅峡化工厂的盐锅峡水电站的公路，滑坡与公路之间原有居民63户，300余人。滑坡前缘直抵黄茨村，直接威胁村民生命财产安全。

该滑坡滑动受多方面因素控制，滑动规模大且复杂。滑坡体积近600万m3，基岩面以100°～200°倾角倾向临空面，易导致沿基岩面的顺层滑动。大量的灌溉活动，使得该工作区水量增加至降雨量的40～50倍，地下水水位抬升，软弱结构面不断被浸润、软化，土体强度降低，在自重压力作用下，向临空面蠕滑变形。

2.2 监测数据分析

滑坡变形发展由缓慢变形—加速变形—明显减速阶段—加速变形四阶段构成。加速变形阶段主要出现在冬灌后的12月的中下旬，从1月初至1月中旬，除个别检测点，其余均表现出来明显的减速阶段，此即为滑坡克服静摩擦力，岩体抗剪强度峰值亦达到最大，滑坡准备滑动的表现。越到后期，各监测数据位移—时间曲线越表现出明显的同步性，此多为边坡整体大规模失稳的预兆。当滑坡经过减速阶段进入加速变形之后，滑坡即由克服静摩擦力转化为克服动摩擦力而滑动。

3 动态灰色模型黄茨滑坡位移时间预测

3.1 基本思路

了解滑坡变形破坏影响因素，对变形监测数据进行初步分析，在此基础上，引入动态灰色模型进行滑坡位移时间预测。选用维度为7(一个星期)，应用累积变形量进行预测，得到第8～27 d的预测结果。由累计变形量反推位移变形量，同时，应用静态灰色模型进行计算预测，并将静态预测结果和动态预测结果与真实值进行比较得到残差项，通过残差平方和得到精度值，用精度值评价计算结果的准确度与可靠性。

其中，v为残差，［vv］为残差平方和，n为预测总数。

3.2 动态灰色模型预测预报

本次主要采用黄茨滑坡1994-11-25—1994-12-21监测数据。设计维度为7，由累计变形量进行位移—时间预测，并计算累计变形量残差，预测结果见表1。

应用残差预测结果，引入公式(11)，计算累计位移变形量灰色预测精度。计算结果见表2。做累计变形量预测曲线(图1)、累积变形量残差曲线(图2)，同时添加一次预测趋势线。

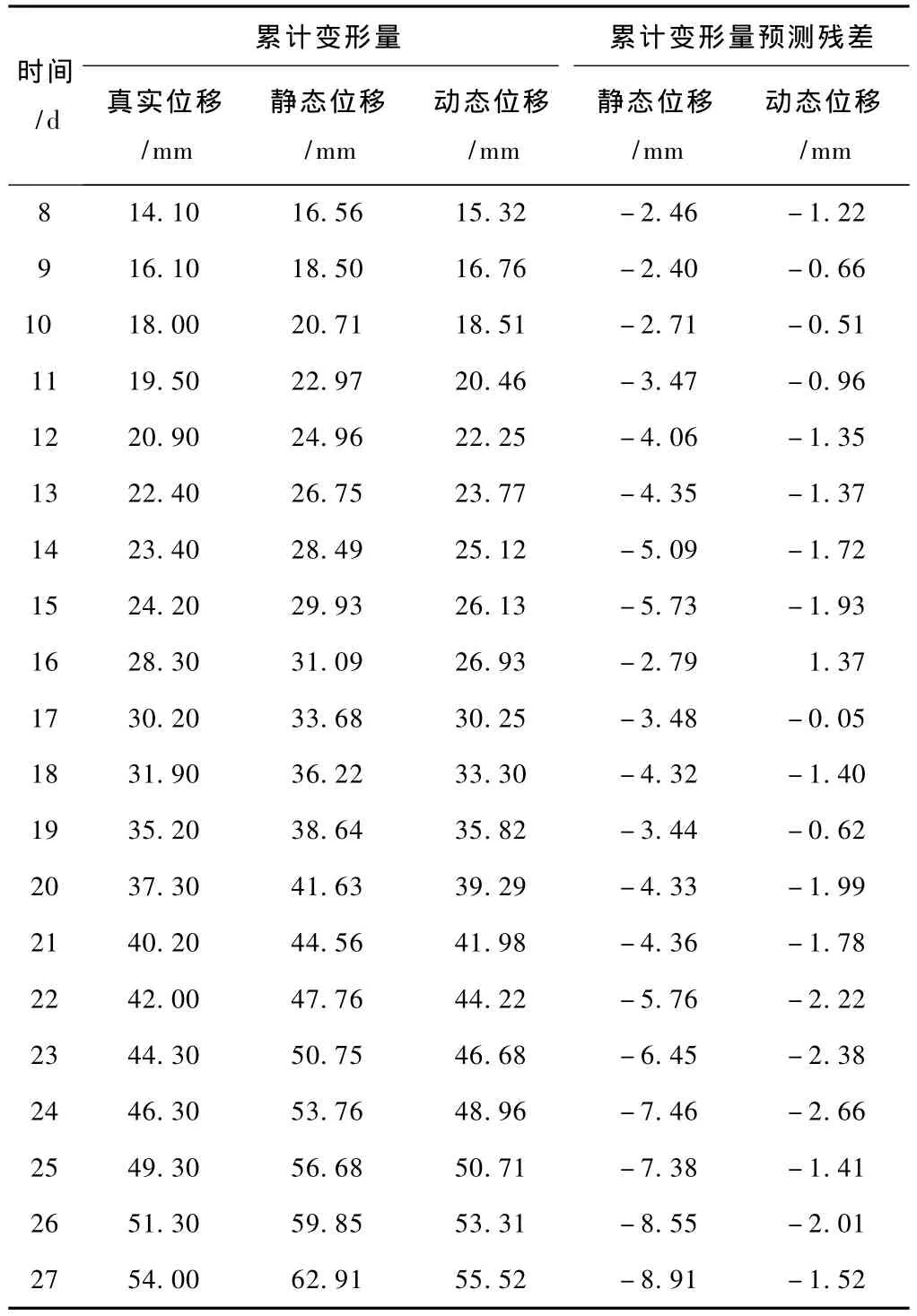
表1 累计位移变形量预测结果

表2 累积位移变形量灰色预测精度结果 mm

通过静态累积变形量灰色预测与动态累积变形量灰色预测的比较，可以得出:动态灰色预测相比静态灰色预测，更贴近真实值，且其残差在0附近均匀分布(－2～2 mm)，而静态灰色残差分布呈偏峰分布(－10～－2 mm)，且跳跃较大。因此，动态灰色预测相比静态更加稳定准确。

图1 累计位移变形量预测曲线

图2 累积位移变形量预测残差曲线

由累计变形量预测结果反推变形量，其结果见表3，计算变形量预测精度(见表4)。做累计变形量预测曲线(图3)，同时添加一次预测趋势线。

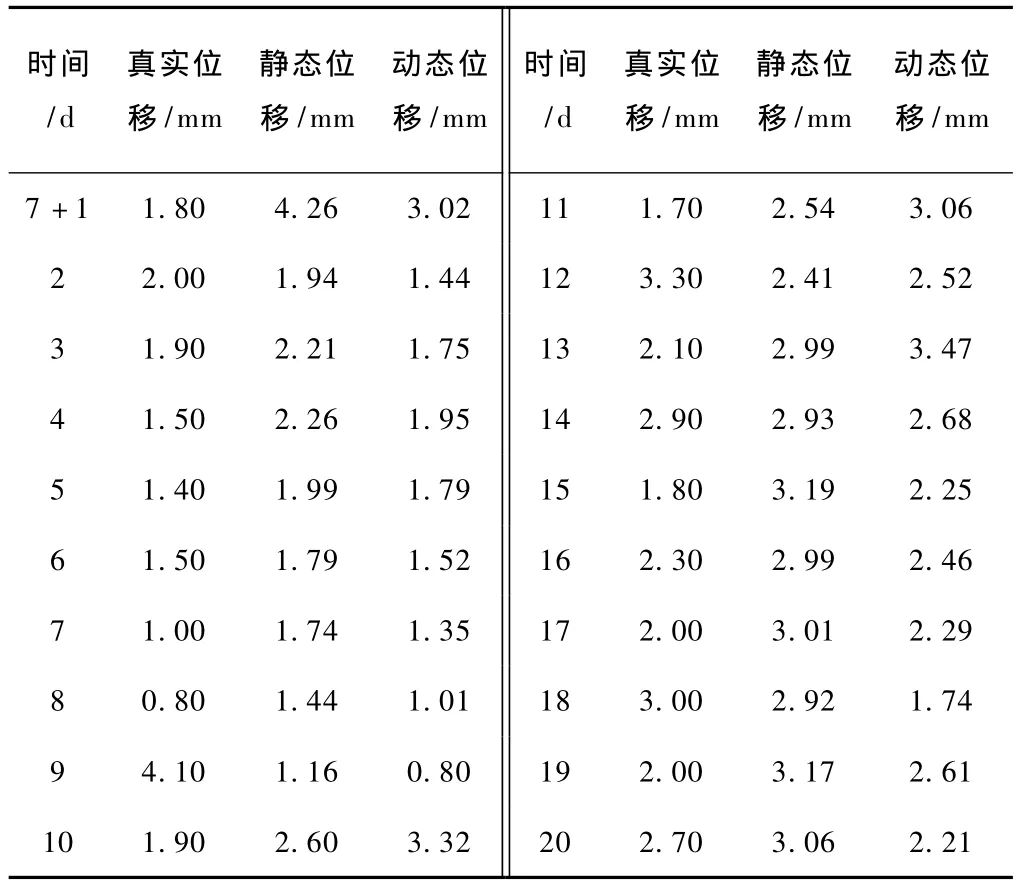
表3 位移变形量预测数值(由累计变形量反推位移变形量数值)

表4 位移变形量灰色预测精度结果 mm

图3 位移变形量预测曲线

从以上研究分析中可以得到以下结论:

1)1994-11-25—1994-12-21时间段存在明显的从均速蠕变、加速蠕变至减速位移再至加速蠕变的规律性。由图3曲线可知:该滑坡在1994-12-09之后累积位移量明显增加，故滑坡在此阶段之后可能发生滑动。

2)选取1994-11-25—1994-12-21时间段内数据所做累计变形量预测结果反推变形量所得试验结果与实际情况差距较小，可靠度高，对于波动较大的滑坡监测数据，动态灰色模型较静态灰色模型预测的准确度明显提高，并能够很好地拟合滑坡并行破坏的发展趋势，预测残差、精度均较小。

4 结论

本文针对传统静态灰色模型在滑坡位移时间预测中存在的一些弊端，引入了动态灰色模型，通过对黄茨滑坡1994-11-25—1994-12-21监测数据的预测结果表明:动态灰色预测相比静态灰色预测更贴近真实变形情况，且模型稳定，预测残差分布均匀。动态灰色模型灵敏度高，可以应用于滑坡临滑期预测。在研究过程中发现，灰色模型对于波动性较大的数据，预测效果表现出一定的滞后性，因此，对于灰色理论研究，采用累计变形量进行预测，反推位移变形量，预测效果较好。

［1］邓聚龙.灰色系统理论教程［M］.第一版.武汉:华中理工大学出版社，1990.

［2］邓聚龙.灰预测与灰决策［M］.第一版.武汉:华中理工大学出版社，2002.

［3］尹晖，丁窘，张琰，等.灰色动态预测方法及其在变形预测中的应用［J］.武汉测绘科技大学学报，1996，21(1):31-35.

［4］李宗坤，郑晶星.GM(1，1)等维新息模型在土石坝沉降预测中的应用［J］.水利水电技术，2003，34(7):74-75.

［5］王利，张双成，李亚红.动态灰色预测模型在大坝变形监测及预报中的应用研究［J］.西安科技大学学报，2005，25(3):328-332.