自锁型预应力锚索的应用

刘庆元

(中铁西北科学研究院有限公司 南方分院，深圳 518048)

随着我国基础建设项目的高速发展，大量的锚固工程得到应用，岩土锚固工程除在地下工程、边坡工程、结构抗浮工程、深基坑工程中继续保持着良好的发展态势外，在重力坝加固工程、桥梁工程以及抗倾覆、抗地震工程中也有了较大的进展。除了传统的锚固结构形式外，大量的新型锚固结构不断研制成功并得到应用，例如块硬水泥锚杆、扩头地锚、屈服锚杆、自钻式注浆锚杆、可回收锚杆、传力可控型锚杆以及自锁型预应力锚索等。

自锁型预应力锚索是一种新型预应力锚索结构，在锚固体系上施加主动荷载时，张拉荷载在锚具外表面处与锚固段产生的抵抗荷载(简称锚固荷载)平衡;张拉机具卸载过程中，各自锁荷载之和与反力结构上外锚头的剩余荷载一起与锚固荷载进行平衡;当自锁器发挥作用且张拉机具全部卸载后，作用在反力结构上的只有锚固荷载减去自锁荷载后的剩余荷载，其内力也相应减小。

与普通锚固结构相比较，自锁型预应力锚索应力场具有三大特点:①反力结构上的剩余荷载比锚固荷载小甚至为零，不但可减小反力结构，而且反力结构下地基应力值也相应减小，从而对坡面浅表层的岩土体干扰也小，可大幅减小因该部分岩土体变形调整引起的预应力损失。②自锁器对张拉段地层施加主动黏结应力，且作用方向为沿锚索轴向朝向坡体内部，有利于保持该部分岩土体的稳定。③锚固荷载由自锁荷载和反力结构上的剩余荷载共同平衡，即锚固段抵抗能量场=张拉段自锁能量场+附加能量场，能充分提高结构各部分的利用率。

因此，自锁型预应力锚索结构充分利用张拉段地层能量场，改善锚固应力场分布，具有荷载分布均匀、降低反力结构规模或取消反力结构、施工便捷、延缓锚固荷载损失、预防预应力锚索突发事故、节约造价、便于环保等优点，在抢险工程和环境保护要求较高的领域具有明显的优越性。

1 自锁型预应力锚索的设计方法

1.1 自锁型预应力锚索的设计参数

目前应用较多的预应力锚索结构有普通拉力型、普通压力型、拉力分散型、压力分散型以及拉压复合型，主要是依据锚固段的结构进行分类，与这些预应力锚索结构类型相似，自锁型预应力锚索结构的设计也包括如下内容:

1)锚固荷载计算

目前采用较多的是简化的Bishop条分法，其计算公式为

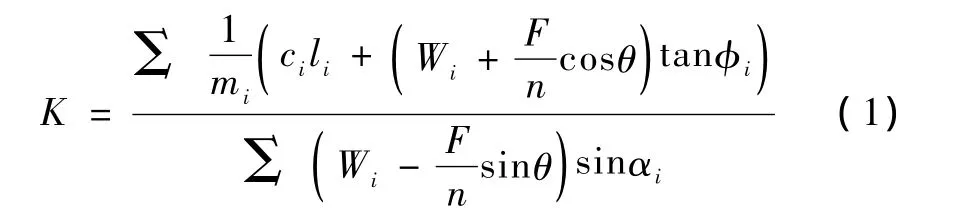
式中 K——稳定性系数;

mi——倾角影响系数;

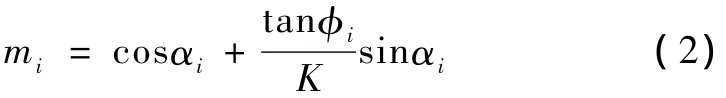
ci——第i条土条的有效内聚力，kN;

li——第i条土条沿滑裂面的长度，m;

Wi——第 i条土条的重力，kN;

F——岩土体的加固荷载，kN;

n——岩土体被分割的条块数;

θ——加固荷载F与水平面的夹角，°;

αi——第i条土条滑裂面与水平面的夹角，°;

φi——第 i条土条的有效内摩擦角，°;

2)预应力锚索规格、长度及锚固段长度计算

该部分设计计算包括钻孔孔径、钻孔倾角、组成预应力锚索的钢绞线类型及束数、注浆体强度、锚固段长度和预应力锚索总长度等，相关规范或文献说明较多，本文不再赘述。

3)反力结构计算

反力结构对应的剩余荷载为

其中，F为反力结构上的作用荷载，kN。Fzi为第i单元的自锁荷载，kN。

结构设计方法则根据弹性地基梁法可计算出反力结构的挠度ω、弯矩M和剪力Q分别为

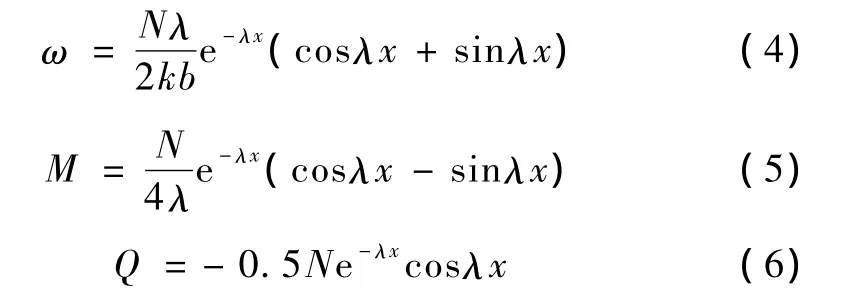
式中 k——温克尔地基系数，kN/m3;

λ——弹性地基的柔度特征值，m－1;且

x——沿梁长轴方向离梁端的距离，m;

b，Ec，I——分别为反力梁的宽度，m、弹性模量，kN/m2、惯性矩，m4。

然后可直接利用现行规范进行有关设计计算。

1.2 自锁参数设计

自锁参数设计是自锁型预应力锚索结构新增的设计内容，自锁参数包括自锁器离孔口的最小距离和各自锁单元的自锁段长度、自锁荷载，其参数设计直接关系到自锁荷载能否实现，从而实现自锁锚固结构的目的。

1)自锁器离孔口的最小距离Lmin

由于在自锁单元内距离自锁器较近的部位会出现应力峰值，为了保证自锁器的安全使用，其应力峰值不应超过孔周岩土体的抗剪强度，否则将引起孔周岩土体破坏，从而有可能导致自锁失效，其应力峰值τmax计算公式为

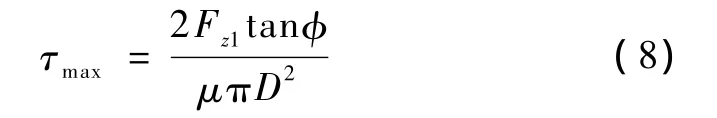
其中，Fz1为第一单元(即靠近孔口单元)自锁荷载，kN;D为锚固体的直径，mm;φ为岩土体的内摩擦角，°;μ为岩土体泊松比。

式(8)中，τmax及 Fz1均为未知量。为此，需先绘制孔周岩土体的抗剪强度τ0与轴方向距离孔口的距离y之间的曲线，然后参考第一单元自锁荷载分担锚固荷载的比例要求，分别绘制不同比例时对应的 τmax水平直线，该水平直线与 τ0—y曲线的交点所对应的y值即为该自锁荷载时对应的Lmin。综合比较选择合适的第一单元自锁荷载，即可计算出自锁器距离孔口的最小距离 Lmin。

2)自锁段长度

当张拉段地层为单一地层时，其自锁段长度可采取均匀分布的方式，且

其中，lz为自锁单元长度，m;Lz为张拉段长度，m;Lmin为自锁器离孔口的最小距离，m;n为自锁单元个数。

当张拉段包含多种地层时，首先分别对张拉段长度和弹性模量进行加权平均，再按加权平均的弹性模量换算虚拟张拉段长度，然后对虚拟张拉段长度计算虚拟自锁长度，最后依据弹性模量比换算成实际地层对应的自锁长度。假设张拉段包含m种地层，第i种地层对应的长度为li，其弹性模量为 Ei，则有

其中，L'z为换算张拉段长度，m;E'为地层的换算弹性模量，MPa;l'z为换算自锁单元长度，m;liz为第 i单元自锁单元长度，m。

当某一自锁段跨越不同地层时，仍按弹性模量比进行换算，即虚拟自锁长度减去前一地层的剩余虚拟长度后，再换算成对应地层的实际长度。

3)自锁荷载

对应各自锁单元的自锁荷载计算公式可直接推导如下

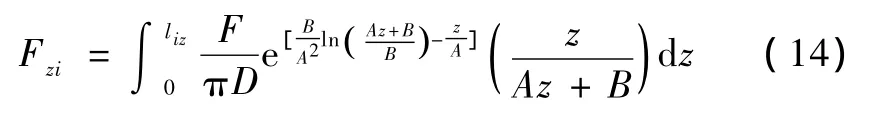
式中 A，B均为简化系数，

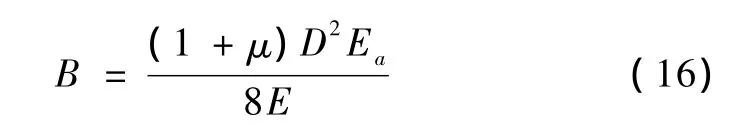
Ea——锚固体的换算弹性模量，MPa;

E——岩土体弹性模量，MPa;

z——各自锁单元内沿孔轴方向距离自锁器的距离，m。

2 自锁型预应力锚索的实施

自锁型预应力锚索的实施基本与常规预应力锚索相同，实施的重点在于自锁器的安装和张拉锁定两个关键工艺环节。

2.1 自锁器的安装

自锁器的安装步骤为:①根据设计资料确定每单元自锁器的位置(若锚固段设计为荷载分散型的，自锁单元应与受力单元一致)，并在相应钢绞线张拉段上做出明显标志。②对于无黏结钢绞线，应在安装自锁器的标志位置处开始向锚固端方向约10 cm段剥除PE套并将防腐油脂擦除干净。③依次将钢绞线、注浆管和回浆管穿过自锁器，并将各单元自锁器固定在标志位置。

2.2 张拉锁定

由于自锁型预应力锚索为新型结构，尤其是锚固荷载由自锁荷载和反力结构共同进行平衡，其张拉锁定工艺与普通预应力锚索有较大差异，具体施工工艺为:

1)张拉机具采用复合张拉系统，即主张拉机具和辅助顶推机具。主张拉机具可采用液压千斤顶，而辅助顶推机具构造如下:①承压套由钢质材料组成，状似中部开口圆筒，两端面附有受力钢板，并且在钢质圆筒外设有加劲钢肋板。②固定装置主要用于固定顶推系统，使其固定在承压套上，并能自由工作。固定装置主要采取滑动键槽结构或螺栓结构。③顶推系统主要为一小型液压千斤顶，额定荷载为300 kN，行程为150 mm。复合张拉系统结构见图1。

2)首先从钢绞线外露端头分别装上锚具、限位板，再安装辅助顶推机具，最后安装张拉千斤顶及工具锚和夹片，由于自锁型预应力锚索按自锁单元进行分单元张拉，因此工具锚内只能安装被张拉单元的夹片，而且为了实现自锁效果，张拉过程中反力结构上的锚具不能安装夹片。

3)按照普通预应力锚索的张拉规程对一个自锁单元的钢绞线进行张拉，自锁单元的张拉顺序为从坡体内向外进行。

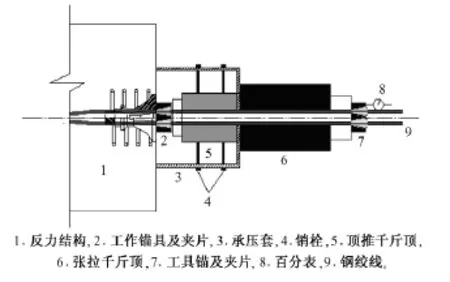
图1 复合张拉系统结构

4)当一个自锁单元张拉至设计荷载并持压稳定后，对张拉千斤顶缓慢卸载，当卸载至该单元的反力结构上的剩余荷载时，停止卸载，并稳定该荷载;然后在反力结构上的锚具内安装该单元的夹片，启动顶推系统，直至反力结构上的锚具夹片锁紧钢绞线(一般情况下，夹片环行槽基本与锚具外表面平齐)，最后对顶推系统卸载。

5)按照3)和4)的操作方法依次对各自锁单元进行张拉锁定，即可完成对整根自锁型预应力锚索的张拉锁定。

3 自锁型预应力锚索的自锁效果

为了探索自锁型预应力锚索的自锁效果及运营状况，选取福建省境内某高速公路一处滑坡工程实例进行监测，该滑坡锚固段地层为强风化凝灰熔岩，张拉段地层为坡残积土层及砂土状强风化凝灰熔岩，每根预应力锚索采用3单元自锁，自锁荷载及注浆体轴向应力(1断面紧贴自锁器，2断面距离自锁器1.5 m)监测结果见图2至图7。

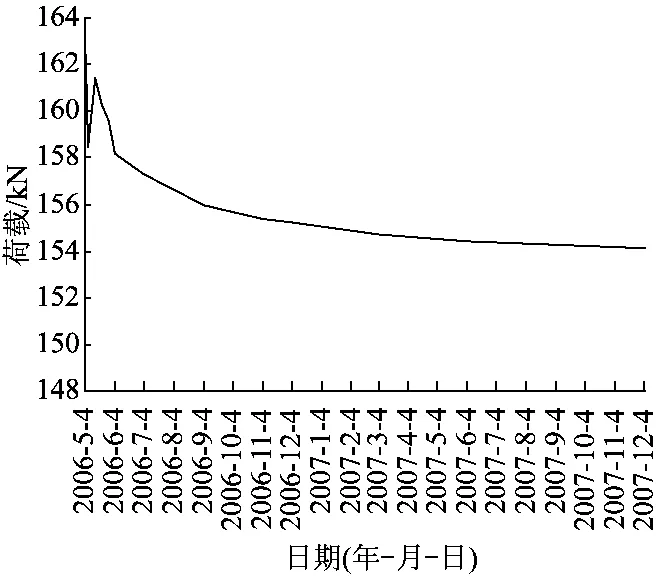
图2 MS1单元自锁荷载长期变化曲线

从上述长期监测曲线可总结出如下规律:①自锁荷载在锁定的初期有一个小幅震荡，然后呈缓慢衰减趋势，半年后基本处于稳定状态，表明自锁效果良好。②注浆体压应力与到自锁锚固段底端距离成非线性关系，回归公式可描述为σ=aebx(a、b分别为与荷载、孔周岩土体和锚固体材料力学性质有关的常数)。③压力峰值出现在自锁器的自锁锚头处，其峰值大小受岩土特性、注浆体与岩土界面黏结力、自锁器位置和注浆体强度的影响而变化。

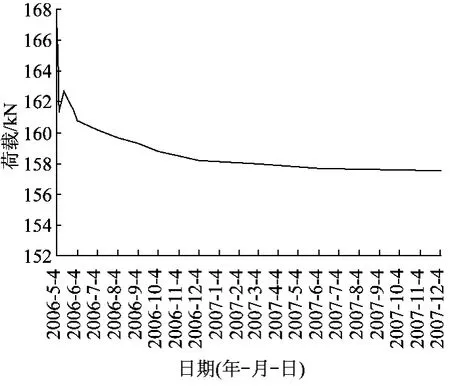
图3 MS2单元自锁荷载长期变化曲线

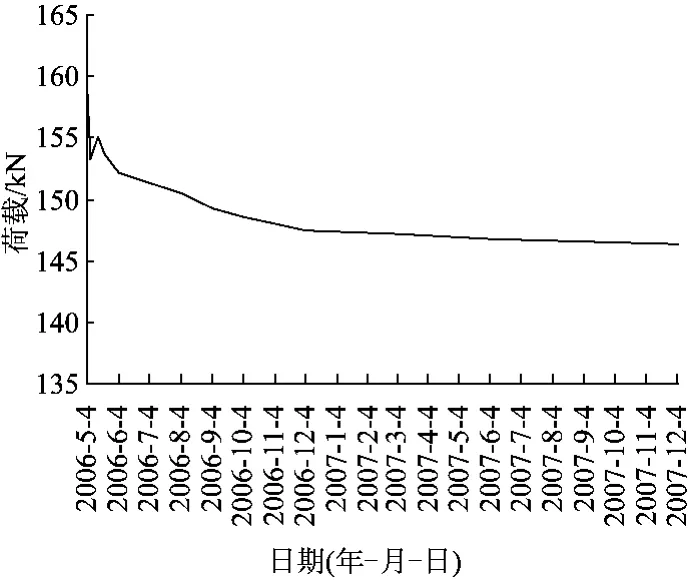
图4 MS3单元自锁荷载长期变化曲线

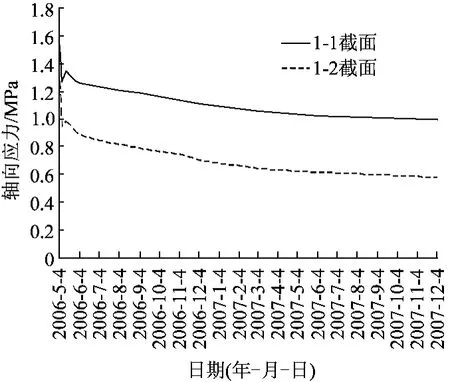
图5 MS1单元注浆体轴向应力长期变化曲线

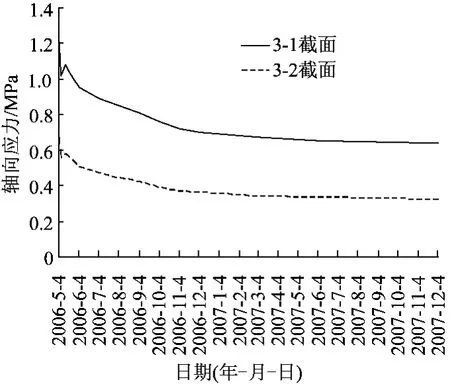
图7 MS3单元注浆体轴向应力长期变化曲线

4 结论

自锁型预应力锚索结构具有荷载分布均匀、降低反力结构规模或取消反力结构、施工便捷、延缓锚固荷载损失、预防预应力锚索突发事故、节约造价、便于环保等优点，在抢险工程和环境保护要求较高的领域具有明显的优越性。工程实践证明，自锁型预应力锚索能有效实现锚固荷载的自锁效果，其自锁荷载变化趋势与锚固荷载一致。自锁型预应力锚索的注浆体轴向应力较之常规预应力锚索有较大幅度的降低，有利于保持注浆体的整体性，在使用期限及防腐等方面具有明显优势。自锁型预应力锚索是一种新型结构，对于张拉段地层强度较低的条件下其适用性与经济性需进一步探索。

［1］中国岩土锚固工程协会.岩土锚固新技术［M］.北京:人民交通出版社，2002.

［2］尤春安，战玉宝.预应力锚索锚固段的应力分布规律及分析［J］.岩石力学与工程学报，2005，24(3):925-928.

［3］周忠海.关于对预应力锚索加固效应的看法［J］.山西建筑，2008，34(5):82-83.

［4］刘伟平，扶名福，罗小艳.锚索的极限抗拔力分析［J］.铁道建筑，2010(5):74-75.

［5］付文斌，陈泰霖，王安明，等.压力分散型锚索现场试验与分析［J］.铁道建筑，2009(12):86-88.

［6］张发明，陈祖煜，刘宁.岩体与锚固体间黏结强度的确定［J］.岩土力学，2001，22(12):470-473.