微粒群算法在SBR污水处理系统中的应用

张亚鹤

(同济大学，上海 201804)

污水处理系统就是采用工程技术措施对生产废水进行处理,减轻乃至消除污水对环境的污染,改善和保持水环境质量,保障人民健康以及有效地、合理地综合利用水资源。污水处理过程是一个具有大时滞、非线性、强干扰的复杂控制对象,要控制的参数例如温度、pH值、生物需氧量(Biochemical Oxygen De-mand,BOD)、溶解氧浓度(Dissolved Oxygen,DO)值等之间相互影响并有大的滞后,同时各个参数随生产的变化而不确定地变化。污水处理系统需要一系列行之有效的处理技术,除了加强污染源的控制和管理,采用不排或少排废水的先进工艺外,还应开发多种污水处理的新工艺算法、新设备、新材料,并利用当代先进技术,将计算机技术引入到污水处理系统中,把现代先进的控制策略[1]应用于污水处理系统中,使污水处理日益精确化、快速化,并不断连续化、自动化及网络化,从而从局部到全局提高污水处理效率,降低污水处理成木。近年来发展起来的智能控制在复杂控制对象中的成功应用为这类系统的自动控制提供了一种新方法[2]。本文将详细介绍微粒群算法在污水处理控制系统的应用,以方便读者的进一步研究。

1 SBR污水处理系统

间歇式活性污泥法或序批式活性污泥法(Sequencing Batch Reactor Activated Sludge Process,SBR)作为一种新技术不论在工业企业还是城市污水处理中均得到了广泛的应用。

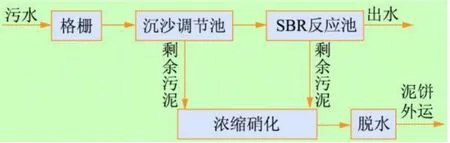
图1 SBR操作流程图

SBR操作过程主要由进水(Fill)、反应(Aerate)、沉淀(Settle)、出水(Discharge)和空闲(Idle)5个阶段组成,操作流程如图1。从污水进入到待机时间结束作为一个周期,在一个周期内,所有的操作都在SBR反应池中依次进行,反应池中有曝气装置和搅拌装置。SBR反应池在一定时间间隔内充满污水,处理结束后,把上清液从反应池中排出;把多余的生物污泥浓缩硝化、外运,而把适量的底部生物污泥留于反应池内,用于下次污水处理。这样周期性的运行,就构成了SBR处理工艺。在处理过程中,通过鼓风机向反应池曝气,来补充反应池内的溶解氧。SBR反应池中溶解氧浓度的高低直接影响有机物的去除效率和活性污泥的生长,所以DO浓度是SBR控制的重要控制参数[1],而且DO仪的构造简单、性能稳定、响应迅速、价格便宜便于与计算机接口,在本文中均以DO为被控参数。

2 微粒群算法

1995年,Kennedy和Eberhart提出一种较为新颖的优化算法——微粒群算法(Particle Swarm Optimization,PSO)[3],该算法是一种基于群体智能(Swarm Intelligence,SI)的优化算法,即模拟鸟群觅食的过程。在PSO中,每个优化问题的解都是搜索空间中的一只鸟,称之为粒子(Particle)。所有的粒子都有一个由被优化的函数决定的适应度值(Fitness Value),每个粒子还有一个速度(Velocity)决定它们飞翔的方向和距离。PSO初始化为一群随机粒子,然后粒子们就追随当前最优粒子在解空间中搜索找到最优解。在每一次迭代飞跃中,粒子通过跟踪两个“极值”来更新自己。第一个就是粒子自己找到的最优解,称个体极值(Pbest);另一个极值是整个粒子群目前找到的最优解,称全局极值(Gbest)。

假设用X=(Xi1,Xi2,…,Xid)表示第i个粒子,其中d是粒子的维数,它经历过的最好位置表示为Pg=(Pi1,Pi2,Pi3,…,Pid),而整个群体经历过的最好位置表示为gb=(Pg1,Pg2,Pg3,…,Pgd)。粒子i的速度用V=(Vi1,Vi2,…,Vid)表示。对于每一代个体,在找到两个最优值时,粒子根据如下公式来更新自己的速度和位置,即

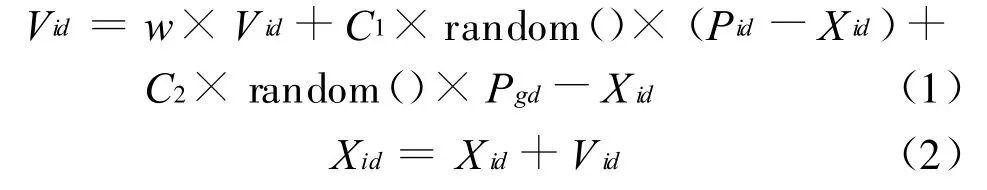
式中,w为惯性权重,random()是介于(0,1)之间的随机数,C1,C2是学习因子(或者称为加速度系数)。另外,粒子的每一维速度都会被一个最大速度Vmax限定,如果某一维的速度更新后的速度超过用户设定的Vmax,那么这一维的速度就被限定为Vmax。

3 微粒群算法对污水处理PID控制系统的优化

比例—积分—微分(Proportion Integration Differentiation,PID)控制器具有结构简单、容易实现、控制效果好、鲁棒性强等特点,而且原理简明、参数物理意义明确、理论分析体系完整且为工程界所熟悉,因而在工业过程控制中至今仍得到广泛应用(占90%以上)。PID参数的整定与优化一直是人们感兴趣的问题,目前已有的方法有传统的Z2N法、频域法等以及新兴的遗传算法。其中,遗传算法是一种较好的PID参数优化方法,可是遗传算法仍存在容易发生“早熟”、收敛慢、性能对参数有较大的依赖性等缺点,限制了它的应用。粒子群优化算法是一类随机全局优化技术,算法通过粒子间的相互作用发现复杂搜索空间中的最优区域,能取得比传统参数整定方法更令人满意的结果。PSO优化PID控制系统如图2所示。DOs表示溶解浓度DO的设定值。

PID算法由下式描述:

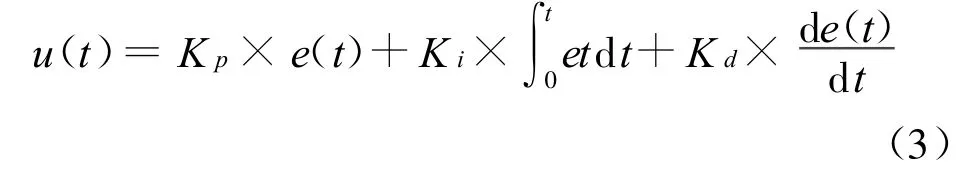
图2 PSO优化RBF神经网络程序流程图

PSO-PID参数整定就是利用PSO算法来优化上述的3个参数,其本质是基于一定目标函数的参数寻优问题。可令群体中的粒子数为m,每个粒子的维数为D=3,即由PID控制器的3个参数Kp,Ki,Kd组成,则群体可以用一个m×D的矩阵来表示。目标函数即适度函数本文采用了能反映系统调节品质的ITAE的倒数,ITAE是时间乘绝对误差的积分[4]。

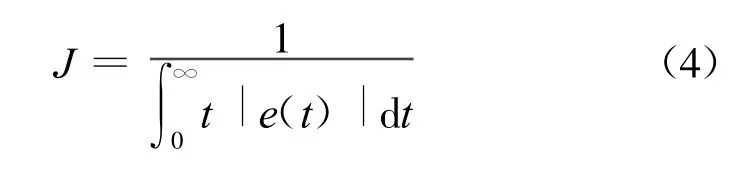
式中,e(t)为当前微粒产生的误差。

用Ji表示微粒当前的适应值,Jibest表示个体历史最好适应值,Jgbest表示全局经历过的最好适应值。

最优参数的整定步骤如下:

(1)根据经验确定PID参数的范围以及PSO算法的控制参数Vmax后,在参数范围里初始化一群微粒即随机产生位置Xi与速度Vi;

(2)确定每个微粒的适应值Ji,利用单位阶跃响应通过仿真运算得到ITAE后求出Ji;

(3)对每个微粒:如果 Ji＞Jibest,则 Jibest=Ji,Pi=Xi;如果 Ji＞Jgbest,则 Jgbest=Ji,Pg=Xi;

(4)利用式(1)和式(2)更新微粒的速度与位置;

(5)如未达到结束条件(如预设的代数),返回步骤(2)。

4 微粒群算法对RBF神经网络的优化

径向基函数(Radial Basis Function,RBF)神经网络是一种具有全局逼近能力、结构简单、计算量少的多层前馈神经网络,目前已被广泛应用于模式识别、自动控制、函数逼近、非线性时间序列预测等多个领域。RBF神经网络的非线性映射能力体现在隐层径向基函数上,其特性主要由径向基函数的中心确定。基函数中心的确定方法有多种,如正交优选法、递推Givens变换算法等。正交优选法可以自动确定最佳的隐层数目和网络输出权值,但隐含层中心点取值为输入数据,因此很难反映出系统真正的输入输出关系,并且初始中心点数太多,在优选过程中会出现数据病态现象,当正交过程中所选取的正交向量超过一定数目后,将难以进一步选出正交向量;递推Givens变换算法虽然解决了递推最小二乘的数据病态问题,但是计算量较大,并且在学习过程中不能找到网络实际所需的隐层神经元数目。粒子群算法在函数优化和神经网络权值训练等方面都有很好的表现[5],其对RBF神经网络的编码和适应度函数如下。

(1)编码方式。微粒编码采用实数编码,其中应包括基函数中心值、网络权值和方差,在污水处理过程的优化设计中选取了溶解氧DO浓度作为主要控制变量,根据适应度函数溶解氧DO预测的准备性动态调整各个参数。

(2)适应度函数获取。在粒子群算法的实际运用中,适应度函数是由目标函数变换而成的。根据本污水处理系统,选取相应期望输出值和神经网络输出值差的平方为适应度函数。

这里选取在污水处理过程中的一组数据通过RBF网络进行建模,化学需氧量和曝气量为输入,预测溶解氧DO输出的值。然后再通过PSO算法对RBF网络进行优化,进而通过微粒群优化的RBF网络建模预测溶解氧的值。图3为经过优化的RBF网络和未经优化的RBF网络对比图。

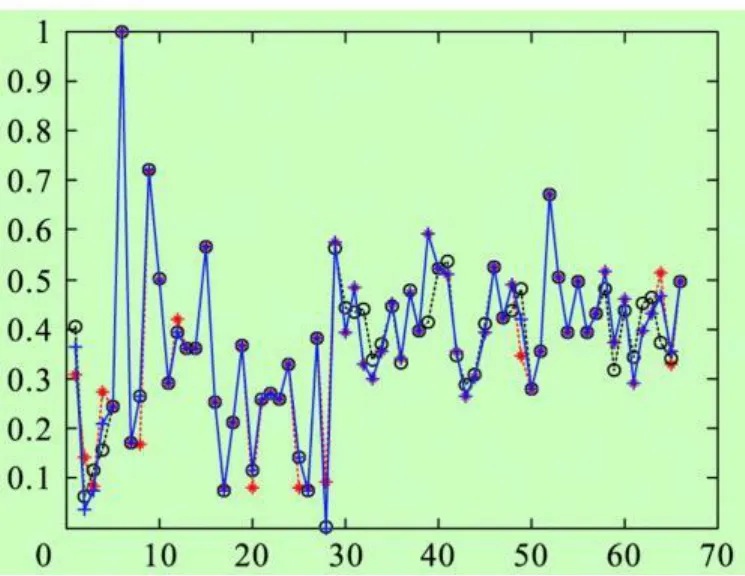
图3 RBF和PSO-RBF对溶解氧DO的预测曲线

图3中,蓝色为实际溶解氧DO曲线,红色为RBF预测溶解氧DO曲线,黑色为经过优化的RBF预测溶解氧DO曲线。由上图可以看出经过优化的RBF网络对数据预测的精度有了很大的提高,也说明了PSO算法在RBF优化中的适用性。

5 微粒群算法对反向传播神经网络的优化

反向传播(Back Propagation,BP)神经网络是一种有效的自学习神经网络,具有一些独特的性质:信息的分布式存储和并行处理,具有自组织、自学习能力等,已经被广泛应用于模式识别、知识工程、智能控制等方面。尽管在诸多应用领域取得了巨大的成功,然而仍存在着一些问题。①学习算法的收敛速度慢;②局部极小问题;③BP神经网络隐层神经元的个数选取目前尚无理论上的依据,只能根据经验选取。

PSO用于训练BP神经网络的方法[6]是:粒子群中每个粒子的位置表示BP网络中当前迭代中的权值集合,每个粒子的维数由网络中起连接作用的权值的数量和阈值个数决定。以给定训练样本集的神经网络输出误差作为神经网络训练问题的适应函数,适应度值表示神经网络的误差,误差越小则表明粒子在搜索中具有更好的性能。粒子在权值空间内移动搜索使得网络输出层的误差最小,改变粒子的速度即更新网络的权值,以减少均方误差。通过这种方式,PSO优化搜索训练神经网络的权值和阈值来获得更小的均方误差。每次迭代过程中产生均方误差最小的粒子为目前全局最优的粒子。BP网络采用隐层数目可变的方法,即一开始放入较多的隐层节点,随着训练过程的进行,逐步修减掉在网络训练中不起作用的节点。对于每一神经元,若在训练过程中,其连接权的数值的绝对值小于事先确定的数值,则删除此神经节点。算法流程图如图4所示。

6 改进微粒群算法

PSO算法具有概念简单、易于实现、以及较强的全局收敛能力和鲁棒性等优点,但是它同时也具有智能群体算法的固有缺陷,容易陷入局部最优[7]。在污水处理控制系统优化中常用的改进PSO算法有以下几种。

(1)预筛选机制。首先产生大量的微粒,然后计算各微粒的适应值,并根据适应值的大小对微粒进行排序,从中选出较优的若干微粒,最后对所选较优微粒做进一步的搜索。

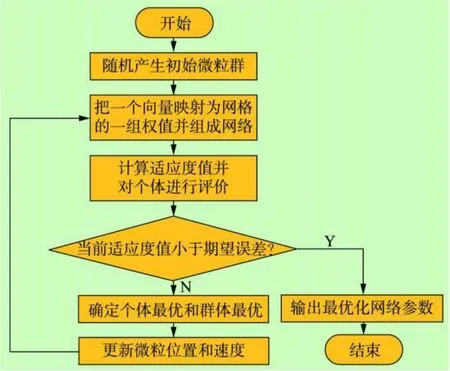
图4 PS O优化BP神经网络程序流程图

(2)分工合作的思想引入到算法中,简单地将微粒分成几个不同的群,分别赋与不同的惯性权重,即给部分微粒赋与较大的惯性权重,这部分微粒主要承担拓展搜索空间、寻找好的区域的任务;同时给部分微粒赋与较小的惯性权重,这部分微粒主要承担在已经搜索到的最优区域里进行局部搜索的工作。这样对微粒进行分群,避免了在代数的增长的过程中调整惯性权重的困难工作,较好地协调了算法的局部与全局搜索能力。

(3)学习因子改进。在粒子群优化算法中,加速系数C1和C2分别控制“认知”部分和“社会”部分对粒子速度的影响。一般来讲,在基于种群的优化方法中,总是希望个体在初始阶段能够在整个寻优空间进行搜索,不至于过早陷入局部值;而在结束阶段能够提高算法收敛速度和精度,有效地寻找到全局最优解。因此,我们可以在进化过程中动态的调整加速系数C1和C2的值,使得在算法的初始阶段,具有大的“认知”部分(C1)和小的“社会”部分(C2),以利于算法在整个寻优空间进行搜索;而在算法后期,应有小的“认知”部分(C1)和大的“社会”部分(C2),更利于算法收敛于全局最优解,提高算法收敛速度和精度。为此,取C1和C2分别如下:

式中Maxiter和iter分别为算法最大叠代次数和当前代数。Cstart和Cend为C2的初始值和最终值,0＜Cend＜Cstart≤4。

(4)惯性惯性权值改进。固定权值的选择就是选择某一常数为惯性权值,在优化过程中不变。然而在实验中的效果并不十分理想,所以开始研究惯性权值w对优化性能的影响,发现较大的w值有利于跳出局部极小点,而较小的 w值有利于算法收敛,提出了一种根据算法叠代次数使惯性权值线性递减的方法。算法在初期使用较大惯性权值,具有较强的全局搜索能力,后期则使用较小惯性权值,提高局部搜索能力。为了找到一种能在全局搜索和局部搜索之间取得最佳平衡的惯性权值选取方法,研究人员进行了大量的研究工作,先后提出了线形递减权值(LDIW)策略[8]、模糊惯性权值(FIW)策略[9]和随机惯性权值(RIW)策略[10]。

惯性权重的函数形式通常为

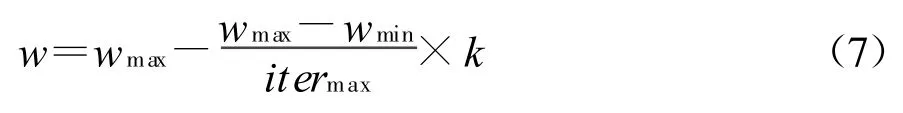
式中,wmax为初始权重;wmin为最终权重;itermax为最大迭代次数;k为当前迭代次数。这个函数使得微粒群算法在刚开始时候倾向于发掘,然后逐渐转向于开拓,从而在局部区域调整解。这些改进使得微粒群算法的性能得到很大的提高。

(5)动态改变最大速度。最大速度决定在当前位置与最优位置之间区域的分辨率。同惯性权重w一样,它也起着平衡全局和局部搜索能力的作用。一般将速度限定值Vmax设置为每维变量的变化范围。如果Vmax太高,微粒可能飞过好解;如果Vmax太小,微粒不能在局部区间之外进行足够的搜索,导致陷入局部优值[11]。

该限制有3个目的:①防止计算溢出;②实现人工学习和态度转变;③决定问题空间搜索的粒度。

在搜索的前期,需要最大速度尽量大,使微粒能够进行全局寻优,而随着迭代的进行,最大速度应该越来越小,使微粒以较小的最大速度进行局部寻优。为了跳出局部最优需要较大的步长,而在接近最优值时,采用更小的步长会更好。设置较大的Vmax可以保证粒子群的全局搜索能力,较小的Vmax则使粒子群的局部搜索能力加强。所以,最大速度Vmax应该按照下式动态减小:

7 结 语

对微粒群优化算法的研究尚处于初期,还有许多问题有待解决。而把微粒群算法应用于污水处理系统中的研究就更少。本文参考大量文献,对微粒群算法在污水处理控制系统中的优化问题进行了总结和论述,但是还有许多工作要做,例如应用哪种控制方法能产生最满意的结果,微粒群算法的哪种改进方法在污水处理系统中能产生最好的效益等还有待进一步研究。本文简要介绍了污水处理中微粒群算法的应用以及污水处理系统中的各种改进微粒群算法,希望对在污水处理中研究微粒群算法的读者有所启发。

[1]李 骏.SBR污水处理工艺的模糊控制[D].上海:上海交通大学2003:1-35.

[2]于广平,张 平,魏松岩,等.仿人智能PID控制及在污水处理溶解氧控制中的应用[J].微计算机信息,2006,22(2-1):13-15.

[3]Kennedy J,Eberhart R.Particle swarm optimization[C]//Pro IEEE Int Conf on Neural Networks.Perth,1995:1942-1948.

[4]邵会锋.改进粒子群算法在PID参数整定中的应用[J].电气传动自动化,2010,32(2):22-24.

[5] 曾建潮,介 婧,崔志华.微粒群算法[M].北京:科学出版社,2004:5.

[6]沈学利,张红岩,张纪锁.改进粒子群算法对BP神经网络的优化[J].计算机系统应用,2010,19(2):57-61.

[7]Eberhart R, Shi Y.A modified particle swarm optimizer[C]//IEEE World Congress on Computational Intellig-ence,1998,69-73.

[8]Shi Y,Eberhart R.Empirical study of particle swarm optimization[C]//International Conference on Evolutionary Computation.Washington,USA:IEEE,1999:1945-1950.

[9]Shi Y,Eberhart R.Fuzzy adapitve swarm optimization[C]//The IEEE Congress on Evolutionary Computation.San.Francisco,USA:IEEE,2001:101-106.

[10]Eberhart R,Shi Y.T racking and optimizing dynamic systems with particle swarms[C]//The IEEE Congersson Evolutionary Computation.San Francisco,USA:IEEE,2001:94-100.

[11] 康 琦,张 燕,汪 镭,等.智能微粒群算法[J].冶金自动化,2005(4):529-532.