全变差图像去噪模型的快速求解

余瑞艳，刘 文

(1．长江大学 一年级教学工作部，湖北 荆州 434020;2．武汉理工大学 理学院，湖北 武汉 430070)

图像复原是数字图像处理中的一个重要分支，它的主要目的是改善图像的质量。由于实际中设备的不完善和物理条件的限制，所获得的图像通常达不到期望的质量［1］，因此，原始图像的复原是非常必要的。目前，在图像复原研究领域中研究者普遍认为图像的边缘是最重要的视觉特征。1992年，RUDIN等提出的全变差正则化(total variation regularization，TVR)模型被认为是目前比较合理的能够保持图像边缘特征的图像模型［2］。有关全变差正则化模型的求解一直是相关学者的研究重点，RUDIN等提出的人工时间演化方法是目前使用最为广泛的求解算法，该类算法用求解TV模型的欧拉－拉格朗日方程来达到图像去噪的目的，但这种解法受到CFL(courantfriedrichs－lewy)条件的限制，尤其在图像的平坦区域该算法的收敛速度很慢。为了消除CFL条件的限制，VOGEL和OMAN提出了一种固定点迭代方案，该方案直接求解稳定的欧拉－拉格朗日方程，但该求解方案仅仅线性收敛［3］。于是CHAN等使用TV模型的双变量描述，进而得到一种具有鲁棒性的求解方法［4］。但上述各种求解算法均存在收敛速度慢的问题。基于此，笔者在研究Bregman 迭代正则化的基础上［5－8］，构建了求解全变差正则化模型的快速迭代算法。

1 全变差正则化模型

令u为原始的清晰信号，u0为被噪声污染的信号，即:

式中，n为具有零均值，方差为σ2的高斯白噪声。

相比于图像复原的逆滤波方法、伪逆方法和最大熵方法，全变差正则化方法在保持图像边缘与平滑噪声问题上具有更好的特性。全变差正则化方法通过引入一定的约束将图像复原转换成适定问题，并能确保图像复原结果的存在性、唯一性，且具有受噪声干扰较小的优点。

RUDIN等研究发现受噪声污染的图像的总变差(如图1所示)明显比无噪图像的总变差大，于是将总变差定义为梯度幅值的积分:

其中:▽xu，▽yu分别为图像u在x和y方向的梯度;Ω为图像u的定义域。限制总变差就会限制噪声，于是将图像的复原问题转化成如下的最小化问题:

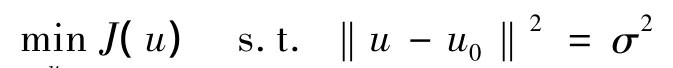
从图1可以看出，全变差最小化能够抑制噪声，但并不对解产生一种平滑作用，这样就有可能使图像的边缘(突变)在最小化全变差过程中被保存。但若以作为平滑性的度量，则对于图1中的3个函数而言，显然有:

图1 全变差的性质

即曲线3将被认为是最平滑的，曲线2次之，曲线1最不平滑。于是在最小化时，大的跳变将最先被平滑。因此在图像复原过程中，全变差能够起到保留图像边缘的作用。

按Lagrange乘子法则，全变差最小复原问题就是求解E(u)的最小化问题muin E(u):

式中，μ为正则化参数。

2 构建快速迭代算法

为了提高图像去噪的效果，笔者将各向同性的全变差图像去噪模型式(2)转化成如下的各向异常全变差图像去噪模型:

定义图像 u:{1，2，…，M}× {1，2，…，N}→IR，即 u∈IRM×N，且

其中，▽xu(i，j)=u(i，j)－ u(i－1，j)，i=2，…，M，j=1，2，…，N;▽yu(i，j)=u(i，j)－ u(i，j－1)，i=1，2，…，M，j=2，…，N。且▽xu(1，j)=0，j=1，2，…，N;▽yu(i，1)=0，i=1，2，…，M。

模型式(3)的求解要研究n维欧式空间IRn中凸泛函的极小化问题。令E:IRn→IR是一凸泛函，定义E在点v∈IRn处的次梯度为g，且:

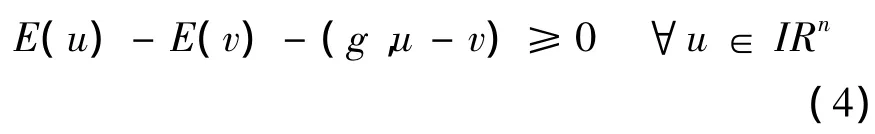
偏导数∂E(v)是E在点v处的次梯度结合。显然，当且仅当0∈∂E(v)时，v是泛函E的极小值点，即:

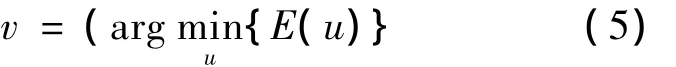
对于 λ ＞0，c∈IR，定义函数 cut如下［9－10］:

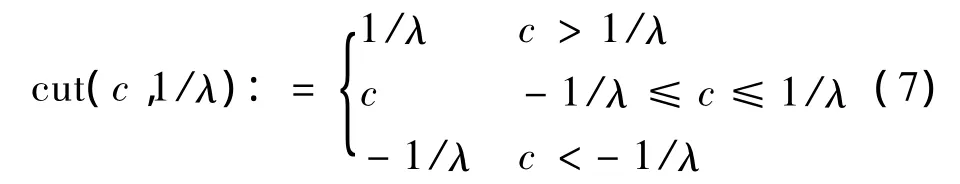
根据式(6)和式(7)，显然有 shrink(c，1/λ)+cut(c，1/λ)=c。对于模型式(3)的求解，令，对于 k=1，2，…，有如下的迭代格式:

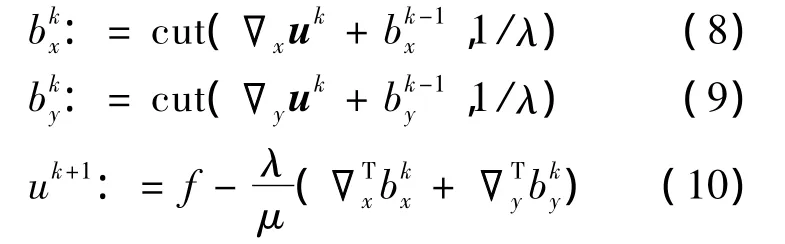
其中:

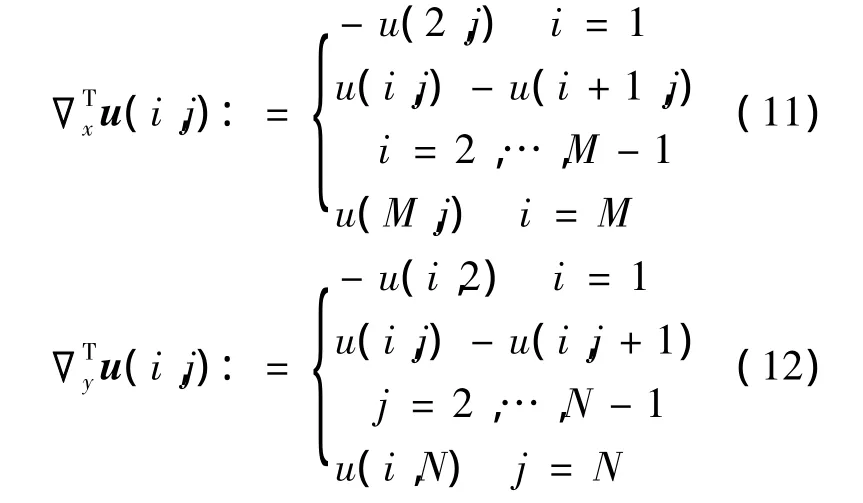
3 实验结果及分析

为了说明快速迭代算法求解全变差去噪模型的有效性，笔者进行了大量的仿真实验，现以Cameraman图像为例进行说明和分析。实验是在CPU Intel(R)2．0 GHz，1 G 内存，Matlab 6．5 环境下运行的。采用峰值信噪比(PSNR)作为客观的衡量标准，PSNR定义为:

式中:u0(i，j)为原始图像;u(i，j)为复原后的图像;M×N为图像大小。

笔者利用基于Bregman迭代正则化方法的算法快速求解全变差图像去噪模型，并与RUDIN人工时间演化方法的图像去噪结果进行比较分析。实验中图像噪声的 PSNR分别为18．640 0 dB、22．123 2 dB 和 28．139 8 dB，式(8)～ 式(10)中的参数分别为 λ=0．001，μ=0．025。图2为降噪处理前后Cameraman图像的视觉效果，表1为3幅图不同算法的降噪效果。

图2 降噪前后的Cameraman图

表1 3幅图不同算法的图像降噪效果

仿真实验结果表明，笔者算法的求解速度远高于人工时间演化方法，含噪模糊图像的降噪效果明显，在去除图像噪声的同时能保留图像的边缘，人眼能直观地感受到图像质量的改善，其峰值信噪比相比于人工时间演化方法有显著的提高。

［1］ JIA R Q，ZHAO H Q．A fast algorithm for the total variation model of image denoising［J］．Adv Comput Math，2010，33(2):231 －241．

［2］ RUDIN L，OSHER S，FATEMI S．Nonlinear total variation based noise removal algorithm［J］．Physica D，1992(60):259－268．

［3］ VOGEL C，OMAN M．Iteration methods for total variation denoising［J］．SIAM J Sci Comput，1996，17(1):227－238．

［4］ 吴斌，吴亚东，张红英．基于变分偏微分方程的图像复原技术［M］．北京:北京大学出版社，2008:153－174．

［5］ GOLDSTEIN T，OSHER S．The split Bregman method for L1regularized problems［R］．UCLA:［s．n．］，2008．

［6］ JIA R Q，ZHAO H Q，ZHAO W．Convergence analysis of the Bregman method for the variational model of image denoising［J］．Appl Comput Harmon Anal，2009(27):367－379．

［7］ OSHER S，BURGER M，GOLDFARB D，et al．An iterative regularization method for total variation－based image restoration［J］．Multiscale Model Simul，2005(4):460－489．

［8］ YIN W T，OSHER S，GOLDFARB D，et al．Bregman iterative algorithms for L1－minimization with applications to compressed sensing［J］．SIAM J Imaging Sci，2008(1):143－168．

［9］ WAN E A，MERWE V D．The unscented kalman filter for nonlinear estimation［C］//In Proceedings of Symposium 2000 on Adaptive Systems for Signal Processing，Communication and Control．Lake Louise，Alberta:AS－SPCC IEEE，2000:635－650．

［10］ RISTIC B，ARULAMPALAM S．Tracking a manoeuvring target using angle－only measurements:algorithms and performance［J］．Elsevier，Singal Processing，2003(83):1223 －1238．