预应力混凝土结构的应变控制分析

吴 迅， 贾留锁， 王艺桥

(同济大学 桥梁工程系，上海 200092)

迄今以来，规范对混凝土力学行为的研究总是集中于应力，通常的状况就是在考虑各种最不利荷载组合状况下，关注应力是否超限。对于单轴受力体系而言，关注的对象是正应力;对于多轴受力体系而言，关注的对象是正应力和主应力。规范的思路就是在考虑一定的安全度的情况下，如果构件最危险截面上正截面正应力不超限，斜截面主应力不超限，则结构就是安全的［1］。

广为熟知的各种强度理论也大多以应力作为判断准则。通过单轴拉伸和压缩的基本试验得到数据，并通过引入一定的假定便可以得到主应力空间上的屈服面和破坏面，通过计算得到实际工程中构件的主应力，如果此主应力空间点在屈服(破坏)面内，我们就认为材料不屈服(破坏)，在屈服(破坏)面上，则材料开始屈服(破坏)，在屈服(破坏)面外，则材料已经屈服(破坏)［2］。

以应力为标准的判断准则在工程中实践了许多年，但实际工程中始终不曾消失的大量裂缝一次又一次刺激着工程师的神经。对比规范可以看到:且不说作用分项系数对于作用效应的放大，以及材料分项系数对于材料抵抗力的缩小，单单在理论状况下，开裂部位的主拉应力值与混凝土的开裂强度也有一定的差距。本不应开裂的部位接二连三地出现裂缝，这不得不让我们深思规范中主应力和正应力不超限判断标准的不足之处。

1 材料强度的微观解释

材料按其内部原子的排列方式，可以分为两大类，即晶体和非晶体。从微观上讲，材料断裂或者裂缝出现的本质解释是外部作用导致分子间引力的丧失。事实上，分子间同时存在着吸引力和排斥力，构成一对矛盾的双方，固体压缩受阻就是斥力在起作用，而拉伸受阻则是吸引力在起作用。分子力是分子间距离r的函数。其关系用图1(a)来表示。

固体在通常情况下，分子都保持在平衡位置r0附近，若分子距离稍大于r0，引力起作用，把分子拉回r0;若分子间距小于r0，斥力起作用，把分子退回r0。如图1(b)所示。但分子力包括吸引力和排斥力都随距离的增大而减小，斥力比引力随距离增大而减小得更快。由此可见，材料断裂的实质就是外部作用导致分子间距大于某一数值，分子间的吸引力不起作用。据此可以得出以下结论:力或者应力是导致材料裂缝的直接原因，其根本原因是分子间距离的增大导致分子引力作用的减弱，即应变才是材料开裂的本质原因。即只要分子间距大于分子引力的影响范围，则材料必然开裂。对于混凝土材料，也有试验证明其破坏发生在极限拉伸变形，而不是发生在极限拉应力时［3］。

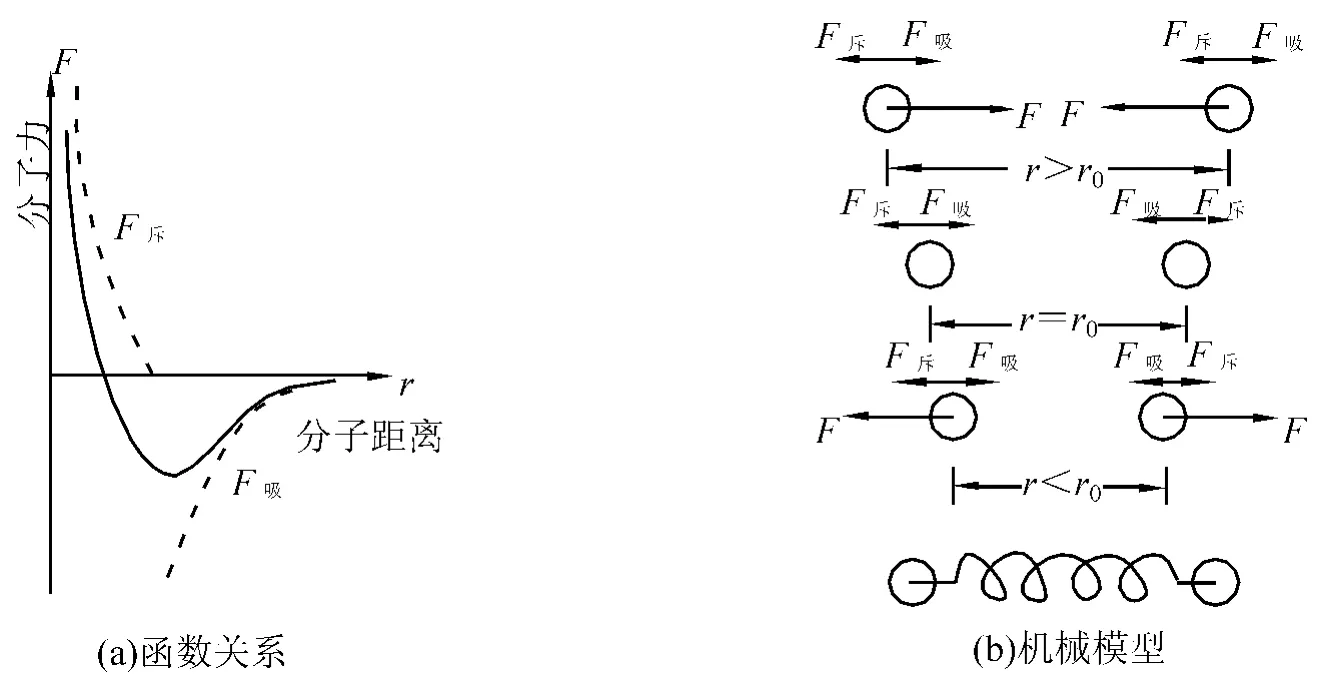
图1 分子力与分子距离的关系

2 应力和应变的失效判别

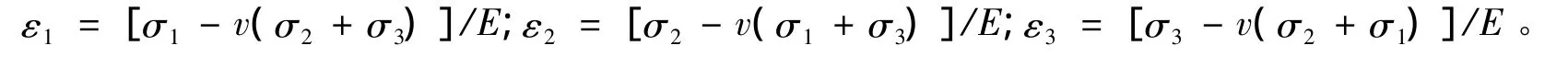
很容易得出如下结论:多维状态下混凝土的三向受压并不意味着混凝土内部无拉应变。即如果微元体各个方向下的压应力差得太多，则混凝土仍可能因拉应变过大而开裂［4］。根据胡克定律:一个方向上的应力导致的应变可以通过泊松比反映到与之方向垂直的应变上，考虑到实际工程中弹性模量Ec不发生变化，则相当于在垂直的不受力方向上施加了Fv的拉力。众所周知，混凝土抗拉强度仅为其抗压强度的十分之一左右，并且随着混凝土强度等级的提高比值越来越小。而泊松比 的取值规范规定是0.2。所以应力不超限而垂直方向应变超限的状况在双向受力差别较大的情况下很容易发生。而现今的规范对于这点并没有做出相应的规定，设计人员做设计时并不会对这方面进行验证，这也在一定程度上导致了裂缝的出现。

在一些桥梁的实际调查中，常有竖向预应力筋永存预应力不到位的情况，甚至在施工完成以后，有的预应力筋内无预应力。同时由于箱梁高度有限，对施工要求高，稍有不慎，竖向预应力可能会损失过半［5］。在此情况下，腹板两个方向受的预压力相差太多，则与主压应力相垂直的方向上很可能会出现超限的拉应变，从而导致腹板裂缝出现。

下面以一工程实例，利用大型有限元分析软件ANSYS来阐述这种现象。模型为一左右双幅预应力混凝土双T连续刚构桥，力学简化模型如图2所示。最大悬臂长80 m，全长160 m，采用直腹板单箱单室结构，箱梁顶面宽度为12 m，箱体宽度为6.5 m，T端部梁高2.5 m，根部梁高4.5 m，其余主梁高度采用2次抛物线变化。箱梁采用C50混凝土，纵向、竖向双向预应力布置。纵向预应力采用顶板束和底板束两种类型，为大吨位群锚体系。顶底板预应力钢束均采用低松弛钢绞线，单根张拉控制力为195.5 kN。竖向预应力采用精轧螺纹粗钢筋，张拉控制力为540 kN。采用实体Solid和杆系Link建模，以初应变模拟预应力，并根据结构对称性，选取纵向以及横向1/2结构建立空间实体单元有限元模型，如图3所示。图4为全桥有限元模型，图5为模型纵、竖预应力筋单元。最后利用面操作命令观看腹板应力、应变状况［6］。

图6、图7分别为竖向预应力损失度为60%时的腹板主应力和主应变图。对比看到，在竖向预应力损失度为60%时，腹板处出现了第一主应力为压应力，即腹板大部分处于三向受压状况，而第一主应变为拉应变的状况。且拉应变数值也大到不能忽略的地步。这充分说明了:三向压应力结构出现不可忽略的拉应变是可能发生的，应力判断标准并不是绝对安全的。

图2 全桥力学计算模式简图

图3 模型纵向、横向简化图

图4 全桥有限元模型

图5 模型纵、竖预应力钢筋单元

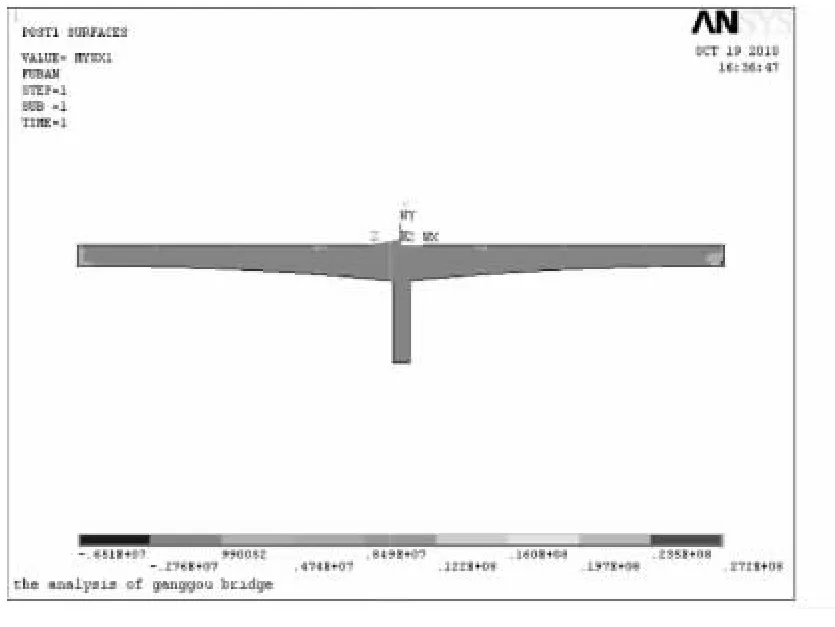
图6 腹板第一主应力图

图7 腹板第一主应变图

3 对现行规范有关混凝土时变条文的讨论

上面讨论了瞬时力学行为下混凝土应力判断标准的不足。在材料的瞬时力学行为中，应力和应变的关系就是一个胡克定律或者广义胡克定律，在各向同性的材料中，主应力和主应变的方向也相同。区别只是在这种情况下，应力判别准则无法考虑其他方向上应力的影响，而应变准则则可以考虑其它方向上应力的影响。另外，对于混凝土这种时变材料，还必须引入混凝土时变特性对于变形的影响。

公路钢筋混凝土及预应力混凝土桥涵设计规范(JTG D62—2004)中对于混凝土的时变效应做了如下考虑:在计算结构体的挠度时，规范考虑到了由时变效应导致的扩大效应，对于超静定结构，规范考虑了由时变效应导致的次内力［1］。不过，这两个规定都没有谈到对应变的影响。挠度的变化通过预设预拱度加以限制，次内力的影响作为永久作用考虑。因为是以应力准则作为控制，所以由时变效应导致的混凝土老化效应弹性模量Ec的减小也没有作出规定。

从现有的混凝土徐变试验资料中看到:在时变效应下，混凝土的抗变形能力同其变形都是时间的函数，都随时间的变化而变化。在单轴应力状况下的试验中，还没见到有关徐变导致的裂缝的报道，这说明其抗变形能力能够一直包络住其随时间增加的变形。但多轴应力状况下，情况如何呢?在惠荣炎、黄兴国、易冰若所编的《混凝土的徐变》一书中提到了多轴徐变的试验数据，但文章仅仅提到了二轴以及三轴压缩徐变，并没有提及到工程中出现的较多的拉压徐变。无疑，这种状况下的徐变和应变发展以及裂缝的出现规律需要更多的试验数据支撑。只有找到各种应力状况下裂缝随徐变的发展规律才能在工程中为应变控制的思路铺下更好的基础。

4 结语

应力标准的实施有着深刻的根源。首先，结构外界条件大都以广义力给出，包括:恒载和活载。现行规范的计算方法也是首先得到应力，再由应力去推导应变。不过随着结构分析的精细化，在设计阶段越来越多的利用大型有限元软件进行设计复核，譬如AYSYS。这类大型有限元软件的理论基础是有限单元法，计算首先得到的是单元体各节点位移。求导后得到应变，应变再乘以弹性矩阵D得到应力。从应变转化到应力的过程中，包含了诸如平面应力和Hooke定律等基本假设［7］，显然应力数值较之应变数值精度将有所降低。一直以来接受的应力分析已经成为习惯。以应力空间表示的强度理论是强度理论的主导，现在已有不少学者得到了应变空间的强度理论。相信随着研究的深入，应变控制的实施必定能为工程带来一系列变革。

［1］中交公路规划设计院.JTG D62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京:人民交通出版社，2004.

［2］过镇海，时旭东.钢筋混凝土原理和分析［M］.北京:清华大学出版社，2003.

［3］惠荣炎，黄国兴，易冰若.混凝土的徐变［M］.北京:中国铁道出版社，1988.

［4］王恒，刘钊.判断混凝土梁桥开裂的应变准则初探［C］//中国公路学会桥梁和结构工程分会2008年全国桥梁学术会议论文集.北京.:人民交通出版社，2008:873-877.

［5］朱汉华，陈孟冲，袁迎捷.预应力混凝土连续箱梁桥裂缝分析与防治［M］.北京:人民交通出版社，2005.

［6］王新敏.ANSYS工程结构数值分析［M］.北京:人民交通出版社，2007.

［7］韦未，李同春，姚纬明.建立在应变空间上的混凝土四参数破坏准则［J］.水利水电科技进展，2004，24(5):27-29.