基于多项式极点配置的ASVG数字控制器设计

刘晓东，黄洪全

(广西大学电气工程学院，广西 南宁 530004)

1 引言

ASVG是柔性交流输电系统的核心装置之一，它通过从电网吸收或向电网注入一定的无功功率，达到有效减小电网传输损耗、稳定电压、提高功率因数、抑制闪变等目的。ASVG作为柔性输电线路的重要装置，通过设计控制特性良好控制器来提高ASVG装置的工作性能是非常有意义的。针对提高ASVG的控制性能，已有很多方法被提出，工程上最常用的是基于电流解耦的双闭环PI调节，还有具有各自特点的新法如变结构控空间矢量控制，它是稳态时和暂态时采用不同的控制律有快的响应速度［2］，非线性鲁棒控制，直流侧电压最优动态分级控制，状态反馈极点配置，空间矢量双滞环控制策略等本文提出了基于多项式极点配置的控制器设计方法，该方法是基于d－q坐标系下建立的数学模型，进行双闭环数字控制器设计，对于ASVG主要是无功电流控制，设计电流内环控制器为二自由度控制器，直接从时域性能指标入手建立闭环特征方程用多项式法进行极点配置，对指令电流和扰动分开控制，具有良好跟踪性能、抗扰性能和较好的鲁棒性，对电压外环直接根据时域参数建立的闭环特征多项式进行极点配置，设定特定的控制律，使系统具有良好的抗扰性能，有效的消除测量误差。实验结果表明根据所提出的方法设计的控制器能够稳定直流侧电压，有效的消除干扰，良好电流跟踪性能。

2 主电路数学模型

ASVG主电路采用传统的电压型逆变桥如图1，通过设定无功电流指令值从电网吸收或者向电网发出无功。

图1 ASVG主电路

建立主电路的开关周期平均模型如式(1):

S为开关状态，上桥臂开S为1，上桥臂关S为0。

通过坐标变换得到d－q坐标系下的数学模型如式(2)。

式中，Sd、Sq为Sa、Sb、Sc经坐标变换得到的 d － q坐标系下的开关矢量。

因为参考轴与空间矢量同步旋转，故电网电压的d－q轴分量和稳定工作状态的ASVG的d、q轴电流分量皆为直流量，所以可对d－q轴电流分别进行控制，实现对指令电流的跟踪。因为选择参考轴时d轴方向选择为电压矢量方向，根据瞬时无功功率理论可知id代表为有功电流iq代表无功电流。

3 ASVG双闭环控制

在稳定工作状态，旋转坐标系下用矢量表示的ASVG数学模型为:

其中urd=Sdudc，urq=Squdc;ud、uq电网电压矢量的d轴和q轴分量。

根据式建立ASVG对象模型框图如图2虚线框所示［1］，分析式(3)可以认为ASVG输出电压矢量由三部分组成，一是电网电压扰动，二是电流状态反馈部分，三是电流控制器输出所控制部分。

将式(4)代入式(3)得

图2 ASVG系统控制框图

由式(4)可知，对电流的控制通过控制电压矢量来urd，urq实现，因而对电流控制通过三部分实现，一是加入电流状态反馈，二是引入电网电压扰动补偿，三是含有电流控制器的内环控制。

对于三相平衡电网，电网电压扰动可认为是常值扰动，加入前馈补偿即可，可把电流状态反馈作为扰动量处理，通过设计具有较强抗扰性能的电流控制器来降低扰动的影响。

通过前馈补偿和电流状态反馈，电流控制的对象可简化为简单的一阶环节如式(5)，控制原理框图如图2所示。

4 电流内环控制器设计

4.1 电流内环二自由度控制器设计

由于直流电压相对与交流电流变化较慢，进行电流调节时，认为直流电压为定值。

控制方法:采用鲁棒高增益反馈控制，即设计二自由度控制系统，控制器设计中采用多项式方法进行极点配置，直接从时域指标入手寻求控制律，对指令信号的响应和扰动的响应分别进行控制，系统输出iid，iiq始终按理想模型响应指令信号，，即使过程动力学特性有所变化，电流也能按照理想模型响应，具有良好的鲁棒性。

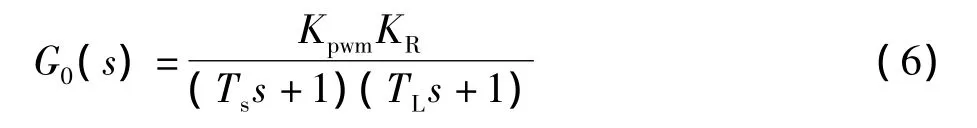
通过双线性变化对式(6)进行离散化［3］得到

离散化以后的极点都为稳定极点，且有一阻尼性良好的极点。

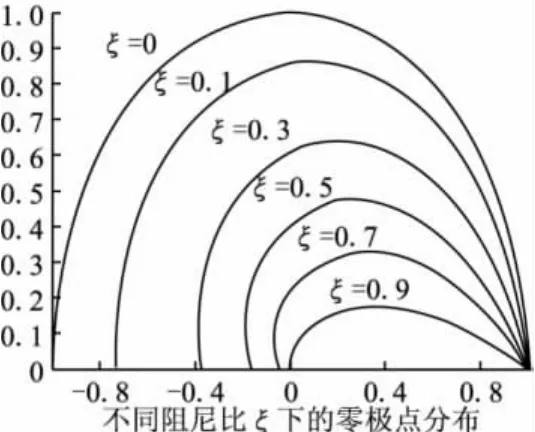
图3 不同阻尼比ξ下零极点分布

图3给出了稳定二阶系统不同阻尼比ξ下零极点分布情况，图中只给出正虚部零极点分布，负虚部零极点分布与正虚部分布关于实轴对称。

根据阻尼比ξ与零极点分布关系的轨迹图确定具有良好阻尼的零点和极点。为了获得较低阶次的控制器，通过分析系统对象式(7)，将阻尼比好的极点z=0作为可消极点。由于系统零点决定输入与输出的耦合关系，可以认为在零点处输入到输出受阻断，因而在式(7)的两个相同零点可用单零点表示，将一个零点z=－1作为可消零点。

令X=X+X－，X+=z－b为阻尼良好的可消部分，X－=z－a;

令Y=Y+Y－，Y+=1，Y－=K0(z+1)2;

式(7)差分方程平移算子表示形式(8)为:

其中q为平移算子。

线性控制律可写为:

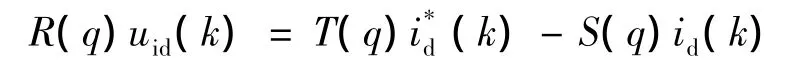
T(z)/R(z)为前馈传递函数，S(z)/R(z)为反馈传递函数;

二自由度控制律平移算子表示形式为:

式(10)决定了系统对指令信号的响应。系统严格按照式(10)理想模型响应指令信号，受系统模型参数影响小，因而具有较好的鲁棒性。

消去过程中可消得零极点后得到系统对扰动响应的闭环特征多项式(10)，

式(10)决定了系统对扰动的响应

图4 电流内环控制原理图

4.2 多项式法进行极点配置

选择满足系统响应要求的闭环传递函数，经过分析与化简将电流内环配置为典型二阶系统:

选择阻尼比ξ=0.707，决定了系统的超调量;根据系统响应要求选择调节时间:

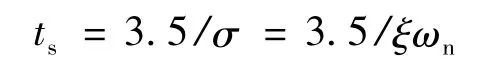
由 ξ和ts选定自然频率 ωn［5］。

二阶系统连续时间到离散时间等价式为［4］:

T为采样周期。

根据式(11)和式(12)得到离散系统响应的闭环传递函数

根据式(10)和式(13)，建立丢番图方程［4］

求解得R－(z)，S－(z)。

令Xm(z)=z2+a1z+a2，Ym(z)=KmY，

根据已经得到的R－(z)，S－(z)，Xm(z)，Ym(z)求得式(9)的控制律。

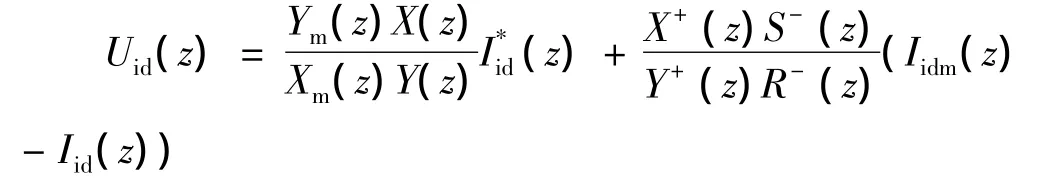
根据式(8)和式(9)求得内环闭环传递函数为:

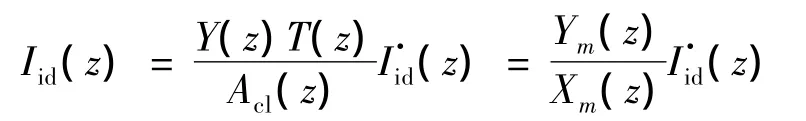
由闭环传递函数可以看出电流内环严格按照理想闭环传递函数响应，即使模型参数有所改变，对系统响应影响较小，系统具有较好的鲁棒性。

应用求iid电流环控制律的方法求得iiq电流环控制律。

加入前馈和电流反馈得到系统电流内环控制率:

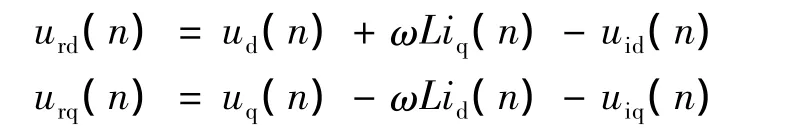
5 电压外环控制器设计

采用多项式极点配置求得电压外环控制律:

电流内环调节速度远快于电压调节速度，稳态时iq跟踪指令无功电流，保持恒定，可作为常值扰动。稳态时Sd为定值，在调节过程中变化范围很小，因而取Sd为定值，假定平衡位置处Sd为m。

采用双线性变换［3］求得:

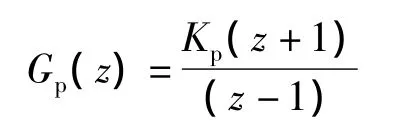
由于电流内环调节速度很快，远远大于电压外环调节速度，在电压变化时，电流已进入稳态，因而可将电流内环简化为比例环节，传递函数为Gil(z)=Kil，电压控制器控制对象为Gp(z)Gil(z)，

求得满足电压环动态响应的闭环传递函数。

设定电压外环构成二阶系统，根据性能指标建立闭环特征多项式Aclu(s)［5］，采用二阶等价连续系统与离散系统等价变换式求得Aclu(z);为保证系统无静差Ru(z)中应含有z－1，减小系统高频测量噪声Su(z)中应含有z+1;

建立丢番图方程

求得Ru(z)，Su(z)，Tu(z)为定态增益常值。

电压环控制律为:

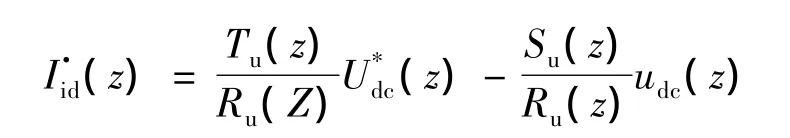
根据式求得电压环闭环传递函数为:

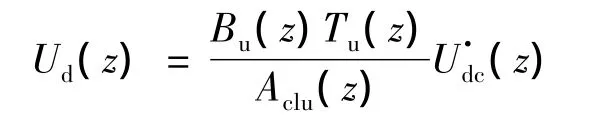
6 仿真和实验结果与分析

通过上述方法设计数字控制器，将设计的控制律在实验设备上进行验证，ASVG实验样机主控TMS320F2812，逆变器主电路输出电感为9.2mH，整流电容为2200μF。开关频率为12.8kHz。

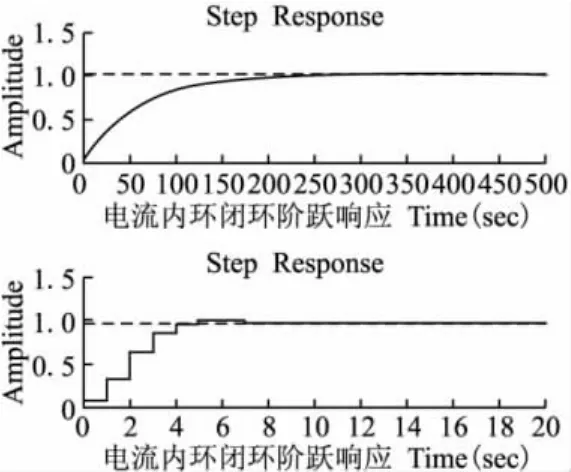
图5 电流环阶跃响应MATLAB仿真图

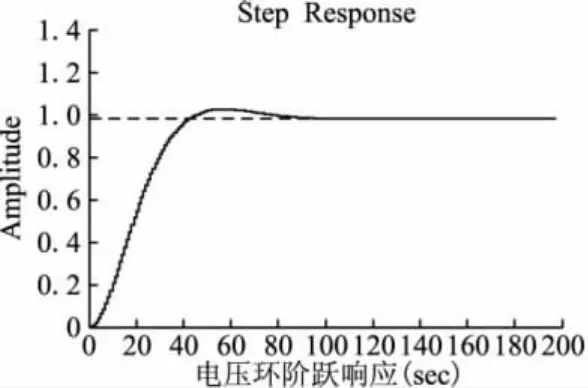
图6 电压外环阶跃响应MATLAB仿真图

由图5可以看出对控制对象未加入控制器时调节时间大于300拍，加入控制器后调节时间为10拍，跟踪速度远远提升，而且超调量小于5%，跟踪时间不超过1ms满足控制要求。图6电压环阶跃响应时间为100拍，响应时间不超过10ms，满足系统要求。图7和图8突然改变负载情况下直流电压波形和输出电流波形，可以看出系统无功电流能够快速跟踪无功指令电流，超调量和调节时间满足系统要求，系统能够快速消除直流电压扰动，确保直流电压的稳定。

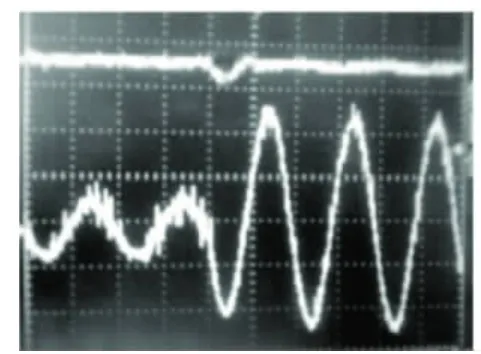
图7 突加负载直流电压和输出电流波形

图8 突加负载直流电压和输出电流波形

图9为a相电网电压和逆变器a相输出电流，在所设计双闭环控制器作用下，ASVG跟踪指令信号向电网发出无功。

图9 a相电网电压与逆变器a相输出电流波形

7 结束语

采用多项式法极点配置的ASVG数字控制器设计方法，进行双闭环数字控制器设计，电流内环控制器为二自由度控制器，对指令电流和电流扰动分开控制，具有良好跟踪性能、抗扰性能和较好的鲁棒性;对电压外环直接根据时域指标建立的理想外环闭环特征多项式用多项式法进行极点配置，设定控制器含特定的环节，使系统具有良好的抗扰性能，确保直流电压的稳定，并且可以有效的减小测量误差。

［1］ 熊健，张凯，陈坚.PWM整流器的控制器工程化设计方法［J］.电工电能新技术，2002，21(3):44 －46.

［2］ 荣飞，罗安.变结构空间矢量控制技术在STATCOM中的应用［J］.电工技术学报，2007，27(12):128 －130.

［3］ 程佩青.数字信号处理教程［M］.北京:清华大学出版社，2001.2，247－251.

［4］ K.J.Astrom，B.Wittenmark(著)，周兆英(译)等.计算机控制系统－原理与设计［M］.北京:电子工业出版社，2001，145－175.

［5］ 胡寿松.自动控制原理［M］.北京:科学出版社，2005，83－108.