涡轴发动机健康管理跟踪滤波器技术
2011-04-27颜秋英时瑞军张秋贵周剑波
颜秋英,时瑞军,张秋贵,周剑波
(中航工业航空动力机械研究所,湖南株洲 412002)
1 引言
航空发动机健康管理技术(EHM),是当前航空发动机控制及故障诊断技术研究的热点之一[1-5],准确辨识航空发动机的健康状态,是其关键。迄今为止,航空发动机的健康状态辨识方法主要包括线性和非线性的气路分析方法(GPA)。使用该方法的关键在于测量参数应当没有噪声。然而测量噪声总是无法消除的,因而线性GPA方法的辨识结果通常是带噪声的数据,无法直接使用,还需要进行滤波处理。非线性的GPA方法由于基于航空发动机部件级数学模型,因而常常因程序不收敛而导致辨识失败[6]。
从20世纪80年代开始,美国利用F-15飞机进行了一系列航空推进系统综合控制技术研究。其中性能寻优控制(PSC)采用跟踪滤波器技术对涡扇发动机的偏差参数进行估计,取得了较好结果[7]。
本文借鉴该方法的基本思想,利用Kalman滤波器原理,建立涡轴发动机的跟踪滤波器,实现了对噪声条件下的发动机健康参数的准确估计,为GPA方法的工程应用提供1个可行的途径。
2 涡轴发动机健康状态
本文研究对象为带自由涡轮的涡轴发动机,主要包括燃气涡轮转子、自由涡轮转子和燃烧室。在磨损、腐蚀、污垢等因素的作用下,涡轴发动机的健康状态会发生变化,反映在压气机和涡轮部件上,即流量和效率的变化;反映在燃烧室部件上,即燃烧室总压损失和燃烧效率的变化。航空发动机部件健康状态的变化,可用所谓的蜕化因子表示[8]
压气机部件的蜕化因子为

涡轮部件的蜕化因子为
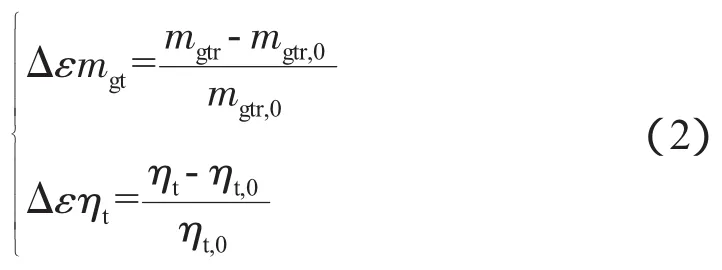
燃烧室部件的蜕化因子为
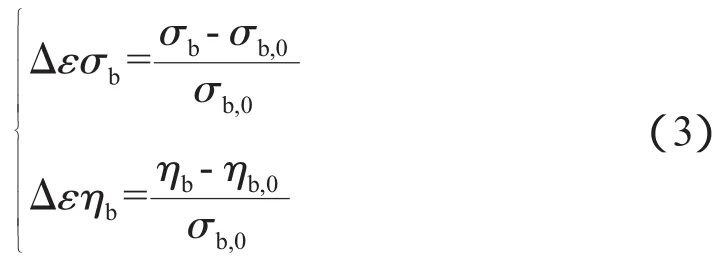
式中:macr、ηc、mgtr、ηt、σb、ηb分别为压气机的换算流量和绝热效率、涡轮的换算流量和绝热效率、燃烧室的总压恢复系数和燃烧效率;下标0表示健康状态变化前的数值。
这样,当发动机某个部件的健康状态发生变化时,通过辨识相应蜕化因子,就能判断出故障的部件及其故障程度;同样,改变部件级模型中部件蜕化因子,就能模拟该部件的故障。
3 涡轴发动机健康状态跟踪滤波器
3.1 线性状态空间数学模型
建立跟踪滤波器,需要建立其线性状态空间数学模型。在众多航空发动机线性状态空间数学模型建模方法中,基于部件级数学模型的建模方法,如抽功法、小偏离方法等应用最广泛。本文采用抽功法,利用涡轴发动机动态数学模型,并根据发动机使用特点,作出适当地调整。修改后的抽功法基本步骤如下。
(1)保持进口条件、燃油流量、导叶角度不变,燃气涡轴上抽功量为0。涡轴发动机数学模型状态稳定后,记录涡轴发动机的燃气涡轮转速ng,0、输出功率Pw0、压气机出口压力P3,0、涡轮间温度T45,0、空气流量mac,0等参数,此为初始状态。
(2)在初始状态下,在燃气涡轴上抽取一定的功率ΔPw;状态稳定后,记录相关数据,之后令ΔPw=0,发动机恢复到初始状态。
(3)在初始状态下,燃油流量变化为Δmf;状态稳定后,记录相关数据;之后令Δmf=0,发动机恢复到初始状态。
(4)在初始状态下,导叶角度变化为Δα;状态稳定后,记录相关数据;之后令Δα=0,发动机恢复到初始状态。
(5)在初始状态下,改变压气机的换算流量蜕化因子 Δεmac,r;状态稳定后,记录相关数据;之后令 Δεmac,r=0,发动机恢复到初始状态。
(6)在初始状态下,改变压气机的绝热效率蜕化因子 Δεηc;状态稳定后,记录相关数据;之后令 Δεηc=0,发动机恢复到初始状态。
(7)采用类似(5)、(6)步骤,可分别得到燃烧室、燃气涡轮、动力涡轮等部件健康状态变化数据。
需要指出的是,由于涡轴发动机在飞行慢车以上状态正常工作时采用恒转速模式,因而在上述过程中,应当调整旋翼总距,使得动力涡轮转速保持不变,以符合涡轴发动机的实际使用情况。
利用以上数据,参考抽功法的基本原理,可建立反映健康状态变化的涡轴发动机线性状态空间数学模型
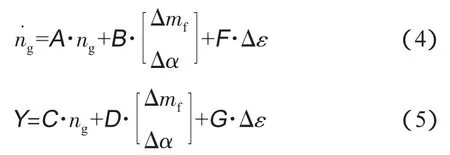
式中:Y 为 ng、Pw、P3、P45、mac以及其他可测参数组成的列向量,Y∈Rn×1;Δε为由蜕化因子组成的列向量,Δε∈Rm;A∈R,B∈R1×2,F∈R1×m,C∈Rn×1,D∈Rn×2,G∈Rn×m。
3.2 测量模型
在发动机实际工作过程中,总是存在各种形式的噪声,同时传感器也有一些噪声,因而实际测量数据总是具有随机性,带有一些噪声,其中最常见的为白噪声。实际测量形式的涡轴发动机线性状态空间模型可表示为
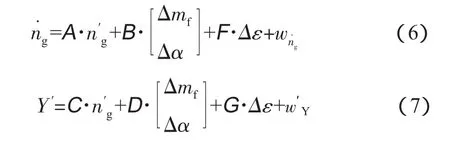
由于航空发动机健康状态的变化相对发动机状态变化而言非常缓慢,因而可认为
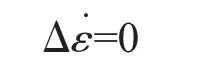
则包含健康状态的实际过程动态方程可表示为m+1维状态空间方程
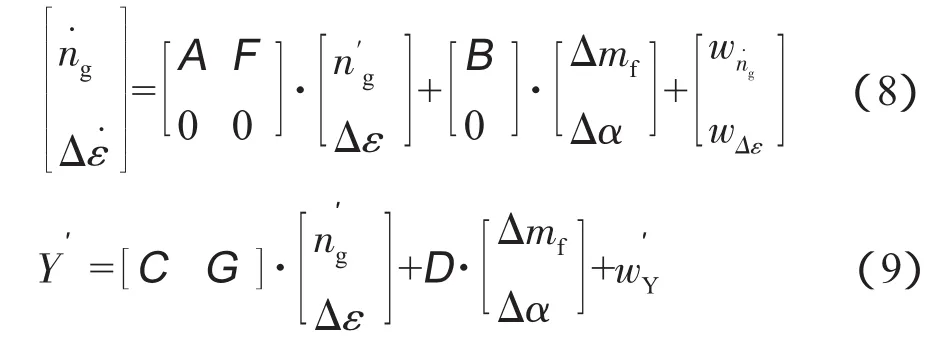
式中:wΔε为蜕化因子向量的测量噪声,wΔε∈Rm×1。
根据线性系统理论,当满足完全可观测条件时,由式(8)、(9)表示的线性系统可通过建立完全状态观测器。即利用输入和输出参数,可观测出系统所有的状态变量。
即当可观测矩阵O满秩时,系统完全可观测
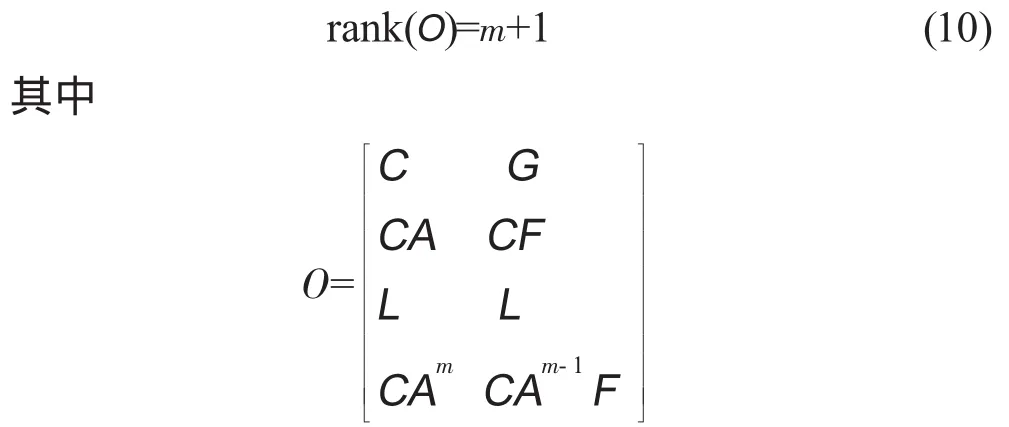
理论分析表明,可观测矩阵矩O满秩的必要条件是
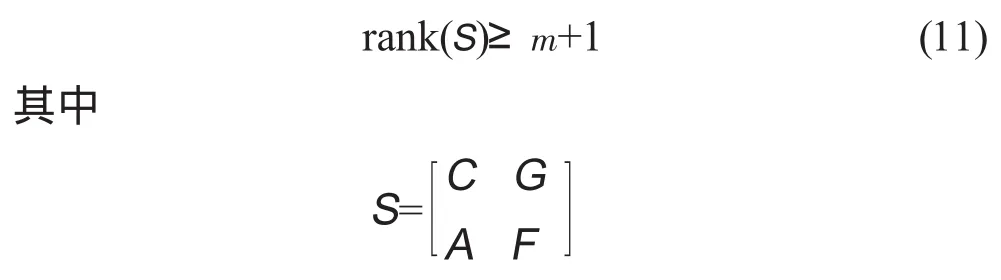
由于矩阵S的秩最大为n+1,因而系统可观测的必要条件是n+1≥m+1,即n≥m。即可测输出参数应不少于待观测状态个数,才可能使系统完全可观测。所以在设计观测器时,选择可测输出参数越多,观测效果越好。
3.3 Kalman滤波器
若式(8)、(9)表示的系统满足可观测条件,则根据Kalman滤波器原理,其完全状态观测器方程为
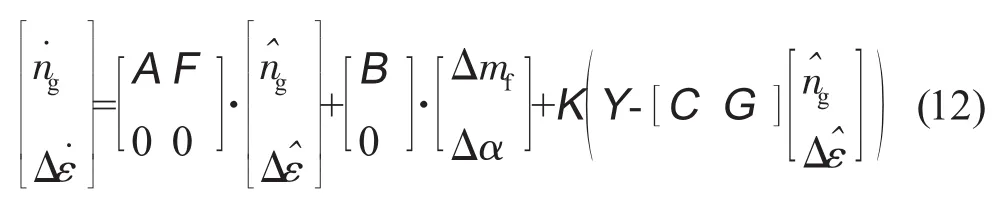
式中:K=PHTR-1,H=[CG],R 为测量输出噪声的协方差阵,即 R=var(w′Y),P 为下面 Riccati方程的解
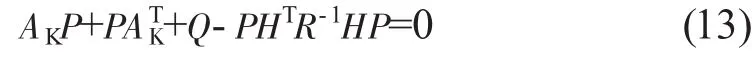
4 仿真结果分析
以压气机健康状态变化为例,对上面建立的涡轴发动机线性状态空间数学模型进行仿真,并与部件级数学模型的稳态结果进行对比;对所建立的健康参数跟踪滤波器进行了仿真研究。
仿真研究的工作点为:PCNC=88.836%,总距为5。选择压气机的健康状态发生变化,即蜕化因子个数为2;选取可测输出参数6个;燃油流量和导叶角度可调,即控制变量为2个。完全保证系统满足可观测条件。
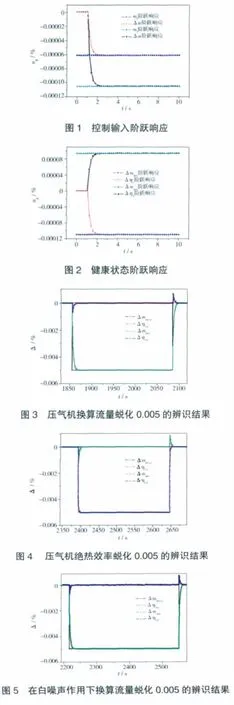
燃油流量阶跃为-0.1%、导叶角度阶跃为0.33%、压气机换算流量蜕化因子、绝热效率蜕化因子分别蜕化0.05%时,线性模型状态计算结果与期望值的对比如图1、2所示。从图中可见,线性模型的计算结果与期望值在不同输入信号下基本吻合,建立的线性状态空间模型具有较高的精度。
在不考虑噪声的情况下,跟踪滤波器在压气机健康状态变化时的仿真效果如图3、4所示。从图中可见,在没有噪声的情况下,滤波器可准确地估计出压气机健康状态的变化。
在白噪声作用下,跟踪滤波器在压气机健康状态变化时的仿真效果如图5、6所示。从图中可见,在白噪声情况下,滤波器仍能准确估计压气机健康状态的变化。
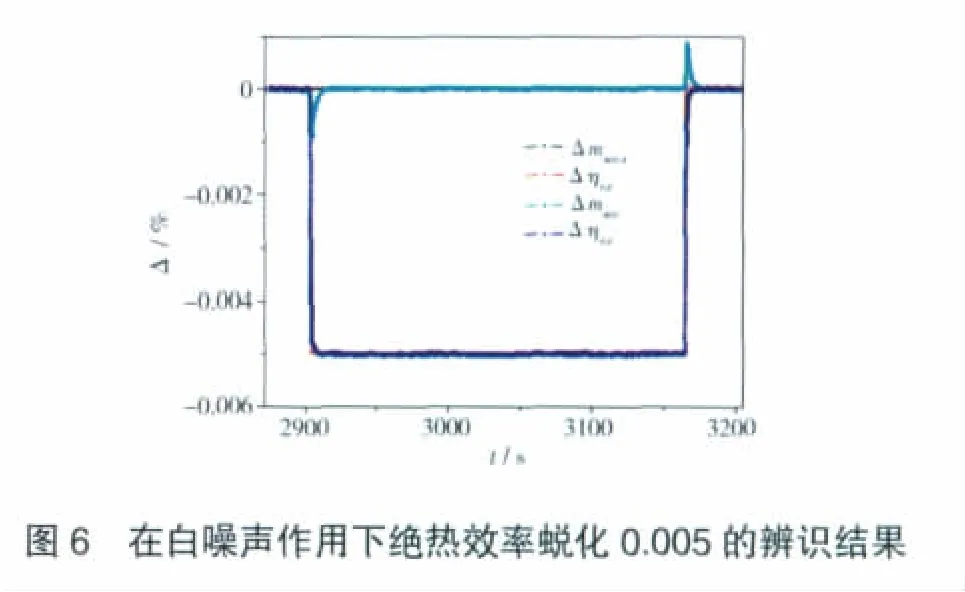
5 结论
以上仿真计算表明,建立的涡轴发动机线性状态空间数学模型具有较高的精度;建立的涡轴发动机跟踪滤波器能够准确估计发动机健康状态的变化,即使存在白色噪声,跟踪滤波器仍能较好地工作。
[1]樊思齐.航空发动机控制[M].西安:西北工业大学出版社,2008.
[2]Sanjay Garg.Controls and Health Management Technologies for Intelligent Aerospace Propulsion Systems [R].AIAA-2004-0949.
[3]D Simon.Aircraft Turbofan Engine Health Estimation Using Constrained Kalman Filtering[R].ASME 2003-GT-38584.
[4]Simon D L,Gang S,Hunter G W,et al.Sensor Needs for Control and Health Management of Intelligent Aircraft Engines[R].ASME 2004-GT-54324.
[5]Simon D L,Garg S,Venti M.Propulsion Control and Health Management(PCHM)Technology for Flight Test on the C-17 T-1 Aircraft[R].NASA-TM-2004-213303.
[6]Li Y G.Gas Turbine Diagnosis Using a Fault Isolation Enhanced GPA[R].ASME 2004-GT-53571.
[7]Espana Martiin D.Torella G,Lombardo G.The Analysis of Influence of Component Performance Decay in Gas Turbines[R].AIAA-95-3031.
