垂直加热通道内超临界水流动稳定性参数敏感性分析

侯 东,许志红,林 萌,刘鹏飞,杨燕华

(上海交通大学核科学与工程学院,上海 200240)

超临界水堆(SCWR)是第四代核反应堆中唯一的压水堆,具有热效率高、系统简单、安装尺寸小和经济性好等众多优点。但是,由于堆芯进出口之间超临界水具有较大的焓差致使其密度发生剧烈变化,并容易引起系统振荡而导致发生不稳定现象。因此,加热通道内超临界水的流动稳定性问题引起了国内外学者的广泛关注[1-8]。

目前国际上主要通过将一维单相流动偏微分控制方程直接进行线性化处理,然后应用频域法在给定的设计参数和工况下对SCWR堆芯进行稳定性分析[2],通过对系统衰减率[2]的计算来考察系统是否稳定。这种方法不具有普适的通用性,只能对特定的系统参数给出稳定性判定。而本文则主要是从超临界压力下水的热工水力学特性本身出发,对垂直加热通道内超临界水流动稳定性机理进行研究,从而得出广泛适用的稳定性判断准则,为后续相关的SCWR设计提供指导。本文将无量纲分析法和频域分析法相结合,定义了影响系统稳定性的关键参数,并给出了各种不同参数所对应的稳定性边界。同时,所提出的无量纲频域分析方法也可为广大科研工作者提供参考。

1 无量纲频域法稳定性分析方法

国际上现在主要存在两大类超临界流动分析方法：一类是将超临界流体流动看作是类似汽液两相流,具体的两相分界点在不同的文献中有不同的定义[2,4];另一类是将超临界流动看作是单相流动,但在流动过程中物性变化比较剧烈。目前国际上没有统一的将超临界流体划分成两相的标准,同时两相流模型中通常需要对流体物性进行简化处理[2],使得分析结论具有很大的不确定度。虽然采用单相流模型不能很好的处理系统压力跨流体临界压力时的相变问题,但是本文的重点是研究大于临界压力的系统稳定性,因此可以不用考虑系统压力降低到临界压力下时的相变情况。同时,相对于两相流模型,单相流模型具有形式简单的优点,不需要对流体物性进行特殊简化,能更准确的描述超临界流体的流动。因此本文采用单相流动模型来分析超临界流体的流动。

现有的公开文献中大都只对无量纲分析方法进行基本阐述,而未给出具体的实现方法。本文将给出无量纲分析与频域法分析相结合的分析方法的具体实施步骤,以为广大科研工作者提供借鉴。

1.1 控制方程的无量纲化

进行无量纲分析的第一步是将原始偏微分控制方程进行无量纲化。管内一维单相流动控制方程(质量守恒方程、动量守恒方程、能量守恒方程)分别为：

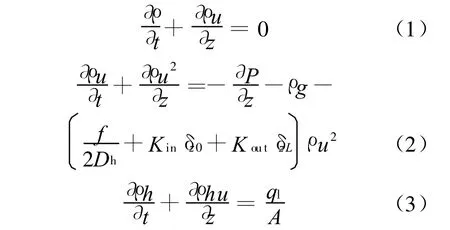
式中：ql是平均线功率;δz0和 δzL分别在z=0和z=L的时候为1,z为其他值时为0;Dh为管道水力直径;f为管道壁面摩擦因数;Kin和Kout分别为管道进出口阻力因数;A为管道流通面积;t表示时间;z表示空间位置;其他参数与常规热工水力参数意义相同。

定义如下无量纲数[4]：

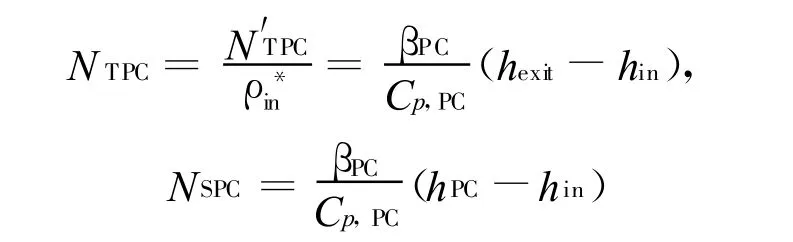
式中 ：ρPC、hPC、Cp,PC和 βPC分别表示给定系统压力下的拟临界温度点的流体密度、焓、定压比热容和热膨胀系数;μin表示入口流体流速;Fr为Frout数;其他参数与常规热工水力参数意义相同。

将各无量纲数代入方程(1)～(3)中,可得无量纲一维流动控制方程。无量纲质量守恒方程：

无量纲动量守恒方程：

无量纲能量守恒方程：

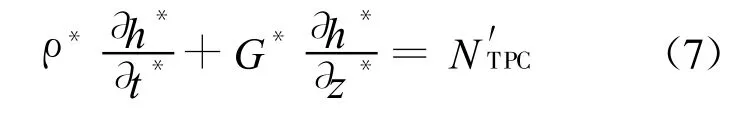
其中无量纲参数NSPC和NTPC是两个重要的确定系统稳定性的参数。从它们的定义可知NSPC主要表征系统入口流体的无量纲过冷度,即系统的入口流体状态;而NTPC主要表征了流体经过系统加热后的体积膨胀率,因此某些文献中[2]将其称为流体膨胀数。系统稳定性边界是由这两个参数组成的点集构成[5]。

经上述无量纲化后,无量纲密度可近似成无量纲焓的单值函数,即无量纲状态方程可表示为[4]：

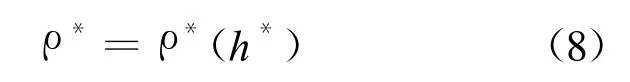
以压力分别为 24.5 MPa、25.0 MPa和30.0 MPa时的无量纲密度和无量纲焓为例,如图1所示,三条曲线完全重合。从国外学者的研究文献中可以发现,包括其他非水工质(如CO2等)在内的各种流体的无量纲密度和无量纲焓的关系曲线也是基本重合的[5]。因此,上述无量纲化处理具有广泛的适用性。

将方程(4)代入到方程(6)中可得：

图1 无量纲密度随无量纲焓的变化Fig.1 Dimensionless density vs.dimensionless enthalpy

方程(5)、(6)或(7)、(9)和状态方程(8)一起构成无量纲控制方程。

1.2 无量纲方程的线性化

为消除空间微分算符,需要对无量纲控制方程进行空间离散,本文在轴向上进行均匀划分网格,采用有限控制体积法进行离散。其中质量与能量方程的控制体是重合的,而动量方程是按照交错网格的方式进行离散化的,其控制体相对质量和能量方程的控制体偏移半个控制体积。空间离散方程如下：

将状态方程代入到质量方程中,可得

上述扰动方程组中各扰动系数由稳态计算值所确定。

1.3 系统特征方程

将线性扰动方程(13)～(15)表示成如下矩阵形式为：

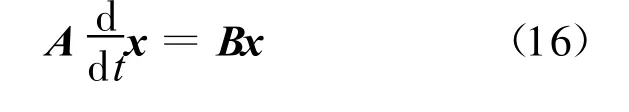
式中：

A和B分别为线性扰动方程的时间导数项系数矩阵和空间离散项系数矩阵。根据频域法的理论[2,6-7],对式(16)时间导数项进行 Lap lace变换可得：

系统的特征方程为：

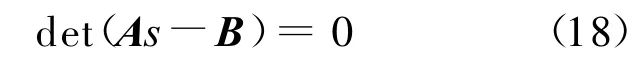
该方程实部最大的根为系统的主特征根λRe+iλIm,根据其实部 λRe便可确定系统的稳定状态。根据频域法理论可知,当λRe＞0时系统是非稳定的,当λRe＜0时系统是稳定的,而当λRe=0时系统处于临界稳定状态。

从系统特征方程(18)可以看出,在计算矩阵的行列式时矩阵中含有非数值元素s,因此不能用常规的数值求解方法来求解式(18)。本文是利用M ATLAB软件提供的符号运算功能[10]来进行特征方程的建立和求解的。

1.4 系统稳态计算

从上述系统特征方程的推导可知,确定系统的稳定边界前必须先确定系统的稳态参数,然后才能求出系统主特征根并确定系统的稳定性[6-8]。

在稳态情况下,所有无量纲方程的时间导数项均为0,根据空间离散方程(10)～(12)有：

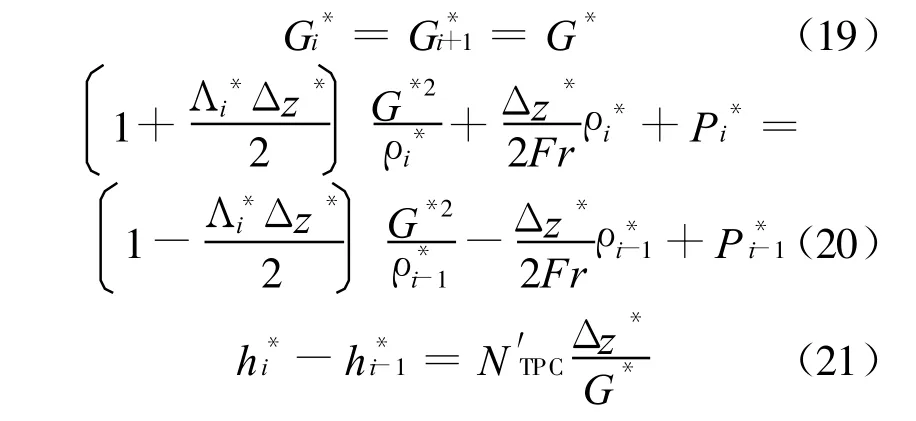
式中：G*为NSPC所确定,各节块h*也能根据能量方程(21)确定,进而ρ*也可以由状态方程(8)确定。根据动量方程(20)可求得进出口压差为Fr的函数,可表示成如下形式：

式中：a和b是根据方程(20)计算得到的常数。

由于本文考查的是流动稳定性中较为重要的密度波稳定性,所计算的问题中进出口压差是给定的常数,即 ΔP*为常数,因此可根据方程(22)可以确定Fr值,进而可以求出系统特征方程的系数矩阵。

1.5 稳定性边界计算

当稳态参数分布确定后,扰动方程的系数矩阵便可以确定,从而系统的特征方程也可确定。在给定NSPC时,通过改变NTPC的值使主特征根的最大实部为 0,由此得到的点(NSPC,NTPC)为一个稳定边界点。所考察范围内的所有边界点一起组成一条稳定边界线,由此可以得到系统的稳定边界。

2 稳定边界的参数敏感性分析

本文所计算问题的系统压力为25MPa,因为目前国内外所设计的SCWR系统压力均为25 MPa。其他相关基本参数如表1所示。

其中,重力加速度g为负数是因为本文主要考虑向下流动加热管道内的流动稳定性,当流体向上流动时g应为正数。

本文通过对不同的系统进口阻力因数Kin、出口阻力因数Kout、摩擦因数 Λ、进出口压差ΔP的稳定性边界计算来观察各参数对超临界流体流动的稳定性影响。上海交通大学设计的混合能谱SCWR堆芯内流体是在下降加热通道中被加热到拟临界温度以上的[9],因此本文主要考虑垂直向下流动的情况,但也同时与流动方向向上时的系统稳定性边界进行了对比。

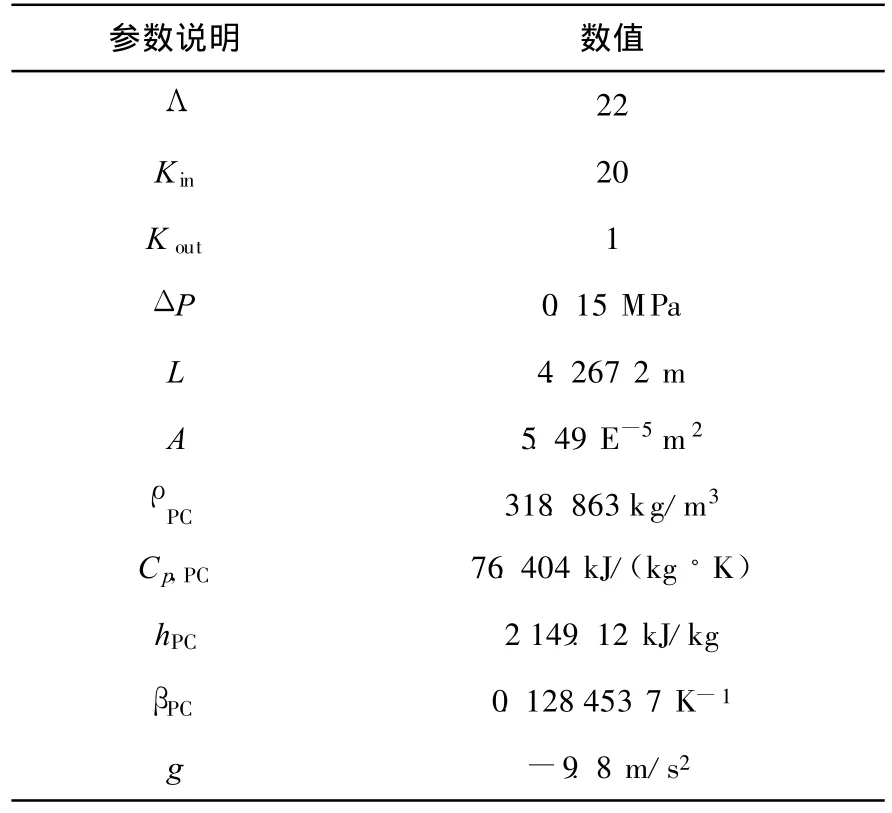
表1 稳定性分析系统参数Table1 Stability analysis system parameters

2.1 入口阻力因数的影响

计算了入口阻力因数分别为0和20时的系统稳定性边界,不同入口阻力系数下的稳定性边界如图2所示。高的入口阻力因数有利于系统的稳定。

图2 不同入口阻力因数下的稳定性边界Fig.2 The stability boundary at different inlet orifice coefficient

2.2 出口阻力因数的影响

计算了出口阻力因数分别为1和20时的系统稳定性边界,不同出口边界阻力因数下的稳定性边界如图3所示。高的出口阻力因数不利于系统的稳定。

图3 不同出口阻力因数下的稳定性边界Fig.3 The stability boundary at different outlet orifice coefficient

2.3 摩擦因数的影响

计算了无量纲摩擦因数分别为5和22时的系统稳定性边界,不同摩擦因数下的稳定性边界如图4所示。高的摩擦因数不利于系统的稳定。

图4 不同摩擦因数下的稳定性边界Fig.4 The stability boundary at different friction coefficient

2.4 进出口压差的影响

计算了系统压差分别为 0.15 MPa和0.25 MPa时的系统稳定性边界,不同进出口压差下的稳定性边界如图5所示。系统进出口压差对系统的稳定性影响较小。

图5 不同系统压差下的稳定性边界Fig.5 The stability boundary at different system pressure drop

2.5 流动方向的影响

计算了垂直向上和垂直向下流动的稳定性边界,如图6所示。流体向上流动比向下流动更有利于系统的稳定。

图6 流动稳定性边界Fig.6 Flow stability boundary

以上稳定性边界计算分析可以对系统的稳定性进行初步判断,为SCWR的堆芯和系统设计提供指导。

3 结论

(1)给出了将无量纲分析与频域法分析相结合来确定系统稳定性边界的详细描述,包括方法论和具体的实施步骤。

(2)通过对加热通道内超临界流体流动方程进行无量纲化、线性化,以及Lap lace变换处理,定义了超临界流动的两个重要无量纲参数NSPC和NTPC,并以此画出了系统稳定边界图。

(3)对系统入口阻力因数、出口阻力因数、摩擦因数、进出口压降,以及流动方向等进行了稳定敏感性分析,为SCWR的堆芯和系统设计提供了指导。

本文下一步的工作将进行SCWR堆芯稳定性分析,并考虑功率反馈下的堆芯响应,以期得到更系统化的稳定性分析结论。

[1] 薛爱军,程旭.超临界水热力系统的稳定性的简化模型分析[J].核动力工程,2009,30(5)：35-38.

[2] Zhao J Y.Stability Analysis of Supercritical Water cooled Reactors[D].Departmen t of Nuclear Science and Engineering,M IT,Camb ridge,Massachusetts,2005.

[3] Lahey R T,Moody F J.The thermal-hydraulics of a boiling w ater reactor[J].American Nuclea Society,1993.

[4] Amb rosiniW.On the Analogies in the Dynamic Behavior of H eated Channels with Boiling and Supercritical Fluids[J].Nu clear Engineering and Design,2007,237：1 164-1 174.

[5] Amb rosiniW,Sharabi M B.Assessment of stability maps fo r heated channelds with supercritical fluids versus the p redictions of a system code[J].Nuclear Engineering and Design,2007,39：627-635.

[6] Chatoorgoon V,Voodi A,Fraaser D.The Stability Boundary fo r Supercritical Flow in Natu ral Convection Loops Part 1：H 20 Studies[J].Nuc lear Engineering and Design,2005,235：2 570-2 580.

[7] A rgonne National Laboratory.Initial Imp lementation of Multi-Channel Therm al-H ydrau lics Capability in Frequen cy Domain SCWRStability Analy sis Code SCWRSA[Z].2005.

[8] Cheng X,Yang Y H.A Point-Hydraulic Model for Flow Stability Analy sis[J].Nuc lear Engineering and Design.2007,238：188-199.

[9] Liu X J,Cheng X.Thermal-hydrau lic and neu tronphysical characteristics of a new SCWR fuel assem bly[J].Annalsof Nu clear Energy,2009,36：28-36.

[10]The MathW orks Inc.M ATLAB Symbolic Math Toolbox 5.4[M].USA：The MathW orks Inc.,2000.