基于单神经元自适应PI的PWM整流器控制

李 梅 李 岚

（太原理工大学计算机与软件学院，太原 030024）

三相PWM整流器具有输入功率因数可调及能量可以双向流动等优点，已被广泛应用于无功补偿、有源电力滤波、高压直流输电及太阳能、风能等可再生能源的并网发电等控制中，通常的三相PWM整流器控制方法是采用基于系统精确数学模型的电网电压定向矢量控制。由于三相PWM 整流器本身是一个强耦合、非线性系统，很难求出其精确的数学模型，为了进一步提高系统的性能，将不依赖系统精确数学模型的智能控制技术引入到三相PWM整流器控制系统，这是目前三相电压型PWM整流器系统的发展方向之一[1-2]。

本文根据三相电压型PWM整流器的基本结构及PWM整流器的数学模型，推出以电网电压定向的矢量控制方法，在Matlab环境下搭建了三相PWM整流器控制系统仿真模型。将单神经元自适应PI控制算法引入到矢量控制系统电压环中，用S函数实现了单神经元自适应PI控制算法，对基于单神经元自适应PI控制算法的系统进行了仿真，结果表明，系统能满足三相PWM整流器控制要求；与基于普通PI控制算法的系统仿真结果进行了比较，证明基于单神经元自适应PI控制算法的系统具有较好的动态跟随性和抗扰性。

1 三相电压型PWM整流器控制方法

三相电压型 PWM整流器的主电路结构如图1所示，包括三相交流电压源、交流侧滤波电感、全控开关器件和直流侧电解电容。

图1 三相电压型PWM整流器主电路

针对数学模型的推导，通常作如下假设[3]：

1）三相电网电压为理想电压源；

2）交流侧电感为线性且不考虑饱和的影响；

3）功率开关管的损耗以理想电阻来表示；

4）为描述能量的双向传输，负载可用有源负载。

1.1 三相静止坐标系下的数学模型

在理想情况下，根据基尔霍夫定律可得三相电压型PWM整流器的微分方程

1.2 同步旋转坐标系下的数学模型

将三相静止坐标系下的数学模型变换到以电网基波频率同步旋转的d,q坐标系下，可以得到电压型PWM整流器在d,q坐标系下的数学模型

根据 PWM 整流器在同步旋转(d,q)坐标系下的数学模型，式（2）中的输入电流满足下式

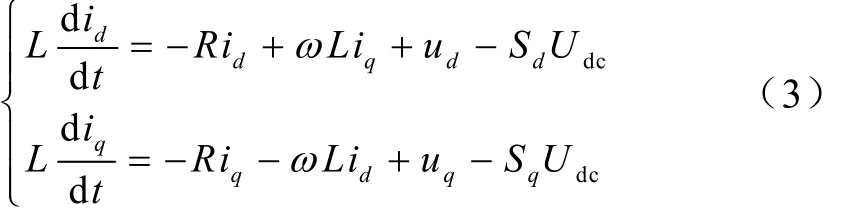
设PWM整流器交流侧电压

则式（3）可写为

因此得三相PWM整流器双闭环控制系统，如图2所示。其中，电压外环的作用主要是控制三相PWM

图2 三相PWM整流器双闭环控制系统

整流器直流侧电压，而电流内环的作用主要是按电压外环输出的电流指令进行电流控制，以实现单位功率因数正弦波电流控制。为简化控制算法，采用电网电压定向矢量控制。

2 单神经元自适应PI控制器的构成及学习算法

单神经元自适应PI控制器的结构如图3所示。

图3 单神经元自适应PI控制器

单神经元自适应控制器通过对加权系数的调整来实现自适应、自组织功能，而加权系数的调整采用有监督的Hebb学习规则，它与神经元的输入、输出和输出偏差三者的相关函数有关，即

式中，z (k)为输出误差信号，z(k)=yr(k)-y(k)；η为学习速率，0η＞；c为常数，0c＞。

为保证上述单神经元自适应PI控制学习算法式（11）的收敛性和鲁棒性，对上述学习算法进行规范化处理后有

对比例（P）、积分（I）可以分别采用不同的学习速率ηP，ηI以便对它们各自的权系数能根据需要分别进行调整，其取值由仿真与实验确定。

3 三相PWM整流器控制系统建模

将基于单神经元自适应PI控制器取代图2所示系统电压环的常规PI控制器，利用 Matlab软件中Simulink模块搭建基于单神经元 PI控制器的三相PWM整流器控制系统。

3.1 神经元自适应PI控制器仿真模型的建立

由于单神经元自适应PI控制器不能直接用传递函数加以描述，若简单地应用Simulink将无法对其进行仿真，在此引入了S函数。

S函数所包含的信息可用以下调用格式进行查看

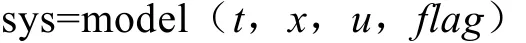
其中，t、x、u为当前时间、状态向量与输入向量；flag为返回变量标志，控制返回变量的信息。

基于有监督的Hebb学习规则[4]的神经元PI控制器的S函数为

编写S函数后，就可以建立其Simulink仿真模型，其步骤是：①输入函数变量名及参数变量名。单击Simulink模型库中非线性环（Nonlinear）的S-Function模块，并拖动到所打开的模型窗口上，双击S-Function模块，按照相关的提示输入函数变量名和参数变量名；②创建子系统（Create subsystem）；③屏蔽子系统（Mask subsystem）。在屏蔽子系统的对话框中按照提示输入参数变量。当该模块被屏蔽后，双击该模块就会出现参数输入对话框，双击该模块，同样也可以对输入参数进行修改。单神经元PI控制器模型如图4所示。

图4 单神经元自适应PI仿真模型

3.2 三相PWM整流器系统仿真模型的建立

根据图2所示三相PWM整流器控制系统工作原理，建立基于单神经元自适应PI控制器的整流器控制系统仿真模型，如图5所示。

图5 三相PWM整流器系统仿真模型

其仿真参数为：输入相电压的峰值U= 1 00V；滤波电感L= 7 mH；输入等效电阻R= 0 .3Ω；直流侧电容C= 4 700μF；PWM开关频率为10kHz。

4 仿真结果

基于仿真模型，设定仿真时间为2s，对三相PWM整流器整流工作状态、逆变工作状态及工作状态转换进行了仿真。

当直流侧电压给定 Udc∗取270V、交流侧q轴电流给定iq∗取0A，纯电阻负载，t=0.5s时直流电压给定由270V变为320V；t=1.0s时负载发生突变（由30Ω变为22.5Ω）；t=1.5s时，负载由纯电阻性质变为反电势性质（反电势值设定为500V），三相PWM整流器系统交流侧相电压、相电流仿真结果如图6所示，其交流侧相电流有功分量和无功分量仿真结果如图7所示，直流电压仿真结果如图8（实线）所示。

图6 相电压、相电流仿真波形

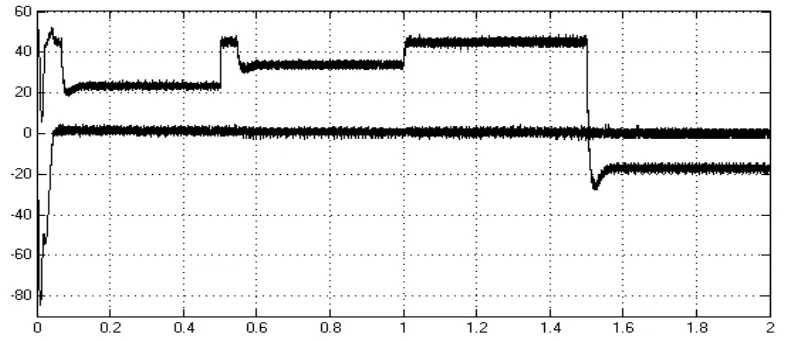
图7 电流有功分量和无功分量仿真波形

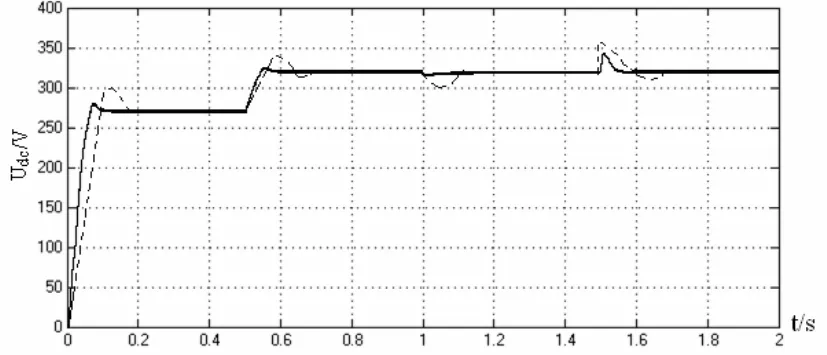
图8 直流电压仿真波形

根据仿真结果，可以得出如下结论：

1）三相PWM整流器在整流工作状态时，相电压、电流相位相同。且当直流电压给定或电阻性负载突变时，电流有功分量能很好地跟随直流电压给定或负载的变化而变化。

2）当三相PWM整流器整流状态向逆变状态切换时，经过很短时间的调节后，相电压、电流由相位相同变为相位相反，整流器由单位功率因数整流状态转换为单位功率因数逆变状态，系统顺利实现了能量的双向流动。

3）与常规的PI控制器相比较（特性如图8虚线所示），基于单神经元PI控制器的三相PWM整流器系统超调量较小，快速性及跟随性较好。

5 结论

神经网络经过学习训练后，能够体现复杂的映射关系，其输入、输出之间的非线性关系隐含在网络本身，这样可以避免求数学模型的困难。三相PWM 整流器本身属于非线性系统，且对系统控制的实时性要求较高。将单神经元神经网络PI自适应控制运用于三相 PWM整流器控制系统，充分发挥神经网络自学习和自适应能力，仿真结果表明，基于单神经元PI自适应的三相PWM整流器控制系统算法能够适应环境的变化、有较强的鲁棒性及动态性能，不需要对被控对象进行精确的辨识，是提高三相PWM整流器控制精度的一种有效方法。

[1] JOSE R Espinoza,GEZA Joos,LUIS Moron.Decoupled control of the active and reactive power in three phase rectifiers based on non-linear control strategies[J].IEEE Trans on Indus Electronics,1999,1:131-136.

[2] 周美娇.单神经元自适应控制理论的研究[D].哈尔滨：哈尔滨理工大学,2002.

[3] 公丕柱.双馈异步风力发电系统网侧PWM整流器的研究[D].太原:太原理工大学,2009.

[4] 李国勇.智能控制及其Matlab实现[M].北京：电子工业出版社,2006.