时频分布的分辨率比较

苏 峰,曲长文,简 涛

（海军航空工程学院,烟台 264001）

0 引 言

信号的时频分布将时域和频域有机地结合在一起,反映信号在时频平面的特征。时频分析通过将信号的时域或频域表示变换为时频二维表示,分析信号的瞬时频谱或频谱随时间的变化规律,是分析非平稳或时变信号的有力工具。线性时频分析方法有短时傅里叶变换、Gabor变换、小波变换等；能量或平方时频分析方法有Wigner-Ville分布、Cohen类分布、模糊函数、谱图、尺度图等。时频分析近几年得到迅速发展,广泛应用到许多领域的信号分析与处理中。

各种时频分布之间有着一定的联系,Cohen类分布是Wigner-Ville分布的一般平滑型,谱图、尺度图是Wigner-Ville分布的特殊平滑型。短时傅里叶变换、小波变换、Wigner-Ville分布是3种典型的时频分布,其它时频分布的性能介于它们的性能之间。短时傅里叶变换、小波变换、Wigner-Ville分布的计算量基本相同。将信号转换为解析信号,Wigner-Ville分布与离散的短时傅里叶变换、小波变换具有相同的频率周期。短时傅里叶变换、小波变换、Wigner-Ville分布的交叉项、分辨率有较大的差别,而交叉项、分辨率是影响它们应用的重要因素。本文主要分析、比较短时傅里叶变换、小波变换、谱图、尺度图以及Wigner-Ville分布的分辨率以及交叉项对分辨率的影响。

1 时频分布

短时傅里叶变换和Gabor变换的基本原理是一致的,均是加窗傅里叶变换。窗函数使短时傅里叶变换具有了局域特性,窗函数的移动使短时傅里叶变换又具有全局特性。短时傅里叶变换是时间和频率的二元函数。信号z（t）的短时傅里叶变换为:

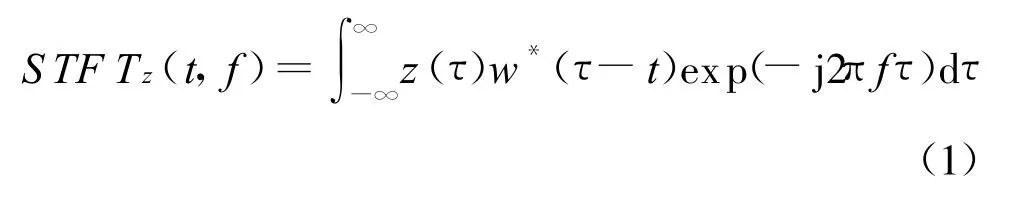
式中:w（t）为窗函数,可以在L2（R）空间内任意选择,一般以具有好的时频聚集性为原则。

短时傅里叶变换是线性的,其模的平方定义为信号z（t）的谱图。谱图是能量时频分布,不满足线性叠加原理。

Wigner-Ville分布是一种能量时频表示,几乎满足期望具有的所有数学性质。信号z（t）的Wigner-Ville分布定义为:

小波变换是一种多分辨分析,其定义为:

当时间平移参数b变化时,窗函数在时间轴上平移。当尺度参数a变化时,窗函数宽度在时间轴上伸缩。若a＞1,使窗函数时宽增大,而窗函数频宽缩小；若a＜1,使窗函数时宽缩小,而函数频宽增大。小波变换是线性变换,其模的平方定义为信号z（t）的尺度图。尺度图是能量时间-尺度分布。

由于小波变换、尺度图是时间-尺度分布,不方便与其它时频表示比较性能。根据小波变换的原理,提出改进小波变换,如下:

当f=0时,改进小波变换变为小波变换；当a=1时,改进小波变换变为短时傅里叶变换。在考虑小波变换的时频特性时,将尺度参数a看作参变量。改进小波变换的模的平方定义为改进尺度图。

2 分辨率分析与比较

时频分布的分辨率是指将时频平面上2个信号区分开来的能力,包括2个参量:时间分辨率和频率分辨率。由于高斯函数满足不确定性原理的最低限,在时频平面上具有较好的聚集性,选择高斯函数作为比较时频分布分辨率的信号。

设高斯信号为:

相应的Wigner-Ville分布为:

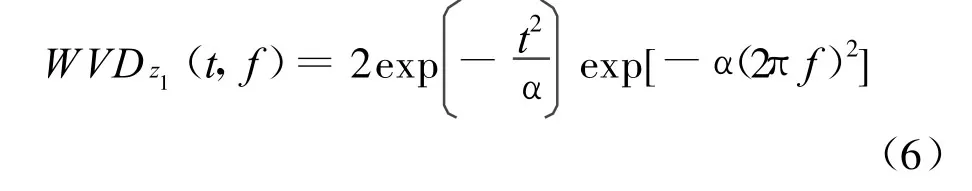
2t0）的Wigner-Ville分布为:

为了方便分析,选取受单一频率调制的高斯信号作为第1个信号,其时宽为a=15 s,时延为t1=40 s。第2个信号与第1个信号相同,时延为t2=70 s,与第1个信号在时间上相隔30 s。这2个信号之和的Wigner-Ville分布,如图1所示。2个信号产生交叉项与2个自Wigner-Ville分布项处于相连与非相连的临界状态,只有当2个信号时间相隔大于30 s时,才能将2个信号区分开来,从而交叉项影响了分辨率。

对于短时傅里叶变换,选择高斯函数作为窗函数,即

图1 交叉项对Wigner-Ville分布分辨率的影响

则单个高斯信号的短时傅里叶变换为:

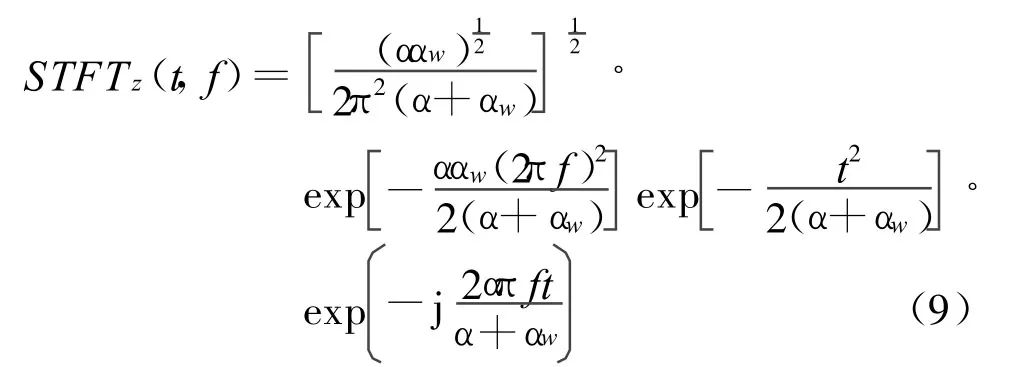
相应的单个高斯信号的谱图为:

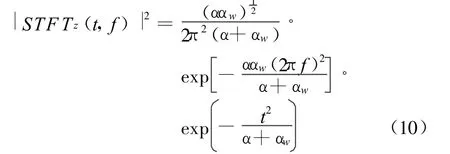
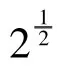
它们与信号和窗函数的时宽有关。在信号一定的情况下,窗函数时宽越窄,谱图的时间分辨率越高,频率分辨率越低。对于多个信号的情况,短时傅里叶变换不产生交叉项,谱图的交叉项仅出现在信号自谱图项重叠的区域,对谱图的时间分辨率和频率分辨率没有影响。

以时宽αw=25 s的高斯函数作为窗函数,2个信号与图1中所用的2个信号完全相同。2个信号之和的谱图如图2所示。这2个信号没有重叠区域,也就没有交叉项。即便2个信号有重叠区域,交叉项也仅限于重叠区域。因此,信号的多与少对分辨率无影响。

图2 谱图分辨率示意图

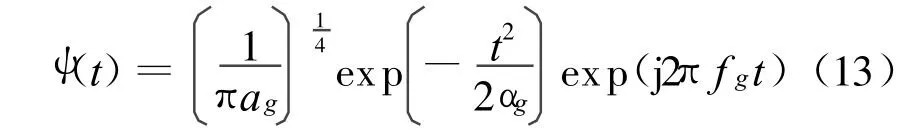
为了考察小波变换的在时频平面上的特性,采用改进小波变换。单个高斯信号的改进小波变换为:

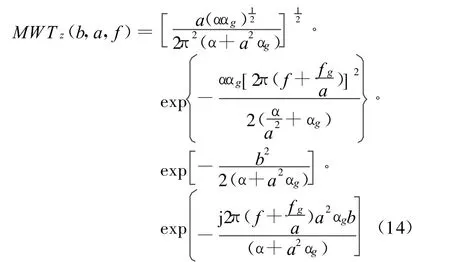
对于小波变换,选择调制高斯函数作为基本小波,即:

相应的单个高斯信号的改进尺度图为:

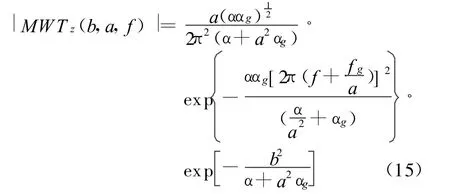
它们与信号的时宽、基本小波的时宽及尺度参数有关。在信号一定的情况下,基本小波时宽越窄,尺度图的时间分辨率越高,频率分辨率越低。当尺度参数较大时,位于尺度图的低频端,尺度图频率分辨率高,时间分辨率低；当尺度参数较小时,位于尺度图的高频端,尺度图频率分辨率低,时间分辨率高。对于多个信号的情况,小波变换不产生交叉项,尺度图的交叉项仅出现在信号自尺度图项重叠的区域,对尺度图的时间分辨率和频率分辨率没有影响。

为了反映尺度图的时间分辨率和频率分辨率变化情况,取 4个调制高斯信号z1（t）、z2（t）、z3（t）、z4（t）,它们的时宽均为α=15 s。z1（t）与z2（t）有相同的调制频率,z3（t）与z4（t）有相同的调制频率。z1（t）与z3（t）有相同的时延,t1=t3=40 s。z2（t）与z4（t）有相同的时延,t2=t4=76 s。以调制高斯函数作为基本小波,时宽为 αg=11 s。这4个信号之和的尺度图如图3所示。图3所示结果反映了尺度图时间分辨率和频率分辨率变化的规律,交叉项不会出现在自尺度图项非重叠区域。

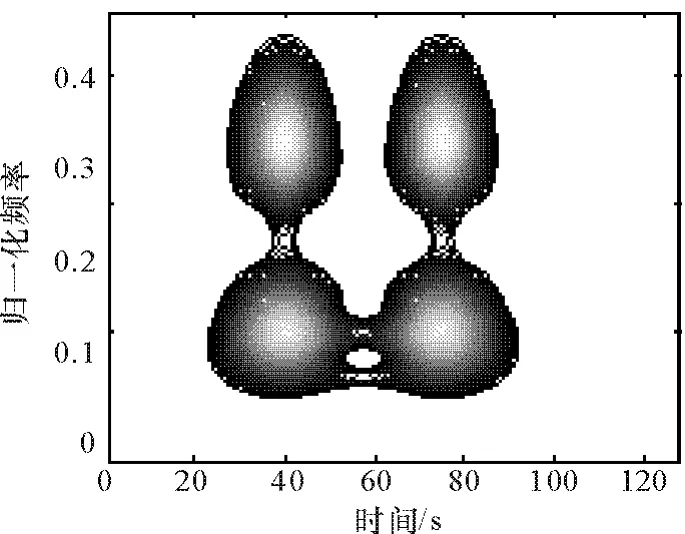
图3 尺度图分辨率示意图

3 结 论

本文利用时频聚集性较好的高斯函数作为标准信号,统一分析、比较了短时傅里叶变换、小波变换、谱图、尺度图、Wigner-Ville分布的分辨率,尤其是通过改进小波变换使时间-尺度分布与时频分布分辨率可以统一比较,给出了时间分辨率和频率分辨率的表达式。时频分布分辨率的比较,为在信号分析与处理中选择合适的分析方法提供了依据。

[1] Hlawatsch F,Boudreaux Bartels G F.Linear and qaudratic time-frequency signal representations[J].IEEE Signal Processing M agazine,1992,9（4）:21-67.

[2] Cohen L.Time-frequencydistributions—— areview[J].Proceedings of the IEEE,1989,77（7）:941-981.

[3] Shie Qian,Dapang Chenl.Joint time-frequency analysis[J].IEEE Signal ProcessingMagazine,1999（3）:52-67.

[4] Mallat S.A Wavelet Tour of Signal Processing[M].Burlington:Academic Press,1999.

[5] 张贤达,保铮.非平稳信号分析与处理[M].北京:国防工业出版社,1998.

[6] Cohen L.Time-FrequencyAnalysis[M].New Jersey:Prentice-Hall,1995.

[7] Jones D L,Parks T W.A resolution comparison of several time-frequency representations[J].IEEE Transactions on Signal Processing,1992,40（2）:413-420.

[8] Mallat S.A theory for multiresolution signal decomposition:the wavelet representation[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1989,11（7）:674-693.

[9] Daubechies I.The wavelet transform,time-frequency localization and signal analysis[J].IEEE Transactions on Information Theory,1990,36（2）:961-1005.

[10]Kadambe S,Boudreaux-Bartels G F.A comparison of the existence of"cross terms"in the Wigner distribution and the squared magnitude of the wavelet transform and the short time Fourier transform[J].IEEE Transactions on Signal Processing,1992,40（10）:2498-2516.