山西不同地区太阳辐射量及最佳倾角分析
2011-04-25刘振宇冯华杨仁刚
刘振宇,冯华,杨仁刚
(1.山西农业大学 工学院,山西太谷 030801;2.中国农业大学 信息与电气工程学院,北京 100083)
在能源危机和环境污染日益严重的双重压力下,能源问题已成为制约各国家和地区经济发展的关键因素。开发利用太阳能能源,是解决上述问题的有效途径之一。山西省蕴藏着丰富的煤炭资源,但是化石能源毕竟是有限的,同时它的使用严重破坏了该地区的生存环境[1]。太阳辐射资料是太阳能利用中的重要科学依据之一,获得太阳辐射数据的方法主要有实地测量和理论模拟计算两种。国内外许多研究人员采用理论方法、理论和统计方法相结合的方法、神经网络、人工智能等优化算法建立模型[2]。相关模型多数属于半理论半经验公式,并且受地域和气候类型的影响,不同地区计算值和实测值误差较大。本文针对山西不同地区水平面上太阳辐射量和最佳倾角进行了计算分析和软件开发,为山西的太阳能工程计算提供预测数据,并为相近地区太阳辐射计算提供参考[3]。
1 太阳辐射量模型和最佳倾角模型
1.1 太阳辐射量气象学模型
太阳辐射是以平行光的方式到达地球表面的,太阳平行光与水平面的交角称为太阳高度角,常称为太阳高度。太阳高度角与该地的地理纬度(ψ)、赤纬(δ)以及当时的时刻(以时角 ω表示)有关,太阳高度的计算公式为:

式中:太阳高度角变化在0°至90°之间,太阳在地平线以下,在一定范围内也可用负值表示。太阳高度角的大小影响到达地面能量的多少,太阳高度角越大,地面单位面积上获得的太阳辐射量就越多。
δ为求算日期的赤纬,它是太阳光线垂直照射地球的位置,用阳光直线点的地理纬度表示。赤纬在北半球取正值,在南半球取负值。在一年里太阳赤纬在+23.5°~ -23.5°之间变动。春分日和秋分日,太阳直射赤道,δ=0°;夏至日,太阳直射北回归线,δ=+23.5°;冬至日,太阳直射南回归线,δ=-23.5°。赤纬角计算公式为:

式中N°以度为单位,是指距春分日或秋分日最近的总天数。春分日至秋分日取正值,否则,取负值。
ω为所求时间的时角,即把时间换算为角度:按地球24 h转过一周 360°,每小时为 15°,以当地真太阳时正午为 0°,下午为正,上午为负。即:正午 ω=0;上午:ω<0;下午 :ω>0 。

式中的当地太阳时采用24小时制。
正午时刻h的计算公式为:
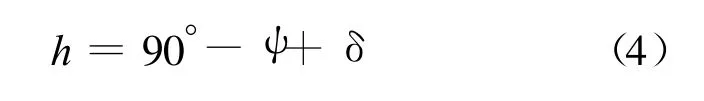
日出、日落时刻,太阳正好位于地平圈上,水平面上太阳高度角为0,即
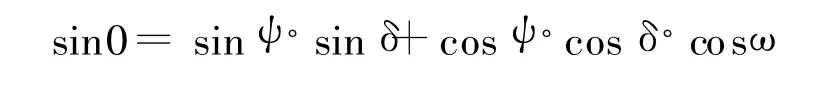
求解上式得:

上式计算后得到+ωs和 -ωs两个值,+ωs为日落时角,-ωs为日出时角。
影响太阳辐射在大气中减弱的因素主要是大气光学质量(简称大气质量,m)和大气透明程度(简称大气透明系数)。大气质量m为:
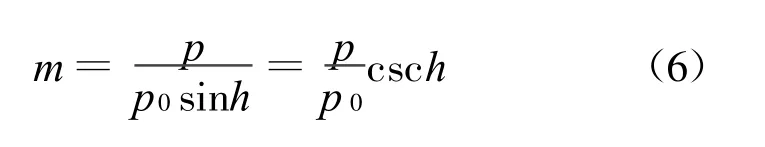
其中,p为观测点的大气压,p0为标准大气压。
大气透明系数(P)表明太阳辐射通过大气后的削弱程度,是以阳光透过一个大气质量后的辐射度与透过前的辐射度之比表示的,为小于1的数,即:

式中:Pm是第m个大气质量的透明系数;Sm,Sm-1分别表示阳光透过第m个大气质量后和之前的辐射度。大气上界太阳辐射通过m个大气质量的太阳辐射量为:

式中S0为大气上界的太阳辐射照度(其值近似的等于太阳常数,通常采用1367 W◦m-2)。又因太阳辐射通过大气层被减弱后,约有45%左右可到达地面,则可通过(8)式近似得出大气透明系数P值。
到达地面的太阳辐射有两部分组成即太阳直接辐射和天空散射辐射,两者之和称为太阳总辐射。到达水平面上的太阳直接辐射辐照强度可用式(9)求得:

大气对太阳散射的一半可以到达地面,由此可以得到散射辐射的近似式:

同时到达地面的太阳总辐射强度是太阳直接辐射强度和天空辐射强度的总和[4]。

1.2 最佳倾角模型
朝向赤道倾斜面上的太阳辐射量,通常采用Klein[5]的计算方法,倾斜面上所接受到的太阳辐射总量HT由直接辐射量Hbt、天空散射辐射量Hdt及地面反射辐射量Hτt组成,即:

Hbt与水平面上的直接辐射量Hb(Hb=S′)之间有如下关系:

对于朝向赤道的倾斜面,Rb可以由下式确定:

式中,ψ是当地纬度,β是倾角,δ是太阳赤纬。
水平面上的日落时角:

倾斜面上的日落时角:

Hay模型认为倾斜面上天空散射辐射量是由太阳光盘的辐射量和其余天空穹顶均匀分布的散射辐射量两部分组成,可表达为
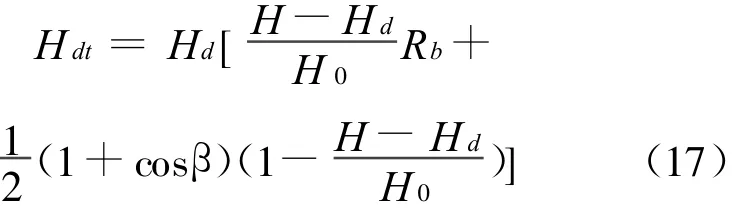
式中Hb和Hd分别为水平面上直接和散射辐射量;Rb为倾斜面与水平面上直接辐射量之比,H0为大气层外水平面上太阳辐射量;β为倾角。
大气层外的水平辐射量可由下式求出:

其中,S0为太阳常数。
地面反射辐射常量的表达式为:

式中,ρ为地面反射率,一般情况下ρ=0.2[6]。
倾斜面上太阳辐射总量的表达式为:

由上式直接求出对应的最大太阳辐射倾角的数学表达式有些困难,在冬半年,太阳赤纬为负值。如当地纬度为 ψ,通常总有 ω(ψ-β)<ψ,因此倾斜面上日落时角ωs和水平面日落时角ωst相等,这是可直接推导出最佳倾角的数学表达式。
将式(19)改写为:

式中HT为水平面上的总辐射量。
对于确定的地点,其太阳辐射量及地面反射率等均为常数,将HT对β求导,并令=0,得:

当直接辐射量为0时,最佳倾角不等于0,这正是天空散射辐射量各向异性模型所需的结果。对于夏半年,最佳倾角往往接近于0,甚至为负值,由式(22)直接计算最佳倾角也有其实用价值[7]。
2 山西地区太阳辐射量经验公式及软件开发研究
通过Matlab编程,结合气象学模型得到山西省不同地区一年的日小时平均太阳辐射量理论值,并与山西省各地区2009年全年的实测值分别拟合回归。由于山西各地区纬度和海拔等的差异,以太原地区为对象对太原太阳辐射量经验公式进行讨论。其它地区计算方法相同。经分析计算得到太原地区太阳辐射量理论数据的拟合公式和修正系数[8]。
理论拟合公式为:

修正系数为:

则可得经验公式为:

经验公式校验:选择一组是由经验公式得到的数据,另一组是太原地区一年太阳辐射量的实测值。采用成对数据t检验,先作出两组数据之差,然后检验假设h1∶μ=0;h1∶μ≠0。给定水平为α=0.05。校验公式为:
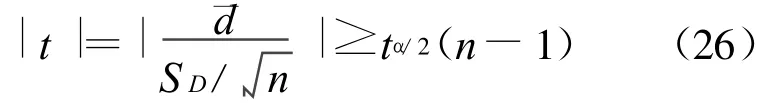
式中¯d和SD分别为样本均值和样本方差。
经Matlab编程计算得 h=0,置信区间为(-75.5783,68.5553),故接受h1。认为两组数据无显著差异,认为建立的太阳辐射计算公式的效果是显著的。该公式能作为太原地区太阳辐射量经验公式使用[9]。
为简化计算,山西各地区太阳辐射量的计算、经验公式的获得及最佳倾角计算,均采用Matlab编程软件实现。编程计算流程如图1所示。
3 山西地区太阳辐射量和最佳倾角

图1 山西各地区太阳辐射量经验公式及最佳倾角程序流程图Fig.1 The program flow chart of the solar radiation empirical formula in Shanxi area and optimum tilted angle
根据太阳辐射量气象学模型和相关最佳倾角计算模型,对山西省不同地区的最佳倾角和水平面太阳辐射总量作了分析和计算。表1和表2列出了山西各市的最佳倾角和各月水平面平均日辐射量[10]。
根据山西各地区的太阳能辐射情况,在一年中分别选取全晴天的典型日期(表3)作为每个月的代表日[11],可以计算出山西不同地区全年各月的最佳倾角,优化后的月最佳倾角既可以应用于固定式太阳能光伏发电系统,也可应用于极轴跟踪方式中每个月的调整。只要在太阳能光伏板上安装简易的调节装置就可实现一年各月倾角的调整。

表1 山西各地区的最佳倾角Table 1 Yearly optimum tilt angle in each city of Shanxi province
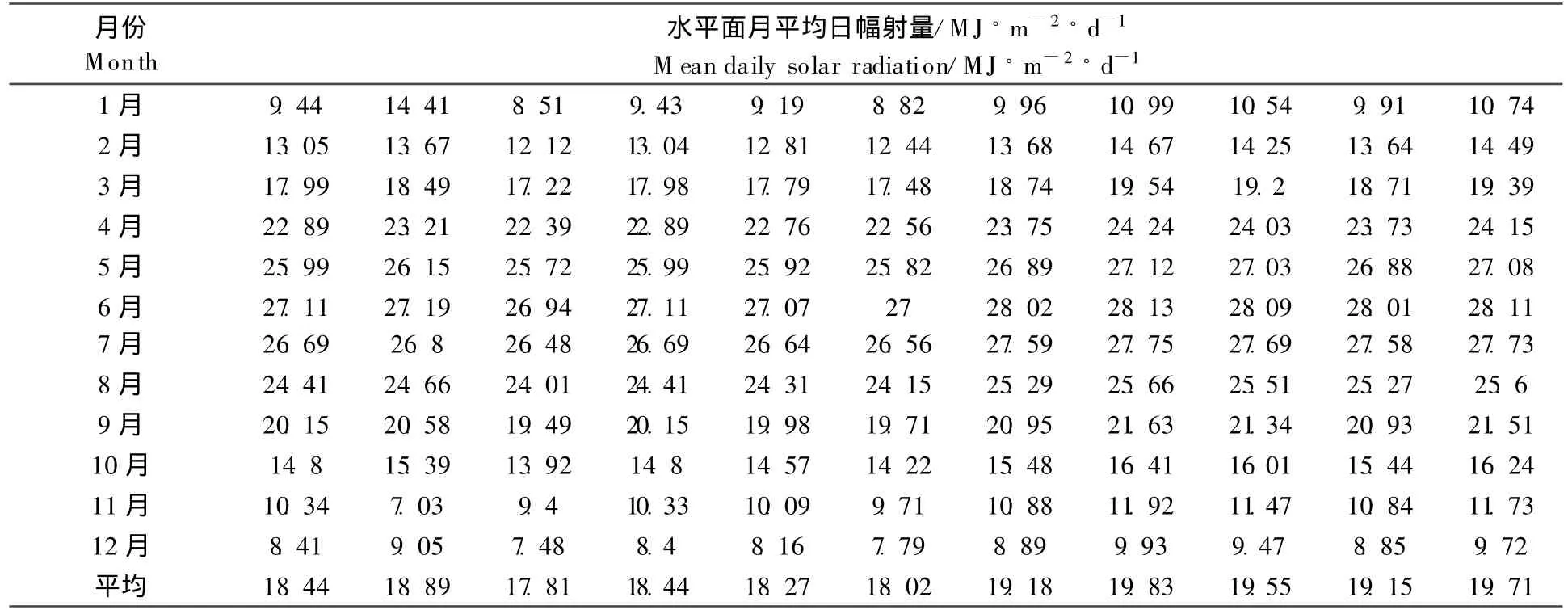
表2 山西各地区水平面月平均日辐射量Table 2 Mean daily solar radiation on a horizontal surface in each city of Shanxi province

表3 月代表日的日序Table 3 Sequence number of representative day in every month and a year
4 结论
(1)根据太阳辐射量气象学模型,探讨了山西省各地区太阳辐射量的计算方法,并建立了相应的计算模型。对山西各地区太阳辐射量进行了理论计算,并且与各地区某一年太阳辐射量的实测值分别进行了拟合回归,进行了理论公式的修正,得到了修正系数,进而得到了山西各地区对应的太阳辐射量计算经验公式。经过检验,经验公式的计算效果是显著的,精度较高,相关性达95%以上。
(2)根据Klein的朝向赤道倾斜面上太阳辐射量的计算方法和Hay天空散射各向异性模型的计算方法,采用求导的方法对山西省不同地区的太阳能光伏板的最佳倾角进行了分析计算,结果与其他研究者计算结果[7,12,13]接近,并可得出大多数地区最佳倾角小于当地纬度。虽然本文采用的求导法计算量较少,但不够精确,仍需要继续改进。
(3)对太阳辐射量与最佳倾角计算进行了软件开发研究。软件开发中计算模型结合了山西各地区气象资料,具有山西地域特征,减小了其它模型由于适用范围所引起的较大误差。经验公式的获得与最佳倾角的获得为我省在太阳能资源的开发与利用方面提供了一定的参考价值。综合气象台太阳能资源参数计算结果、气候调研和本文数值模拟等方面的分析成果,山西省太阳能资源总储量北、中部偏少,南部偏多,太阳能资源技术可开发量巨大。
[1]杨卫国,夏红卫,魏生贤,等.竖直墙面不同方位上太阳辐射量的计算分析[J].西南师范大学学报:自然科学版,2008,33(2):22-25.
[2]贾友见,聂林如,黄仕华.计算水平地面散射辐射量的模型[J].昆明理工大学学报,2000(5):40-42.
[3]后尚,田瑞,闫素英.呼和浩特地区太阳辐射量模型分析[J].可再生能源,2008,26(2):79-82.
[4]刘江,许秀娟.气象学(北方本)[M].北京:中国农业出版社,2002:13-37.
[5]Klein S A.Calculaton of monthly average insolationon tilted surfaces[J].Solar Energy,1977,19(4):325-329.
[6]杨金焕.固定式光伏方阵最佳倾角的分析[J].太阳能学报,1992,13(1):86-92.
[7]杨金焕,毛家俊,陈中华.不同方位倾斜面上太阳辐射量及最佳倾角的计算[J].上海交通大学学报,2002,36(7):1032-1036.
[8]太阳能利用协作小组.我国各地大气透明系数资料[J].气象科技,1980(6):32-33.
[9]郭力民,陈胜军,顾骏强,等.浙江太阳辐射量计算方法的探讨[J].科技通报,1991,7(2):90-96.
[10]孙韵琳,杜晓荣,王小杨,等.固定式并网光伏阵列的辐射量计算与倾角优化[J].太阳能学报,2009,30(12):1597-1601.
[11]周芳,胡明辅,周国平.铅垂面上太阳辐射量计算方法探讨[J].建筑节能,2007,35(5):55-59.
[12]申政,吕建,杨洪兴.太阳辐射接受面最佳倾角的计算与分析[J].天津城市建设学院学报,2009,15(1):61-64.
[13]汪东翔,董俊.固定式光伏方阵最佳倾角的选择[J].新能源,1994,16(4):4-6.
