电力系统谐波状态估计量测配置算法研究

汪 瑶 侯世英 黄丹梅

（1.中国煤炭科工集团重庆设计研究院，重庆 400016；

2. 重庆大学电气工程学院高电压与电工新技术教育部重点实验室，重庆 400044）

1 引言

随着电力系统谐波污染问题日益严重，为及时解决电网谐波治理难题，准确分清谐波责任，首先得明确电力系统中谐波的分布状态。而在大多数情况下谐波源是未知的，对于这样的问题，采用谐波状态估计则是一种有效的分析手段[1-2]。自从G．T．Heydt首次提出电力系统谐波状态估计概念用于谐波源识别以来 ，谐波状态估计引起了许多学者和电力工作者的兴趣[1-6]。电力谐波状态估计技术就是根据有限的谐波测量数据来估计整个电网谐波分布，达到对整个系统进行谐波监测和谐波管理的目的。早期的谐波状态估计技术将谐波有功功率和无功功率作为测量量，但谐波无功功率的定义存在争议且其测量装置没有统一的标准，因而采用无功功率的方法没有说服力。随着基于全球定位系统的同步相量测量单元PMU（Phasor Measurement Unit）技术的发展，使得全系统范围内的相量测量成为了可能，目前的谐波状态估计都避开了将功率作为测量量，而是对母线谐波电压、支路谐波电流和注入谐波电流进行同步相量测量，使得估计方程成为线性方程，采用最小二乘法[7]、奇异值分解SVD(Singular Value Decomposition)[8-9]等算法求解系统未知状态。在此基础上，着重研究了PMU的优化配置问题，以保正系统可观测的情况下，提高谐波状态估计的精确性与经济性。

2 谐波状态估计可观性分析

可观性分析可定义为在给定的网络拓扑结构和量测配置的前提下，判断利用量测数据确定母线状态的能力和程度。当收集到的量测量通过量测方程能够覆盖所有母线的电压幅值和相角时，则通过状态估计可以得到这些值，称为网络是可观的[10]，否则称为不可观。网络的可观取决于网络结构及量测配置。

谐波状态估计可观性分析技术主要可分为数值方法和拓扑方法两类。数值可观性分析算法比较繁琐，需要较大的计算量；拓扑可观性分析算法，计算过程较为简易。

3 相量量测装置配置算法

3.1 量测配置问题的评价指标

PMU利用GPS系统提供的高精度授时信号，实现了对电力系统各个节点数据的同步采集，如果在每个节点都安装 PMU，则系统就是完全可观测的，不需进行任何计算。但由于经济的原因，目前乃至相当长的一段时间内，不可能在系统的所有节点均装设PMU。因此， PMU测点的最小配置和最优配置问题受到了国内外学者的广泛关注[11]。

量测装置的最优配置通常和可观性分析紧密联系在一起的。量测装置最优配置研究如何在电力系统中选择量测装置的安装地点，使用最少数目的量测装置确保各量测装置系统可以提供足够的量测，使得被研究的电力系统可观测。

评价量测系统是否最优，可从以下几个方面考虑：①状态量的估计精度；②可靠性与数值稳定性；③经济性。

量测点的优化配置是一个复杂的问题，通常在良好状态估计的性能和昂贵的整个系统的造价之间难于取舍。以下就主要研究在保证系统可观测的条件下，从经济性以及量测方程的数值稳定性的角度实现系统最优的量测配置。

3.2 量测装置的优化配置算法

为了得到系统最优的配置方案，可采用穷尽搜索的方法，这种方法通过确定目标函数（估计的精度、成本问题、量测方程的数值稳定性等方面）从而试尽所有可能的组合，最后确定在给定量测配置数目下的一个最优解。而这对于有N条母线的系统，M个可放置量测装置的位置以及P个给定的量测装置数的情况下，就必须要计算种组合才能确定最佳的配置位置，这种方法的搜索过程是很耗时的。文献[12]提出一种序贯搜索的方法，该算法的基本思想是在最优的（M+1）个量测位置中，一定包含了最优的M个量测位置，而且当系统增加或者减少量测时，该方法不用重复的从新开始搜索，而它提供的解通常都是最优或接近最优的。序贯方法与穷尽搜索法相比，以同样的而系统而言，序贯方法只需要计算P( 2M+ 1−P)/2种配置的组合便可得到系统的最优配置点，可大大提高搜索的效率。

同时，鉴于谐波状态估计量测方程的数值稳定性（量测方程条件数越小，方程数值稳定性越好）以及测量的经济性，在考虑量测配置方案的时候，应该首先考虑可提供量测点数量最多的子站，即主要子站，其次根据状态变量的个数来确定量测配置点的数量，使得保证系统完全可观测情况下的量测配置的成本尽可能低。因此，本文以量测方程数字稳定性为指标，结合最小量测子站和序贯搜索方法的思想，提出以下的优化配置算法程序：

（1）选择能提供最多量测点的子站的全量测作为算法的初始搜索域。

（2）可观性算法判断所选子站的全量测能否使系统状态量完全可观测，如可观，则转向步骤（3）；如不可观，则追加一个可提供次多量测点的子站，重复步骤（2）。

（3）读入网络结构、网络参数和需配置的量测点的数目等信息与数据，得到系统的全量测矩阵。

（4）依次临时地删除量测矩阵的一行（即量测配置点），计算相应矩阵的条件数，如Cond1（量测矩阵的第一行被临时删除），Cond2，…，Condm（量测矩阵的第m行被临时删除）。

（5）在步骤（4）中，若某列的删除使得量测矩阵具有最小条件数，则该列就被永久删除。

（6）重复进行步骤（4）－（5），直到量测配置点的数目等于状态变量的数目。

（7）输出量测点的配置的结果。

程序框图如图1所示。

以上量测配置算法，在每一次循环中，都会排除一个量测点，可放置量测配置的点数由M开始到M-1，M-2，…，M-(M-P)，配合可观测性算法，则最后剩下的P个量测点就能够保证系统在可观测的条件下（量测矩阵的所有奇异值非零[12]），量测矩阵的条件数达到最小，从而实现系统量测的最优或近优配置。

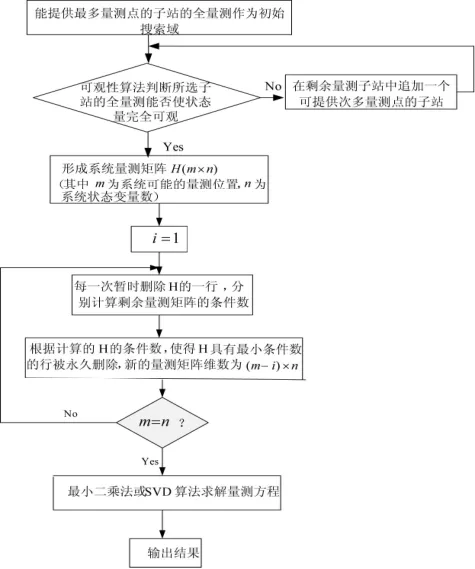
图1 量测配置程序框图

4 算例分析

4.1 仿真系统

本文选用IEEE 14节点系统[13]用MATLAB7.0进行仿真验证。此系统为三相完全对称系统，包含有两个谐波源，一个为接在母线3的12脉波的HVDC（高压直流）终端，另一个为接在母线8的SVC（静止无功补偿器）。

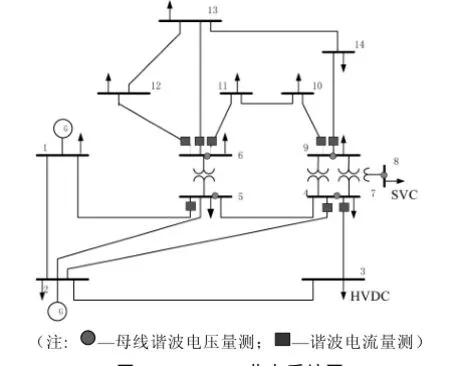
图2 IEEE 14节点系统图

4.2 系统元件模型

传输线用π型等效模型代替；发电机用松弛母线或PV总线的模型等效；变压器使用短路阻抗模型等效，通过具体绕组的连接考虑了变压器对谐波电流相位的影响，变压器的饱和特性也可以得到模拟；负荷模型通过常数值的有功、无功功率以及额定电压来体现，其谐波阻抗的值如文献[14]所示确定；谐波源HVDC通过两个6脉波整流桥来等效代替[15]，谐波源SVC包含有滤波器和Δ连接的TCR,具体的谐波分析中，可以用一个常数值的无功负荷和一个谐波电流源代替。

通过Matlab7.0中的Sim Power Systems 模块搭建的仿真系统来模拟实际系统的运行情况，通过仿真得到的系统节点注入谐波电流幅值如图3所示。

图3 节点注入谐波电流幅值仿真值

4.3 程序仿真结果

考虑到谐波电压随谐波次数的增加在电网中的衰减速度大大超过谐波电流的衰减速度[16]，而且有关测试试验也表明，由于高次谐波电压衰减快，离谐波源10～50km的可靠量测距离对13次以上的谐波已经不再适用，所以，选择节点注入谐波电流作为估计量（状态变量），以能够更好的判断电网中的谐波状态[16]。由图 2可知，系统有 14条母线，其中母线7为变压器内部母线，为非谐波源母线，为降低方程的维数，选取状态变量数（母线谐波注入电流）为13个，则为了保证系统的完全可观测，至少需要13个量测点，同时为了最小化系统的量测子站的数量，首先从网络的结构特点考虑，如表(3.1)，子站（母线4，7-9）共同使用一个量测子站，该子站共提供了22个可供量测的位置，应首先纳入考虑之中。如果在子站（母线4，7-9）每个量测点都放置量测装置，计算量测方程的条件数（以5次谐波为例）为 4.28× 1018，量测矩阵是奇异的，用可观性算法判断在该子站的全量测不能保证系统状态量的完全可观测，应考虑多加入一个量测子站（母线5-6），该子站可提供12个量测点，采用可观性分析算法，对母线 4-9的全量测能够保证系统的完全可观测，即量测矩阵的所有奇异值非零，计算量测矩阵的条件数为93.25，因此可把子站（母线4-9）的全量测作为优化配置程序的初始搜索域，采用提出的量测配置优化算法，得到系统最优量测配置点为：母线电压量测4-6，8-9，支路电流量测4-2，4-3，5-1，6-11，6-12，6-13，9-10，9-14。

根据以上的配置程序，得到系统可观测时的母线注入谐波电流幅值估计值如图4所示，其估计误差如图5所示。

图4 优化配置时节点注入谐波电流幅值估计值

图5 优化配置时节点注入谐波电流幅值估计误差

此外，全量测的基础上，如随机选取13个测量点，进行谐波状态估计，其节点注入谐波电流估计值误差如图6所示。

图6 随机选取量测点时节点注入谐波电流幅值估计误差

5 结论

由图4可知，在保证系统可观的情况下，应用提出的优化配置算法，不仅能够大大节省量测配置的搜索步骤，同时能保证系统状态量的估计精度，正确的识别谐波源。与之相比较，在随机选取测量点，其量测方程奇异的情况下（图 5），虽也能准确识别谐波源，但其估计的误差却大大增加了。

本文是采用IEEE14节点的系统仿真，只有14个状态变量，如果实际的系统有几十甚至几百个节点，则如要保证系统的完全可观测，就需要几十或几百的量测点（或量测通信通道），这种投资成本是相当巨大的。因此，还有必要研究系统在量测不足情况下的谐波状态估计算法，以保证估计精度情况下的成本最小化。

[1] Z. P. Du, J. Arrillaga, and N. Watson, Continuous harmonic state estimation of power systems [J].IEE Proceedings–Generation Transmission and Distribution, 1996.7, 143(4) :329-336.

[2] 祝石厚,侯世英,吕厚余. 电力系统谐波分析的有效方法-谐波状态估计技术综述[J].现代电力,2007, 24(3): 6-10.

[3] Kent K C Yu, Watson N R, Arrillaga J. An adaptive Kalman filter for dynamic harmonic state estimation and harmonic injection tracking[J]. IEEE Trans on power Delivery,2005,20(2):1577-1584.

[4] 侯世英,汪瑶,祝石厚的，等基于相量量测的电力系统谐波状态估计算法的研究[J].电工电能新技术，2008,27(2):42-46.

[5] Ma Haili,Girgis A A.Identification and tracking of harmonic source in a power system using Kalman fiiter[J].IEEE Trans on power Delivery,1996,11(3): 1659-1665.

[6] 周念成,谭桂华,赵渊等. 一种计及参数误差的电网谐波状态估计方法[J].重庆大学学报, 2009,32(2): 146-150.

[7] 吴笃贵, 徐政.基于相量量测的电力系统谐波状态估计(I)-理论、模型与求解算法[J].电工技术学报, 2004, 19(2):64-68.

[8] 徐志向,侯世英,周林等. 基于奇异值分解的电力系统谐波状态估计[J]. 电力系统自动化设备, 2006,26(11): 28-31.

[9] 徐志向. 基于奇异值分解算法的谐波状态估计及谐波源定位的研究[D]. 重庆：重庆大学，2006.

[10] 吴笃贵,徐政. 基于相量量测的电力系统谐波状态估计(II)-可观性、质量评估与算例研究[J]. 电工技术学报,2004,19(3):76-81.

[11] Ki-Seon Cho, Joong-Rin Shin, Seung Ho Hyun. Optimal placement of phasor measurement units with GPS receiver[C], Power Engineering Society Winter Meeting, 2001,1: 258-262.

[12] C. Matharad ,S. Premrudeepreechacharn, N.R. Watson, power system state estimation using singular value decomposition[J], Elect. Power Syst. Res.,2003, 67(2):99-107.

[13] R. Abu-hashim, R. Burch, G. Chang, Test Systems for Harmonics Modelling and Simulation[J], IEEE Transactions on Power Delivery, 1999.4, 14( 2): 579-581.

[14] CIGRE Working Group 36-05,Harmonics Characteristic Parameters, Methods of Study Estimates of Existing Values in the Network, Electra [J], 1981.7, 77: 35-54.

[15] W.Xu, J.E.Drakos, Y.Mansour, A Three-Phase Converter Model for Harmonic Analysis of HVDC Systems[J], IEEE Trans. on Power Delivery, 1994.7, 9(3):1724-1731.

[16] G.T.Heydt. Identification of Harmonic Sources by a State Estimation Technique [J], IEEE Trans on power delivery, 1989.1,4(1): 569-576.