基于复杂网络理论的军事力量部署研究*

邢焕革，邱 原

（海军工程大学，湖北 武汉 430033）

军事力量部署是形成有利的军事态势，赢得战场主动权，支配战场形势，实现军事目的的前提条件和中心任务，对作战全局具有重要意义。战争实践表明，军事力量部署直接影响军队的作战能力。军事力量部署就是对军事力量在空间或时间上进行最有利的组合，在合适的时机和合理的空间位置上，使之相互配合、支援、策应，同时又可牵制、分散、动摇敌军。实际上，军事力量部署在空间位置上的相互配合、支援、策应，就是复杂网络的一种基本形态。本文运用复杂网络理论，将军事力量部署进行网络拓扑化，通过分析计算网络关键节点的组成来研究军事力量在空间部署的合理性，以定量的方式从整体上研究军事力量部署，进行有益的研究和探索。

1 军事力量部署网络结构描述

运用复杂网络理论对军事力量部署进行网络特征描述，关键在于如何体现各军事力量单元在空间部署上的相互配合、支援和策应的关系。依据网络理论，将分布在不同地域的军事力量单元作为网络节点，将军事力量单元连接为整体的公路或铁路称为网络的边。因此，将军事力量部署在空间上相互配合、支援、策应的关系可以通过网络拓扑结构进行描述。为研究问题的方便性，本文只讨论陆上军事力量部署情况。

定义由节点集V=( v1,v2,···,vn)和边集E=( e1, e2,··,en)组成网络 G =( V,E)。其中，节点 vi表示部署在不同地域上的军事力量单元； eij表示军事力量单元(vi, vj)在空间位置上相互配合、支援和策应的关系。如果它们之间有公路或铁路连接，则这两个节点之间有边相连，否则无边（这里假设任意两个节点之间只有一条边相连）。因此，对军事力量部署网络的基本特征有如下认识：

1）若网络中任意两个节点之间只有一条边存在，可以认为此网络为无环的连通网络；

2）分布在不同地域之间的军事力量单元可以通过公路或铁路形成相互配合、支援、策应关系，由此确定网络的边是双向的，可以等效为无向网络；

3）虽然部署在不同地域上的军事力量单元之间的距离不同，但为了研究军事力量部署空间上的合理性，本文不研究军事力量部署时机的影响，因此可以认为此网络的边是无权重的。

2 军事力量部署网络关键节点数学模型及计算流程

2.1 网络结构关键节点的概念

不同地域之间的军事力量单元在空间上相互配合、支援和策应的关系表现为网络节点之间的相互关联性，特别是部署的主力更是网络中的关键节点，而相互配合、支援和策应的军事力量单元之间的这种关系表现为相互连通的节点之间存在着重要的依存关系。这种重要的依赖关系主要存在于相邻（也就是直接相连的节点）节点之间。因此，在网络结构中如何寻找关键节点是本文研究的重点。

关于度量网络节点重要程度的特征参量有不少[1-3]，如节点的度、平均路径、聚集系数、介数等，但都存在不能从全局、整体上衡量节点重要程度的问题[4-6]。为此，本文运用节点度的概念和节点介数的概念定义网络的关键节点，并构建计算关键节点的数学模型。

由节点集V=(v1,v2,···,vn)和边集E=(e1,e2,···,en) 所组成的网络G=(V,E)。节点vi的度指的是与相邻节点连接的数目，即该节点连接的边数。

节点vi和vj之间的距离dij定义为这两个节点之间最短路径的边数。如果vi和vj之间不存在连接，则节点vi和vj之间的距离dij→∞。

节点vi的介数表示为：假设节点对vj和vk之间的最短路径有Ljk条。其中有Ljk(i)条经过节点vi，经过节点vi的最短路径数Ljk(i)在节点对vj和vk之间的所有最短路径数Ljk中所占的比例为Ljk(i)Ljk，节点vi的介数Bi是指把经过节点vi对所有节点所占比例累加起来再除以节点对的总数，可以用式（1）表示。

式中n表示的是网络节点的总数。

节点vi的度表征了节点之间具有一定的依存关系，而孤立的节点彼此之间不存在这种重要性的依赖关系。节点之间一旦建立起连接，某个节点的存在与否可能对另一个或多个节点的重要性产生重大影响。星形网络的中心节点就是最明显的例子。如图1所示，如果将星形网络的中心节点去掉，则剩下的节点之间就失去联系，成为孤立的节点，其重要性明显降低。

图1 星形网络结构

因此，一个节点的度在一定程度上表示了该节点的影响力和重要程度，度越大的节点，其影响力也就越大，在网络中的作用也越大，对其相邻节点的影响也越大。同时，一个节点的介数也反映了该节点为网络提供控制能力，而且很多情况下节点对之间的最短路径是唯一的。所以节点介数越大，移除此节点后网络直径变大的可能性就越大，即网络整体性能下降。而节点的介数反映了该节点对网络资源的控制能力，节点的介数越大，表明网络中任意节点对经过该节点的次数越多，对网络资源的控制能力越强，在网络中的起到关键或中心作用，对其相邻节点的影响也越大。可见，节点的介数一定程度上反映了节点的重要程度。因此，网络中的关键节点取决于两个因素：节点的拓扑空间位置和节点的度。节点的度反映了节点的重要程度，介数反映了节点的控制能力。由这两个特征可以决定该节点在整体网络中的地位，即是否为关键节点。

2.2 网络关键节点数学模型

现有的节点重要性评价方法主要是通过比较移除节点前后网络性能的变化情况，而对于节点的移除可能造成的网络被分割的情况需要区别对待，有时难以很直观地表达清楚。将节点的度与节点的介数结合起来确定网络中的关键节点，相当于同时利用了节点的位置信息和度的信息，计算结果可能更加接近真实情况。

网络关键节点数学模型构建的方法：是将节点vi的介数作为该节点的初值，由于该节点有邻居节点存在，因此这些邻居节点通过相连方式对节点vi的介数具有支持作用，其支持作用的大小与邻居节点的介数有关。为此，将邻居节点的介数与度之间的比值作为对节点vi介数支持的大小。因此，网络节点vi的关键节点值Si的数学模型如式（2）所示。

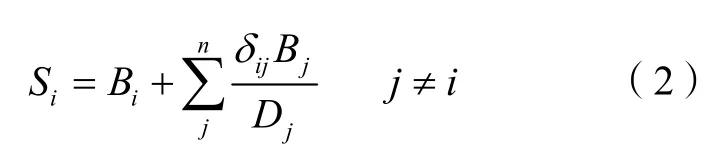
式中，δij表示节点vi和vj是相邻节点的时取值为1，否则取值为0。从式（2）可以看出，一个节点对其相邻节点的影响与此节点本身的介数和度的大小有关。

2.3 网络关键节点计算流程

本文所提出的依据节点介数和相邻节点影响来确定该节点的重要性主要评估流程如下：

1）确定节点vi的度Di；

2）确定网络中所有节点对vj和vk之间的最短路径有Ljk条；

3）确定网络中所节点对vj和vk之间的最短路径经过节点vi有Ljk(i)条；

4）计算节点vi的介数Bi；

5）计算节点vi邻居节点的支持力；

6）计算vi的关键节点度量值Si；

7）比较网络上所有节点关键度量值的大小，确定关键节点。

3 案例分析

下面以1948年辽沈战役前双方军事力量部署情况，针对本文所提出的方法来分析。

如图2所示，解放战争进入到1948年秋，中国大陆的军事形势发生了重大变化。当时东北守敌主要兵力部署如下：由郑洞国率2个军共10万人防守长春，钳制东北野战军主力向南机动；由范汉杰率4个军共15万人防守山海关、绥中、兴城、锦西、锦州、义县等北宁铁路沿线城镇及秦皇岛、葫芦岛两海港，主力防守锦州、锦西地区，维护东北与关内陆上及海上联系；由卫立煌率7个军共30万人防守沈阳及铁岭、抚顺、本溪、辽阳、辽中、新民等外围据点，作为防御中枢，以确保沈阳并支援锦州、长春方面的作战。敌军总的企图是集中兵力，重点守备，以牵制东北我军于关外。

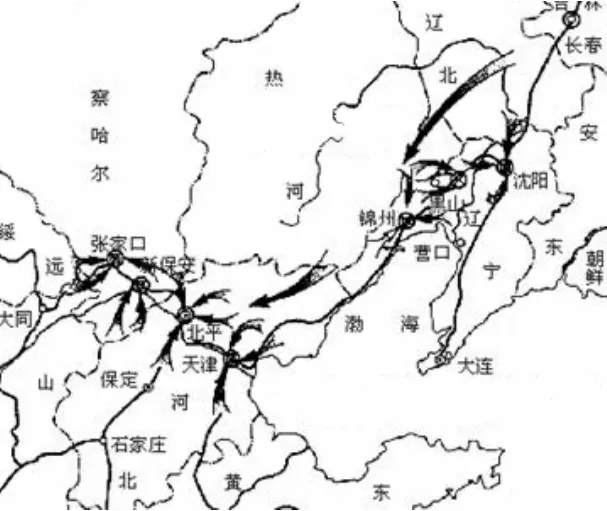
图2 军事力量部署示意

针对敌军的军事力量部署，东北野战军如何选择攻击点是当时决策的重点。运用复杂网络理论将上述军事力量部署进行网络化，如图3所示。

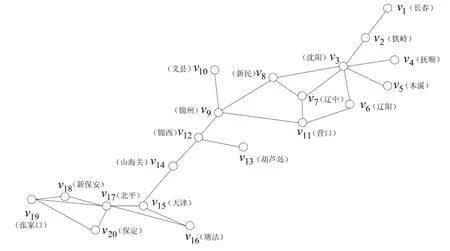
图3 军事力量部署网络拓扑结构图

通过运用本文提出的关键节点计算方法所得到的结果如表1所示。从表1计算结果中可以很清楚发现，网络中的军事力量部署的关键节点分别为v9（锦州）、v12（锦西）、v14（山海关）、v3（沈阳）、v8（新民）、v17（北平）和v15（天津）。通过割裂这些网络中的关键节点之间的联系，可使网络发生崩溃或网络功能显著降低。实际上，从作战的实际情况来看，当时敌方军事力量部署的重点正是在锦州、锦西、山海关，其次是沈阳、新民以及天津、北平等地方。因此，要从战役全局上实现辽沈战役的企图，锦州是重要的战略要点。同时，要攻占锦州，锦西与山海关之间、锦州与锦西之间、沈阳与新民之间的守敌是重要的阻击地点。在实际作战中，在这些地方就有著名的黑山阻击战、塔山阻击战等。运用复杂网络理论分析的结果与当时中央决策是相一致的，表明本文所提出的方法具有一定的应用参考价值。

表1 军事力量部署关键节点计算表

4 结束语

军事力量部署的关键节点表征了部署军事力量单元对整个作战态势的影响程度。本文运用复杂网络理论，定义了军事力量部署网络拓扑化后的关键节点概念，在此基础上提出了基于网络节点度和介数综合数学模型来评价网络节点关键度量值数学模型及基本算法流程。本文所研究的方法仅是一个初步的尝试，还有许多问题需要进一步研究。针对力量部署单元关键节点的力量调整是下一步研究的重要内容。

[1]陈勇,胡爱群,胡啸.通信网中节点重要性的评价方法[J].通信学报，2004，25(8):129-134.

[2]余新,李艳和,郑小平,等.基于网络性能变化梯度的通信网络节点重要程度评价方法[J].清华大学学报(自然科学版),2008,48(4):541-544.

[3]Holme P.Congestion and centrality in traffic flow on complex networks [J].Advances in Complex Systems,2003,(6):163-176.

[4]Newman MEJ.The Structure and Function of Complex Networks [J].SIAM Review (0036-1445),2003,45(2) :167-256.

[5]Albert R,Barabasi A L.Statistical Mechanics of Complex Networks [J].Review of Modern Physics(S0034-6861),2003,74(1):47-97.

[6]汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006.