利用图形分析法计算固体物质的溶解度
2011-04-21严西平
严西平 薛 磊
(江苏省苏州市立达中学江苏苏州215003)
利用图形分析法计算固体物质的溶解度
严西平 薛 磊
(江苏省苏州市立达中学江苏苏州215003)
有关固体物质溶解度的计算,是初中化学中溶液知识部分的重要内容之一,也是教学难点之一,教学效果一直不是十分理想。其主要原因在于,一方面,在现用的教材中关于溶解度的计算问题只字未提,更别说解答的思路和格式的示范;另一方面,对于溶解度的概念及计算相对于溶液的溶质质量分数计算来讲,较为抽象,不太容易理解与掌握。特别是遇到一些数据或过程不太直观的计算题,很多学生都出现了捉襟见肘的尴尬情形。为此我们在教学中尝试了“建模”——即图形分析法,具体如下。
一、图形分析法的理论依据与思考过程
1.理论依据
溶液的特点就是均一性和稳定性。因此,在某一溶液中,任意一部分的溶液的组成及溶质的质量分数都是相同的。对于一定温度下的某饱和溶液中,溶质的质量、溶剂的质量及溶液的质量之比是固定的,存在一定的比例关系。
2.思考过程
图形分析法的思考过程,实际上就是利用数学建模的思想。利用数学的思维方式,将化学的计算题中比较抽象的情景建构成比较形象的数学图像模型,借助于数学的思考与解题方法来处理化学的计算问题。
3.图示思考与分析过程
如果图1表示某温度下的KNO3的饱和溶液,我们可以假设溶液存在一个假想的“膜”,将饱和溶液强行分割为“互不混合”的KNO3和水这两个独立部分,如图2:

图1

图2
如果图1表示某温度下的KNO3的不饱和溶液,我们则可以将其假设分为三部分,即①KNO3固体、②能与固体恰好形成饱和溶液的水、③多余的纯净水,如图3:
在不改变温度的条件下,将KNO3不饱和溶液转化为饱和溶液,可以通过蒸发溶剂或增加KNO3这两种途径。从图形角度考虑,通过移去③,就变成了图4所示的“饱和形状”,或通过添加④填补“空缺”,也能形成如图5所示的“饱和形状”。

图3
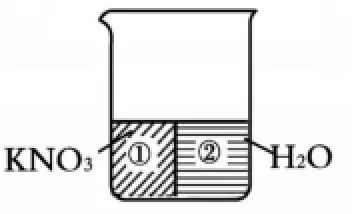
图4
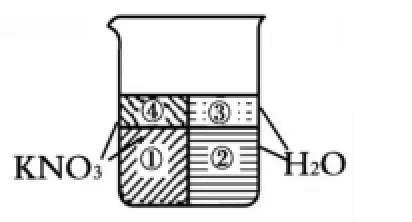
图5
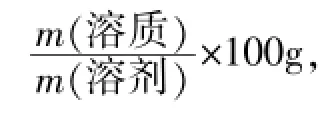
二、例题分析与解答
例1.60℃时,将90gKNO3加入75g水后充分振荡后,仍有7.5g没有溶解,求60℃时KNO3的溶解度。
分析与解答:根据题意,(90g-7.5g)KNO3与75g水混合,恰好能够达到饱和,可画出如图6。根据固体溶解度的定义,只需将图中水的质量“补”为100g,它所对应的KNO3质量便为该温度下KNO3的溶解度,见图7[其中的m4即未溶解的7.5gKNO3,m2+m3=100g,m1+m4=S(KNO3)]。
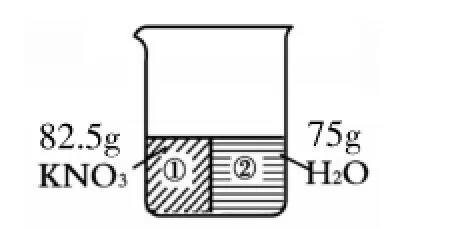
图6

图7
根据如图5的讨论,可得到比例式:

例233℃时,有250g硝酸钾溶液,若向该溶液中加入30g硝酸钾,则恰好达到饱和;若原溶液恒温蒸发掉60g水,也恰好成为饱和溶液。求33℃时硝酸钾的溶解度。


例3NaCl在20℃时的溶解度是36g。在20℃时,将30gNaCl加入到70g水中,充分溶解,所得NaCl溶液中NaCl的质量分数为()
A.26.5%B.30%C.36%D.43%
分析与解答:利用图形分析法,我们可以看出,m1显然小于36g。根据比例,m1/70g=36g/100g,m1=25.2g。故可以用下式直接计算NaCl的质量分数:(当然也可以用25.2g/25.2g+70g计算,结果相同。)


三、结论
通过构建有意义的具象,弥补了初中生抽象思维比较薄弱的不足,对于理解溶液的组成、掌握溶解度的概念和相关计算有积极的促进作用。教学效果较之传统的“公式法”或“列表分析法”有明显的改善,特别是学生容易掌握并能在解题中主动运用图形分析法建构解题思路。当然该方法在用于改变温度的情况下分析溶液的组成或计算溶解度方面还存在一定的局限,有待进一步完善。
1008-0546(2011)10-0091-02
G633.8
B
10.3969/j.issn.1008-0546.2011.10.046
