基于投影寻踪模型的水质综合评价
2011-04-19王暄
王 暄
(新疆巴州水利水电勘测设计院,新疆库尔勒 841000)
0 前言
水质评价是水环境管理和决策的重要组成部分。水质评价结果通常由多个非线性指标决定,仅依据某项指标得出的评价结论往往不相容,因此需建立多因素评价体系的水质评价模型。目前,关于水质评价方法主要有均值法[1]、灰色聚类法[2]、模糊综合评判法[3]、物元可拓法[4]等,从不同方面研究水质评价方法,各有优缺点。均值法忽略了各指标的重要程度的差异,灰色聚类法、模糊综合评判法、物元可拓法在指标权重获取方面受到样本容量的限制,因而对评价结果产生一定的影响。本文采用投影寻踪模型(Projection Pursuit Model,简称PPM),确定样本投影过程中的最佳投影方向并进行线性投影,客观确定各因子的权重,将高维数据转化为一维空间的综合投影值,从而实现水质的综合评价。
1 投影寻踪综合评价模型[5]
投影寻踪方法的基本思想是:利用计算机技术,把高维数据通过某种组合,投影到低维(1~3维)子空间上。然后通过优化投影指标函数,求出能反映原高维数据结构或特征的投影向量,在低维空间上对数据结构进行分析,以达到研究和分析高维数据的目的。其建模过程包括如下步骤:
(1)评价指标值的归一化
设研究方案集为:

其中:x*(i,j)为第i个方案第j个评价指标值;n,p分别为方案的数目和评价指标的数目。

对越小越优型评价指标可采用如下进行极值归一化处理:
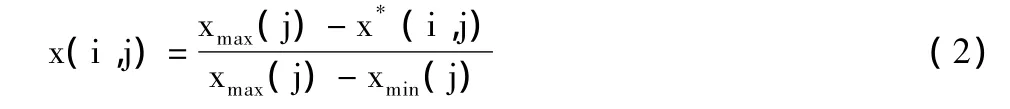
式中:xmin(j)、xmax(j)分别为方案集中第j个评价指标的最小值和最大值。通过式(1)和式(2)得到的x(i,j)统一为[0,1]区间上的评价指标。
(2)构造投影指标函数
PP模型就是把 p维数据 {x(i,j)|j=1,2,…,P}综合成以a=(a(1),a(2),…,a(p))为投影方向的一维投影值。
然后根据 {z(i)|i=1,2,…,n}的一维散布图进行方案优选,式(3)中a为单位长度向量。
在综合投影值时,要求投影值z(i)的散布特征应为:局部投影点尽可能密集,最好凝聚成若干个点团;而在整体上投影点团之间尽可能散开。基于此,投影指标函数可构造为:


式中:Sz为投影值z(i)的标准差,Dz为投影值z(i)的局部密度,即
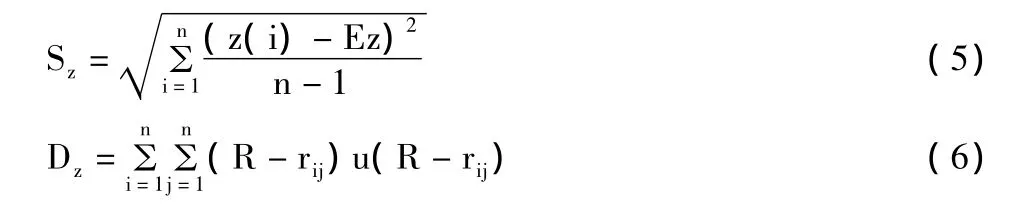
式中:Ez为系统 {z(i)|i=1,2,…,n}的均值;R为局部密度的窗口半径,它的选取既要使包含在窗口内的投影点的平均个数不能太少,避免滑动平均偏差太大,又不能使它随n的增大而增加太高,R可以根据试验来确定,一般可取值为0.1Sz;距离rij=|z(i)-z(j)|;u(R-rij)为为一单位阶跃函数,当t≥0时其函数值为1,当t<0时其函数值为0。
(3)优化投影指标函数
当方案集给定时,投影指标函数Q(a)只随投影方向a的变化而变化。不同的投影方向反映不同的数据结构特征,最佳投影方向就是最大可能暴露高维数据某类特征结构的投影方向。通过求解投影指标函数最大化问题可估计最佳投影方向,即:

这是一个以 {a(j)|j=1,2,…,P}为优化变量的复杂非线性优化问题,用常规优化方法处理较困难。模拟生物优胜劣汰规则与群体内部染色体信息交换机制的加速遗传算法是一种通用的全局优化方法,用它来求解上述问题十分简便和有效。
(4)分类
把由步骤3求得的最佳投影方向a*代入式(3)后即得各方案的投影值z*(i),显然z*(i)值越大对应的方案i越优。对z*(i)值从大到小排序,最大的z*(i)值所对应的方案i就是最优方案。
2 案例分析
本文运用投影寻踪模型,根据文献[6]数据,对河流水质进行综合评价。
2.1 评价指标的确定
根据该河流实际情况选择评价指标为:高锰酸盐指数(CODMn)、化学需氧量(COD)、氨氮(NH3-N)、挥发酚和总磷(TP)五个指标作为评价因子(见表1)。水质评价标准采用《地表水环境质量标准》(GB3838-2002)。各个采样点的污染指标实测值见表2。

表1 地表水水质分级标准 mg/L
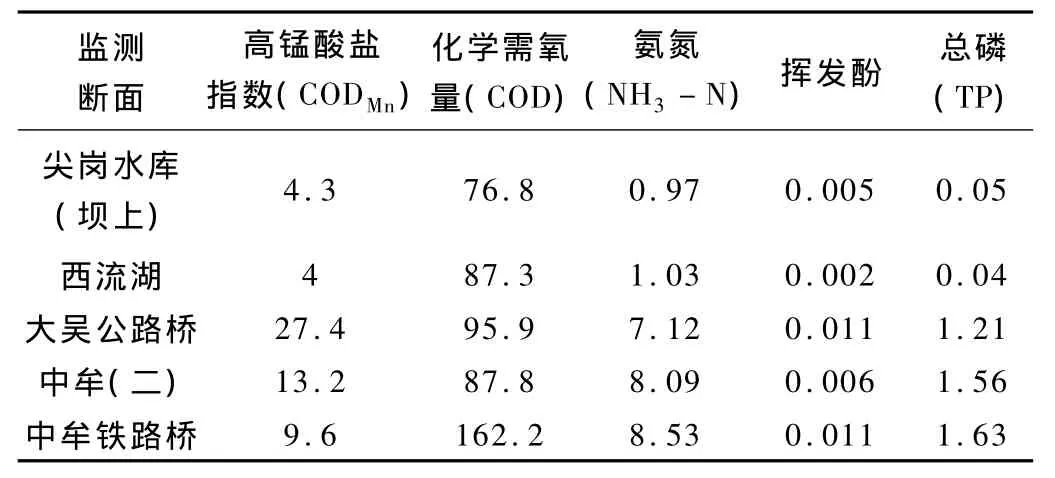
表2 贾鲁河主要污染物检测值 mg/L
2.2 问题的求解
根据(1)~(9)式,得出最佳投影方向:=(0.411 6,0.208 9,0.591 6,0.023 3,0.660 6),把分别乘以表3 中各指标优度值,即得各方案的投影值(见表3)以及水质类别临界点投影值(见表4)。

表3 各样本评价指标优度值

表4 水质类别临界点投影值
根据各监测断面的投影值可得水质的优劣排序(见表3),其评价结果与文献[6]的评价结果基本一致,但投影寻踪评价直接采取各样本的原始数据进行分析,结果更为合理。
3 结论
(1)将多维数据转化为一维指标值时,可能会造成部分数据之间所隐含信息的丢失,对结果产生一定的影响,因此应选择合适的数据处理方法。
(2)投影寻踪模型将指标体系(高维数据)投影到一维子空间上,建立投影寻踪模型,通过运算,寻找最佳投影方向,形成评价指标值,按大小进行排序。避免了模糊综合评判、理想解法等方法指标赋权的干扰,克服了传统方法的不足。
(3)最优投影值能够在一定程度上反映水体各评价指标影响程度的大小。同时,计算简单可行。模型准确反映了水体质量等级与投影值之间的非线性对应关系,等级划分界限清晰,为地表水质量评价研究领域提供了新的思路和方法。
[1]王娟,高原.水环境质量评价3种方法的应用对比[J].工业安全与环保,2007,33(2):16 -17,64.
[2]王洪梅,卢文细,辛光,等.灰色聚类法在地表水水质评价中的应用[J].节水灌溉,2007(5):20-22.
[3]仲少云,王庆,金秉福.模糊综合评判法在芝罘湾水质评价中的应用[J].海洋湖沼通报,2007(2):57-61.
[4]孙秀玲,马惠群,曹升乐.改进的可拓方法及其在水质评价中的应用[J].人民黄河,2006,28(7):30 -31,37.
[5]李祚泳.投影寻踪技术及其应用进展[J].自然杂志,1997,19(4):224-227.
[6]穆征,王方勇,李静,等.基于模糊综合评价模型的河流水质综合评价[J].水力发电,2009,35(4):11-13.
