残差灰色组合模型在建筑物变形分析中的应用
2011-04-19陈伟清陈佳佳田海涛
陈伟清,陈佳佳,田海涛
(1.广西大学土木建筑工程学院,广西南宁 530004; 2.桂林理工大学土木与建筑工程学院,广西桂林 541004;3.云南中正房屋测绘有限公司,云南昆明 650200)
残差灰色组合模型在建筑物变形分析中的应用
陈伟清1∗,陈佳佳2,田海涛3
(1.广西大学土木建筑工程学院,广西南宁 530004; 2.桂林理工大学土木与建筑工程学院,广西桂林 541004;3.云南中正房屋测绘有限公司,云南昆明 650200)
在传统灰色系统理论建模分析的基础上,将原始观测数据序列与所建模型预测数列进行比较,并将比较后的残差纳入系统,继续建立灰色模型进行分析。事实证明:在建筑物变形分析中使用残差灰色组合模型,能有效提高模型精度,获得良好的预测效果,是一种既方便又可靠的变形分析方法。
灰色系统;变形分析;残差灰色组合模型
随着20多年来灰色系统理论的巨大发展,许多科学和生产领域都开始应用灰色系统理论建模进行分析。工程方面的应用比较早的有大坝形变监测工作,目前在高层建筑物、构筑物的变形分析中也开始逐渐应用[1]。最普通的方法是对变形观测的原始累计数据建立灰色模型,并进行预测分析。如果一次建模分析后,对所得残差继续进行建模,与一次建模的结果共同组合,会收到良好的分析效果[2]。
1 灰色建模基本原理
1.1 GM(1,1)灰色模型
设初始数据序列为:
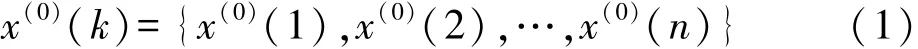
对(1)式作一次累加生成,得:
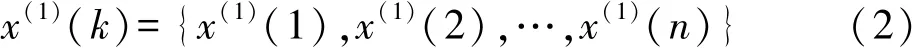
对式(2)建立一阶线性微分方程,称为模型的白化方程[3]:

其中,a为发展系数,b为灰色作用量。
根据最小二乘原理,GM(1,1)模型中的参数向量为[4]:
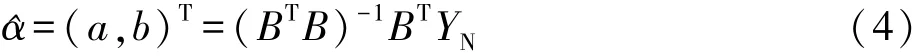
可解出发展系数a和灰色作用量b。
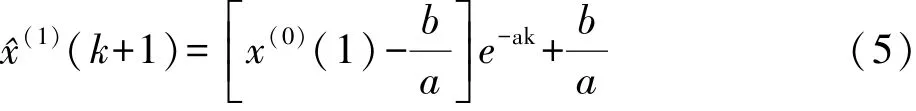
再作累减生成,可得模型的还原预测值[6]:
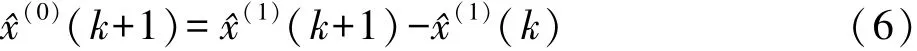
1.2 q-GM(1,1)残差灰色组合模型
由于单变量一阶灰色预测模型GM(1,1)的原始序列x(k)要求为非负数,因而在遇到变形数据为负数序列时,就需要进行转化。现采用直接将序列加一常数的平移变换方法,即使序列各项为正数,且经过平移变换还能提高模型精度。由于常数不同,所建模型序列的起始零点就不同,添加常数后使计算零点升高,预测值增大。因此,建模时应经过多次平移变换以得到最合理的预测模型[8]。
2 灰色模型精度检验的算法
灰色模型常采用后验差法进行精度检验。即以各点预测误差q(0)(k)为基础,检验后验差比值C和小误差概率P的大小,从而评定模型的精度[9]。残差值q(k)、后验差比值C和小误差概率P分别按下式计算:
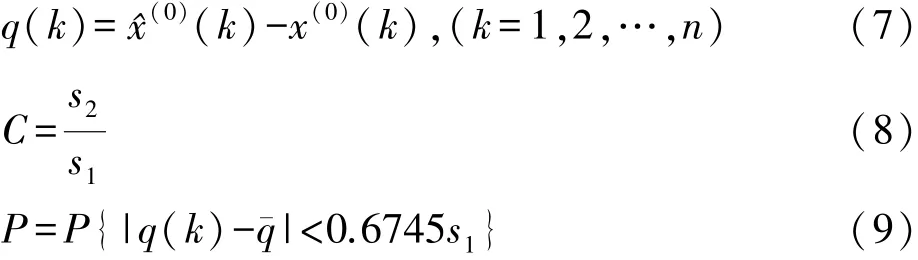
式中,s1为原始数列的标准差,s2为残差数列的标准差。C值越小,预测模型越好,P值越大,说明小误差的概率大,模型精度越高。各类精度等级的C、P值见表1[10]。
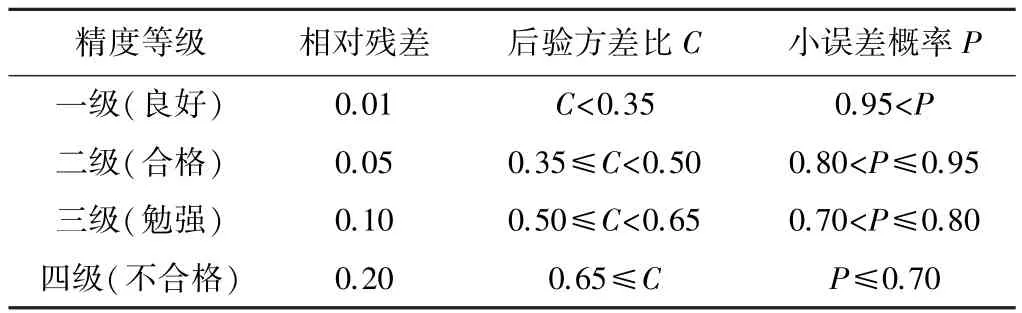
GM(1,1)模型精度检验标准 表1
3 残差灰色组合模型建立与应用分析
以某商务大厦的变形观测资料为例,表2为1号监测点位在各期的原始沉降数据,观测时间从2007年4月开始到2007年7月结束,历时90天。
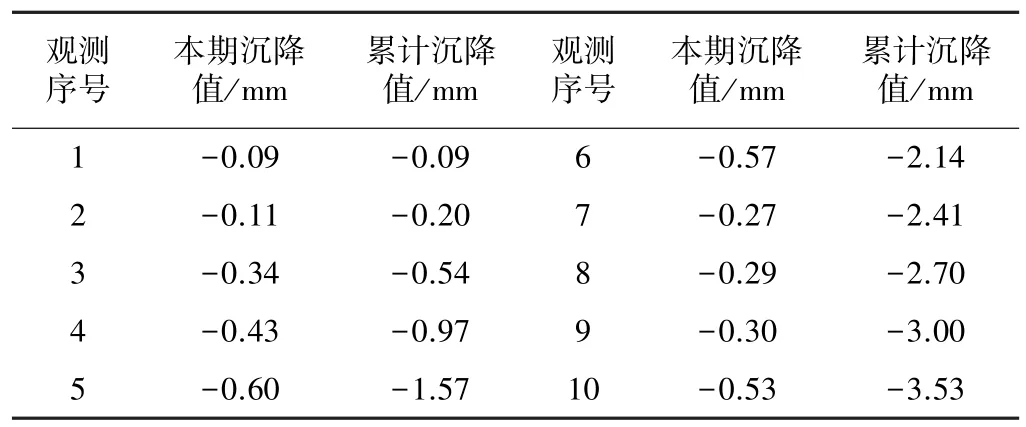
某商务大厦1号点位各期原始沉降数据 表2
3.1 GM(1,1)模型建立
选用表2中前7个周期的原始累计沉降值x(k)={x(1),x(2),…,x(7)}进行建模预测。为方便建模和计算,将x(k)直接平移10,得建模的初始序列x(0)(k),作一次累加生成x(1)(k)序列,由此建立GM (1,1)模型[11],经累减还原得累计沉降预测序列值(k),再计算出残差值q(k)和相对残差值ε(0)(k),计算结果如表3所示。
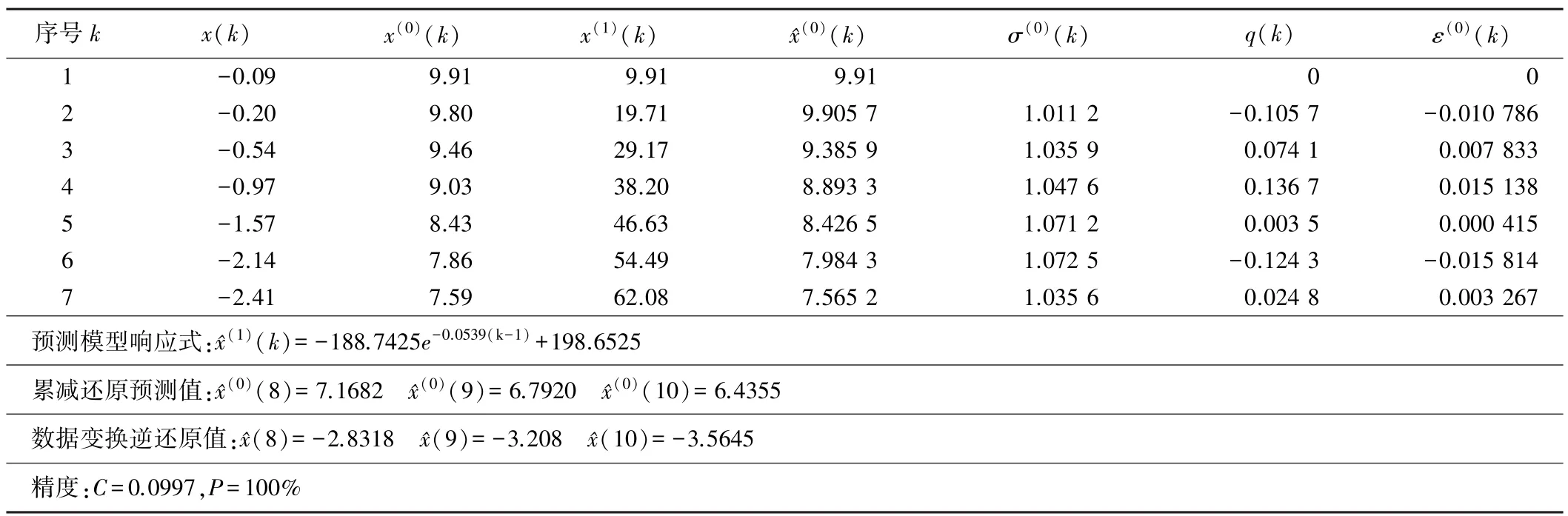
x(k)原始序列直接平移10的建模结果 表3
在表3中,后验差比C=0.099 7<0.35,小误差概率P=100%>95%,说明所建GM(1,1)模型良好,精度达到一级标准。
3.2 残差灰色组合模型建立与应用
(1)残差序列直接建模分析
取表3内第2-7期残差序列q(k)直接平移10得建模的初始数据序列q(0)(k),一次累加生成q(1)(k)序列,由此建立GM(1,1)模型,经累减还原得到残差预测序列值(k),再计算出q(k)的残差值q(0)q(k)和相对残差值ε(0)q(k)[12],结果如表4所示。
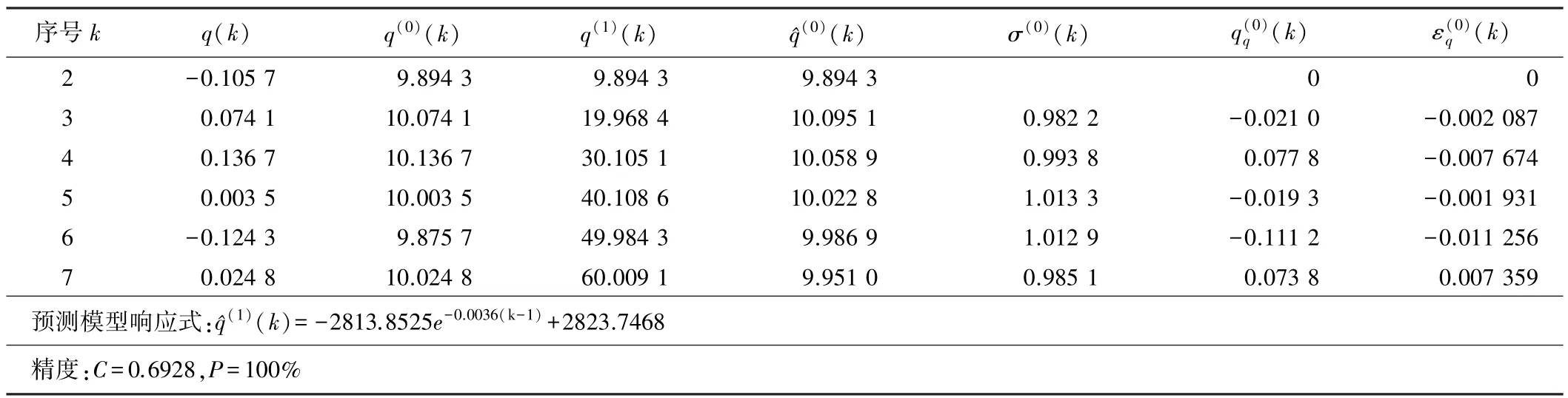
q(k)残差序列直接平移10的建模结果 表4
在表4中,残差模型的后验差比C>0.65,模型精度检验不合格,需要重新进行数据变换。同时发现,在使用原始数据序列x(k)和残差序列q(k)分别建模所计算的相对残差ε(0)(k)最大值均处在第6个周期。因此,可以分别将x(k)和q(k)中的第6个数据剔除后重新建模。此时,残差初始序列变为q(j),对该序列重新进行数据变换,分别直接平移50和100建立GM (1,1)模型,计算结果如表5所示。

q(j)分别直接平移50和100的建模预测结果 表5
从表5的结果可以看出,对残差序列q(k)剔除第6项后,分别直接平移50和100所建GM(1,1)模型的数据变换逆还原结果基本一致,后验差比和小概率误差均相同,0.35<C=0.449 9<0.50,P=100%,模型检验合格,精度为二级[13]。此时若再添加平移量建模,其结果对精度已无提高。
(2)残差序列组合建模与预测
从表4中可以看出,原始数据序列第6项为最大残差项,将x(k)剔除第6项后分别平移10和50建模并预测,其结果如表6所示。

x(k′)序列分别直接平移10和50的建模预测结果 表6
从以上平移变换的建模结果中可以看出,平移量不同所建立模型的参数不同,预测结果也不一样[14]。但是,对初始序列平移值的选择要根据需要来确定的,虽然平移值越大,相对残差变小,但有时也会出现预测还原值与实际值差异过大,因此不能一味追求小残差而选择大平移值。一般来说,在变形分析中对初始数据的平移变换值没有严格要求,通常以预测还原值与实际值最接近为基本原则,利用Matlab等计算工具经过反复试算,以确定合适的数据变换方法[15]。在表6中,初始数据直接平移10所建模型的预测还原值与实际值最接近。

残差灰色组合模型预测比对结果 表7
从以上数值可以看出,残差拟合值更加接近实测值。在建筑物变形分析中,采用第一次建模后所得残差与第一次建模结果共同组合继续建模,所获得的残差灰色组合模型适合进行短期预测,且预测效果良好。
4 结 论
在建筑物变形分析中,通过对原始序列建立GM (1,1)模型后继续分析残差,剔除相对残差太大的数据项,建立残差的GM(1,1)模型并进行预测,最后与原数据序列的GM(1,1)进行拟合,并通过平移变换的方法提高建模序列的起始零点,将序列变为非负,这种用q-GM(1,1)残差灰色组合模型对GM(1,1)灰色模型进行修正后的预测值,明显优于GM(1,1)模型,且模型精度基本上达到了一级标准。事实证明,q-GM (1,1)在建筑物变形分析中取得了良好的预测效果,是一种既方便又可靠的方法。
[1] 黄声享,尹晖,蒋证.变形监测数据处理[M].武汉:武汉大学出版社,2003.1:30~82
[2] 何秀凤.变形监测新方法及其应用[M].北京:科学出版社,2007:1~148
[3] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.2:210~278
[4] 邓聚龙.灰预测与灰决策[M].武汉:华中科技大学出版社,2002.9:45~109
[5] 刘思峰,谢乃明等编著.灰色系统理论及其应用[M].北京:科学出版社,2008:95~108
[6] 孙辰军,王翠茹,张江维等.残差灰色预测模型的改进与应用[J].统计与决策,2005(3):19~20
[7] 成永刚.灰色GM(1,1)模型预测精度的残差修正及对岩体变形预测的应用[J].四川建筑,2004(4):73~74
[8] 刘树,王燕,胡凤阁.对灰色预测模型残差问题的探讨[J].统计与决策,2008(1):9~11
[9] 陈伟清.灰色预测在建筑物沉降变形分析中的应用[J].测绘科学,2005(5):43~45
[10] 王亚飞,朱健,田海涛等.基于灰色线性回归组合模型的大坝形变监测数据处理和预测[J].内蒙古水利,2007 (1):91~92
[11] Chen Weiqing,Tian Haitao.The study Based on the MGM (1,n)Grey model to the building’s Deformation analysis [J].Advances in Management of Technology——Proceedings of The International Conference on Management of Technology,Taiyuan 2009:480~487
[12] 胡丽敏,黄长军,周新地.基于灰色残差GM(1,1)模型的建筑物沉降预测的研究[J].陕西理工学院学报(自然科学版),2009(9):37~40
[13] 付军,严新平,杨吉新等.基于灰色残差新陈代谢模型的悬臂施工主梁标高误差预测[J].武汉理工大学学报(交通科学与工程版),2009(8):627~630
[14] 张明远,傅礼铭,李跃.改进残差修正GM(1,1)模型在基础沉降预测中的应用[J].建筑科学,2007(11):67~70
[15] 刘棠洪,周俊,朱庆川.改进的灰色预测模型在地面沉降预测中的应[J].地质灾害与环境保护,2007(9):104~107
The Application of Residual Gray Combination Model in Building Deformation Analysis
Chen WeiQing1,Chen JiaJia2,Tian HaiTao3
(1.College of Civil and Architectural Engineering,Guangxi University,Nanning 530004,China;2.College of Civil and Construction Engineering,Guilin University of Technology,Guilin 541004,China;3.Housing Survey and Mapping Co.,Ltd.Zhongzheng 650200,China)
This paper analyzes the traditional model of gray system theory,based on the original observation data sequence and the model predicted the number of columns compared with the residual and more into the system after,continue to build the gray system model for analysis.Facts have proved:Using the residual gray combination model in the building distortion analysis,can improve effectively the accuracy of model,obtain good prediction,is a convenient and reliable method of deformation analysis.
grey system;deformation analysis;residual gray combination model
1672-8262(2010)03-99-04
TU196
A
2010—09—23
陈伟清(1964—),女,教授,主要从事工程测量、GIS应用研究。
广西自然科学基金项目(2010GXNSFA013002);广西教育厅科研项目(200808MS148)
