灰色预测在建筑物沉降变形分析中的应用

宋蕾，张俊中，张健雄

(1.河南省测绘工程院，河南郑州 450008； 2.河南省建筑科学研究院，河南郑州 450053；3.河南理工大学测绘与国土信息工程学院，河南焦作 454000)

灰色预测在建筑物沉降变形分析中的应用

宋蕾1∗，张俊中2，张健雄3

(1.河南省测绘工程院，河南郑州 450008； 2.河南省建筑科学研究院，河南郑州 450053；3.河南理工大学测绘与国土信息工程学院，河南焦作 454000)

通过对广州市某地产开发公司新建的居民楼沉降变形监测数据进行处理，分别建立传统的GM(1，1)模型和以相邻观测时间间隔为权直接生成1－WAGO非等间隔GM(1，1)模型，对两种模型进行分析与预报，比较的结果验证了1－WAGO非等间隔GM(1，1)模型在建筑物沉降变形分析中的实用性、正确性和有效性。

灰色系统；非等间隔；GM(1，1)模型；1－WAGO；变形分析和预测

1 引 言

对于建筑物，必须进行变形监测，分析与预报，用来指导施工和确保施工质量的一种理论依据，灰色系统理论用于建筑物的变形分析与预报是比较合适的理论体系。灰色理论GM(1，1)模型都是以等时间间隔(等步长)序列建模。在工程实践中，沉降变形观测资料一般都是以不等时间间隔的数据序列[1]，因此，须将等时间间隔序列的灰色理论模型推广到非等时间间隔序列。本文基于非等时间间隔建筑物的CJ1号点沉降观测数据为例，建立非等间隔GM(1，1)模型和以相邻观测时间间隔为权直接生成1－WAGO的序列模型，分别对建筑物的变形进行了分析与预报，比较的结果验证了1－WAGO灰色模型在建筑物沉降变形分析中的实用性、正确性和有效性。

2 非等间隔序列GM(1，1)模型的建立

灰色系统预测的基本思路是:把随时间变化的一随机正的数据序列，通过适当的方式累加，使之变成为非负递增的数据序列，并用适当的曲线逼近，以此曲线作为预测模型，对系统进行预测。

2.1 改进的非等间隔序列GM(1，1)模型[2]

当观测资料为非等间隔序列时，应先将非等间隔序列的原始观测资料变成等间隔序列，再以此为基础生成预测模型。

非等间隔GM模型有内插值改进法、二次参数拟合法、直接累加生成法等多种改进方法，本文采用单位时段差系数修正法形成非等间隔GM模型。

(1)判断观测周期为非等时间间隔

(2)T(0)(i)＝{t1，t2，…tn}，则平均时间间隔为:

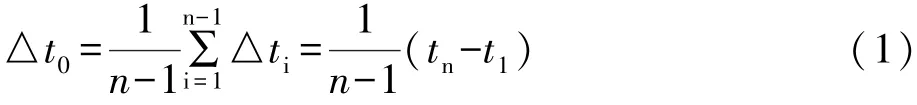
(3)各时段与平均时段的单位时段差系数μ(ti)为:

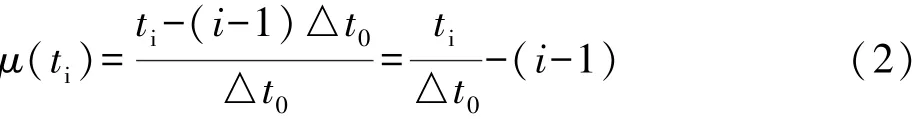
(4)则各时段总的差值为△x(0)(ti)

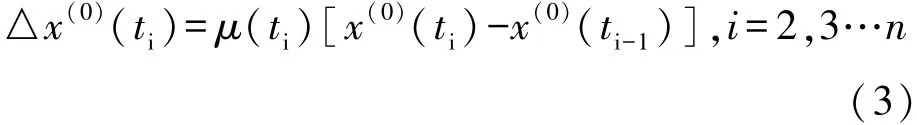
(5)各等间隔点的灰指数为:⊗i

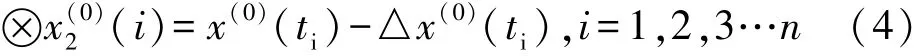
于是得到等间隔序列为:

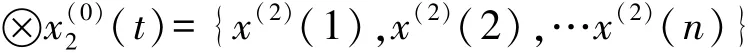
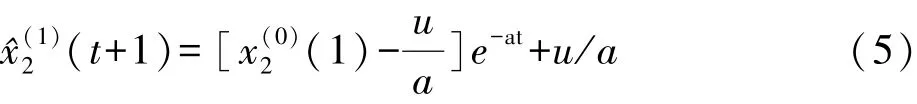
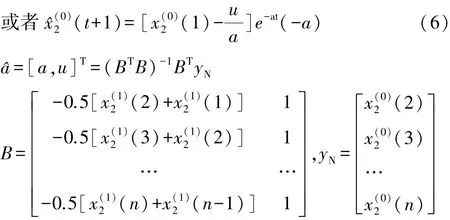
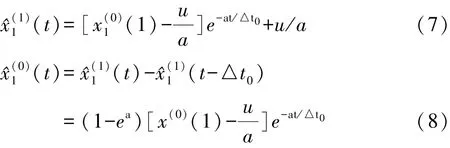
上式即为非等时空距的t时刻的灰色预测模型值。

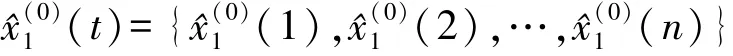
2.2 非等间隔序列GM(1，1)模型的精度检验

对模型精度即模型拟合程度评定的方法有残差大小检验、关联度检验和后验差检验三种。残差大小检验是对模型值和实际值的误差进行逐点检验；关联度检验是考察模型值与建模序列曲线的相似程度；后验差检验是对残差分布的统计特性进行检验，它由后验差比值C和小误差概率P共同描述。灰色模型的精度通常用后验差方法检验[3]。

即k时刻x(0)(k)与(k)之差为:

e(k)称为k时刻残差。记实际数据x(0)(k)，k＝1，2，3，…，n的平均值为:

记残差e(k)，k＝1，2，3，…，n的平均值为:

记原始数据(实际数据)的方差为:

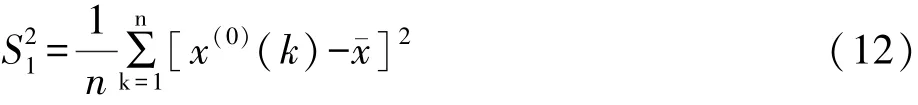
记残差方差为:

C称为后验差比值:

P为小概率事件:

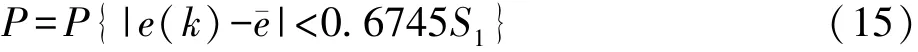
指标C越小越好，C越小，表示S1越大而S2越小。S1大，表示原始数据离散程度大。S2小，表示残差离散程度小。C小，表明尽管原始数据很离散，而模型所得计算值与实际值之差并不太离散。指标P越大越好，P越大，表明残差与残差平均值之差小于给定值0.6745S1的点较多。根据C与P两个指标，可综合评定模型精度。于是，模型的精度级别＝max{P所在的级别，C所在的级别}。表1为模型精度等级。

模型精度等级 表1

2.3 1－WAGO非等间隔序列GM(1，1)模型

针对数据非等间隔特点，还有以相邻观测时间间隔为权，作观测序列1－WAGO[4，5](Weight Accumulating Generation Operator)生成，直接建立非等间隔GM (1，l)模型。将GM(1，1)模型应用于建筑物的沉降观测分析与预报，应用表明该模型具有较好的实用性和较高的预报精度。

设ti时刻观测数据为x(0)(ti)，当相邻次观测时间间隔不等时，序列x(0)＝{x(0)(t1)，x(0)(t2)，…x(0)(tn)}称为非等间隔(步长)观测序列。对x(0)做一次1－WAGO[6]生成x(1)＝{x(1)(t1)，x(1)(t2)，…x(1)(tn)}，其中:

式中，a，u为参数。微分方程的解为:

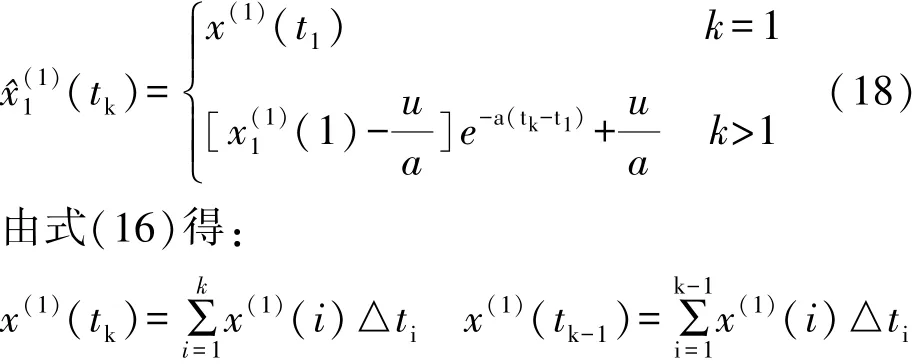
两式相减变换形式得差分还原公式为:

精度检验和上面的一样。

3 工程应用

本文所述的工程为广州市某地产开发公司新建的居民楼，依据有关规范[7]结合设计要求，在7栋居民楼布设28个沉降观测点。点号分别为(CJ1－CJ 28)。各沉降点埋设圆钢作为标志，该圆钢与居民楼连接在一起，伸出墙外5 cm～10 cm。水准工作基点布设在距该居民楼约20 m的地方，布设水准工作基点3个(BMI1－BMI3)，和广州市水利水电勘测设计院提供的珠基高程点N12、N9、N8、N7进行联测。每次施测时对其进行监测，以确定该基准点的稳定性。由工作基点BMI1作为起算点，进行联测。按照二等水准测量的要求进行往返测，对变形监测点进行了25期监测，观测精度均符合二等水准测量的技术要求，结果基准点稳定，可以进行数据的测量工作。

本文以建筑物的CJ1号点沉降观测数据为例，CJ1号的观测精度符合二等水准测量的要求，来说明传统GM(1，1)模型和1－WAGO非等间隔序列GM(1，1)模型在沉降观测中的应用。CJ1号点的部分观测值数据(备注:其他的高程值减去首次的高程值是“＋”值，代表建筑物下降)，如表2所示。

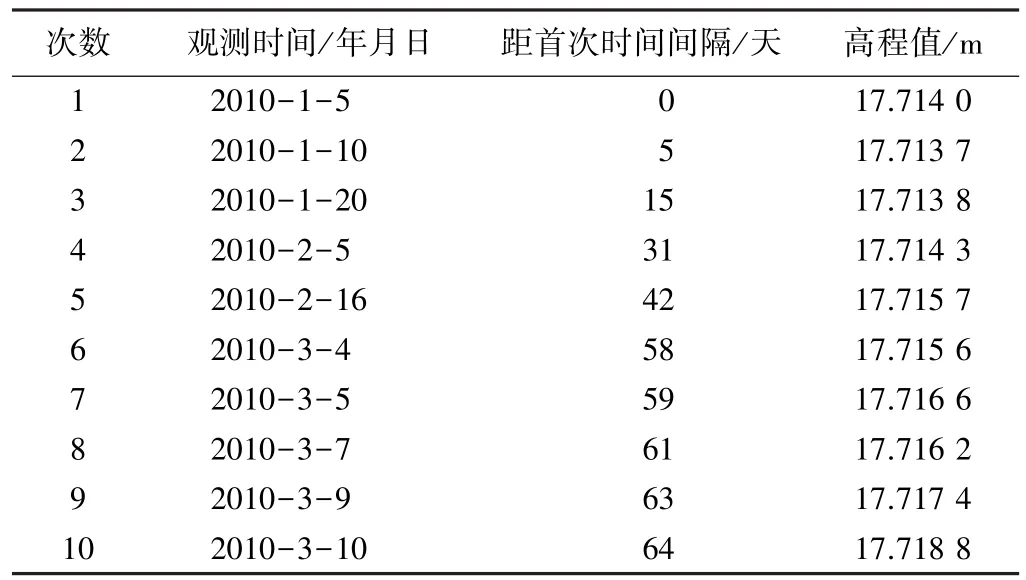
CJ1沉降观测点的部分资料 表2

3.1 数据计算

根据前面介绍的非等间隔数据建模的方法，利用10期的数据分别进行建模，为了进行数据的拟合和预测比较，两次的建模数据利用相同的观测高程值，采用两种方法进行建模，分别是传统的GM(1，1)和1－WAGO非等间隔序列GM(1，1)模型。

传统的建模过程如下:根据表2 CJ1在各个观测时段的高程值数据，利用表2中的10个数据，按照非等间隔序列建立预测模型，根据式(1)计算得到△t0＝7.11，利用式(2)～式(6)，其他的参数计算，如表3所示。

根据表3中的参数及计算公式

＝[a，u]T＝(BTB)－1BTyN＝[－0.00003393，17.711838]T，由此可以建立相应灰色微分方程的时间响应函数:

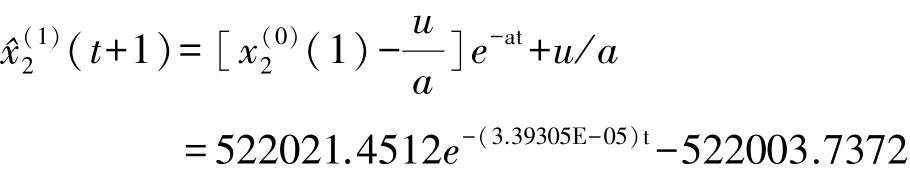
还原为非等间隔数列中与时间t有关的响应函数:

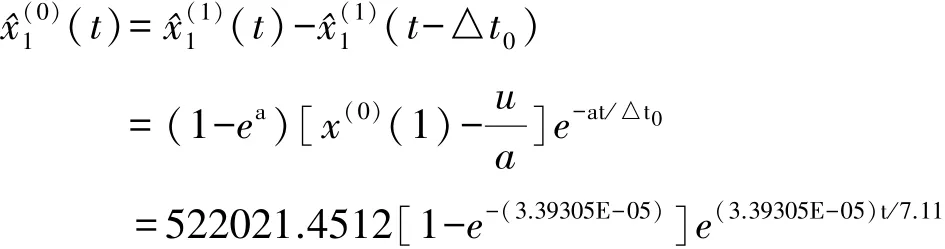
1－WAGO非等间隔模型建模过程如下:根据表2 CJ1在各个观测时段的高程值数据，利用表2中的10个数据，按照相邻观测时间间隔为权，作观测序列1－WAGO生成，直接建立非等间隔GM(1，l)模型。根据式(17)计算△t＝{1，5，10，16，11，16，1，2，2，1}，原始的观测序列x(0)的1－WAGO的序列x(1)的紧邻均值生成序列:

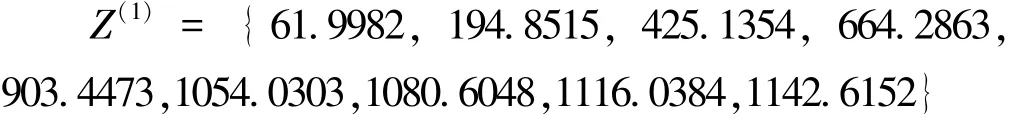
根据Z(1)计算出参数a、u的最小二乘解为:

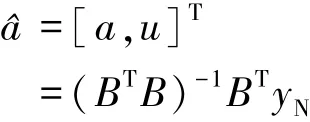
最终建立的预测方程为:

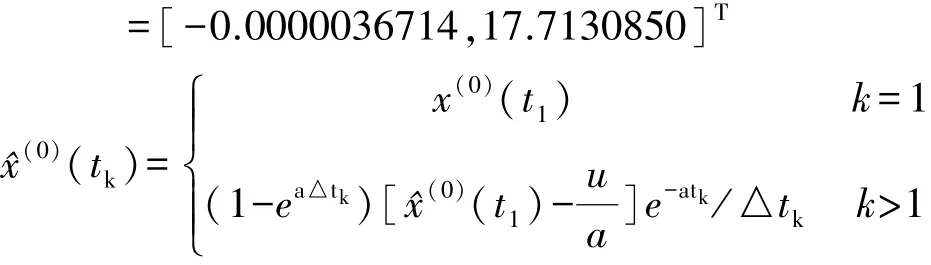
表4是传统的GM(1，1)模型和1－WAGO非等间隔GM(1，1)模型的拟合结果，表5是传统的GM(1，1)模型和1－WAGO非等间隔GM(1，1)模型的预测结果。

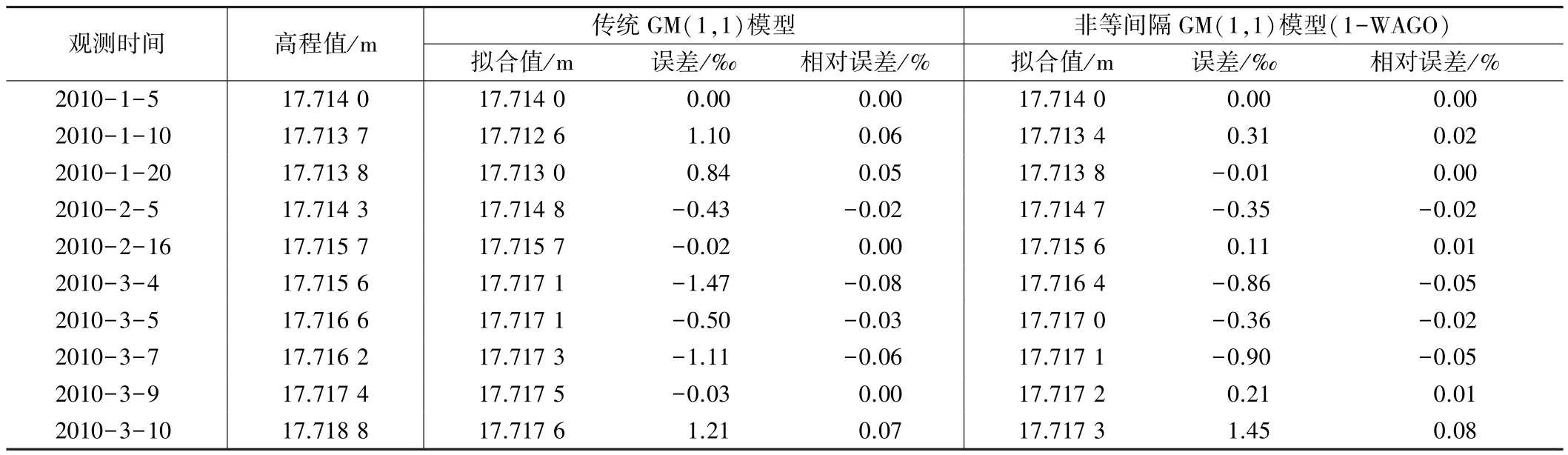
两种模型拟合结果 表4

3.2 灰色模型精度分析和灰色预测

从表4可以看出，传统模型拟合平均误差为0.847 2 mm，后验差比值C＝0.459 5，非等间隔模型(1－WAGO)拟合平均误差为0.635 8 mm，后验差比值C＝0.427 8，这说明两种模型拟合的精度和可靠性差别不是太大。

两种模型预测结果 表5

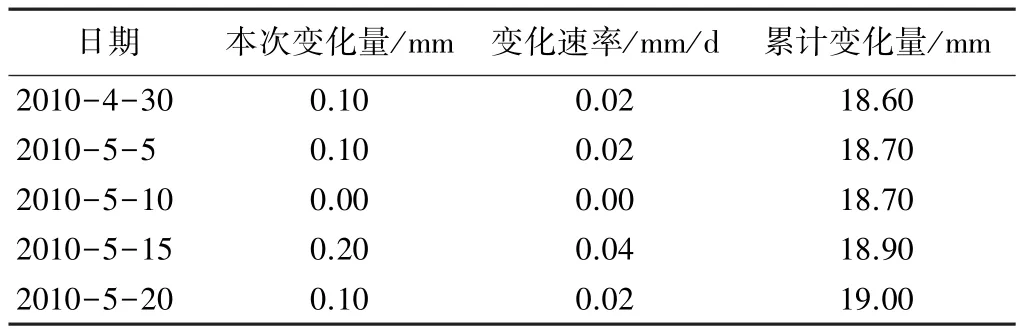
最后五次的高程变化量 表6

4 结 语

通过上述实例计算分析可见，通过非等间隔时间的10个监测数据进行建模，模型精度均为2级。依此模型对后续5个观测时间的高程值进行预测，其预测值和实测值也是非常接近，相对误差较小，说明模型的质量比较好，表明了非等间隔模型(1－WAGO)的模型可靠性强，精度较高。影响建筑物沉降的因素较多，模型建立难度较大，将灰色理论及灰色模型预报技术应用于变形监测点沉降预报的研究结果表明，精度很高，采用GM模型预报沉降变形监测预报结果能够满足要求。本文参考一些相关的资料所建立的1－WAGO灰色模型预测模型，计算步骤简单，直接省去了把非等间隔时间化为等间隔时间，工程实例应用表明，1－WAGO灰色模型预测精度比传统的模型预测精度高，所建立的预测模型具有较好的可靠性和可行性。

[1] 刘明波，田亚林，孙和平.非等步长GM(1，1)模型及其在大堤沉降监测的应用[J].测绘工程，2006，15(3):58～60

[2] 黄生享，尹辉.变形检测数据处理.[M].武汉:武汉大学出版社，2003，108～109

[3] 汪祖名.高速公路软土地基沉降变形监测分析与预报[J].苏州科技学院学报(工程技术版)，2004，17(2):34～40

[4] 龚建伍.建筑物变形监测及安全评价方法研究[D].武汉:武汉大学，2004

[5] 齐长鑫，汪树玉.灰色系统模型在坝基位移预测中的应用[J].水利学报，1996，9(5):49～52

[6] 蓝悦明，王新洲.灰色预测用于大坝变形预测的研究[J].武汉测绘科技大学报，1996，21(5):350～354

[7] GB 50026－2007.工程测量规范[S].

Application of Gray Forecast in the Deformation Analysis of Building

Song Lei1，Zhang JunZhong2，Zhang JianXiong3
(1.Surveying and mapping academy of engineering HeNan，Zhengzhou 450008，China；2.HeNan provincial academy of building research，Zhengzhou 450053，China；3.School of surveying and land information engineering of He Nan Polytechnic University，Jiaozuo 454000，China)

Through a real estate development company in Guangzhou City，the new residential building settlement monitoring data processing.It has respectively applied for the traditional GM(1，1)model and the adjacent observation time intervals to the right to directly generate 1－WAGO non－interval GM(1，1)model，Which have carried on the analysis and the forecast to two kind of models.The result verifies the 1－WAGO non－interval GM(1，1)model in building in the settlement of practicality，accuracy and effectiveness.

gray systems；non－interval；GM(1，1)model；1－WAGO model；analysis and forecasting of deformation

1672－8262(2010)03－94－05

TU196.2

B

2010—09—18

宋蕾(1984—)，女，助理工程师，研究方向:变形监测和数据处理。

河南省重点科技攻关项目(0302032700)