缓和曲线加宽段路幅边缘线长度的计算
2011-04-18王景海刘春彦
王景海,刘春彦
(1.北京市门头沟区住房和城乡建设委员会,北京 102300; 2.北京市市政一建设工程有限责任公司,北京 100083)
缓和曲线加宽段路幅边缘线长度的计算
王景海1∗,刘春彦2
(1.北京市门头沟区住房和城乡建设委员会,北京 102300; 2.北京市市政一建设工程有限责任公司,北京 100083)
推导出缓和曲线加宽段路幅边缘线长度计算的数值积分表达式,指出现有文献计算公式错误之处,澄清了错误认识。给出了卡西欧fx-4800P计算器程序及步长自适应验证程序清单,结合工程实例,验证所推公式正确性。
缓和曲线;边缘线;长度计算;程序;算例
1 引 言
公路路线设计规范规定[1]:当平曲线半径等于或小于250m时,路面内侧应加宽,路基也随之加宽。加宽过渡的设置根据道路性质和等级可采用不同的方法,比例加宽过渡法和高次抛物线加宽过渡法是常采用的方法。
加宽过渡后,求取道路缓和曲线段内侧路幅边缘线的长度,不但具有理论上的意义,而且也有着实际应用的价值,如计算、放样、计量位于该部分工程构筑物问题就涉及需先知道该部分长度。文献[2,3]分别就采用比例加宽过渡法和高次抛物线加宽过渡法两种情况下内侧路幅边缘线长度计算公式进行了推导,得出了加宽段边缘线长度计算公式。但在公式推导时由于把加宽边缘线长度微元与转角微元、半径之间关系式列立错误,从而导致了边缘线长度计算公式的错误。该公式在缓和曲线段长度较长、圆曲线半径较大、加宽值不大时误差尚不明显,但在缓和曲线段长度较短、圆曲线半径较小、加宽值较大时误差明显。本文由路幅边缘线坐标参数方程入手,根据微积分中参数方程弧长公式,得出路幅边缘线长度计算积分表达式,分析了现有文献的错误与不足,给出了卡西欧fx-4800P计算器程序及步长自适应验证程序,又结合工程实例,验证了公式的正确性。
2 公式推导
由于高等级道路一般仅在内侧加宽,所以本文仅讨论内侧路幅加宽边缘线长度计算问题。
建立如图1所示的独立坐标系。缓和曲线全长L0,缓和曲线参数为A,圆曲线半径R,半幅路宽D,全加宽W。
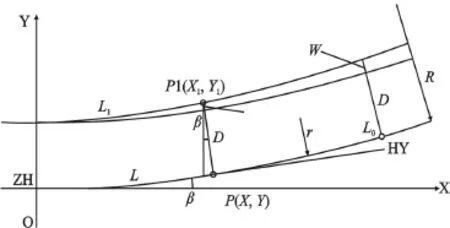
图1 中线、加宽边缘线关系图
中线长度L处点P(X,Y)对应路幅加宽边缘线处点P1(X1,Y1)的加宽值为Wx,则针对线性与高次抛物线加宽两种形式,Wx的表达式分别为:
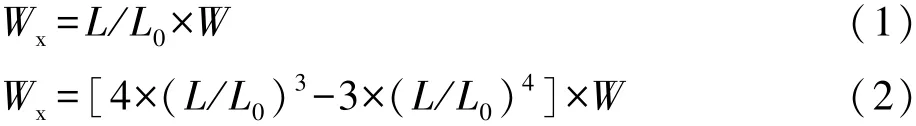
中线点P(X,Y)、路幅加宽边缘线处点P1(X1,Y1)坐标有如下关系[1]:
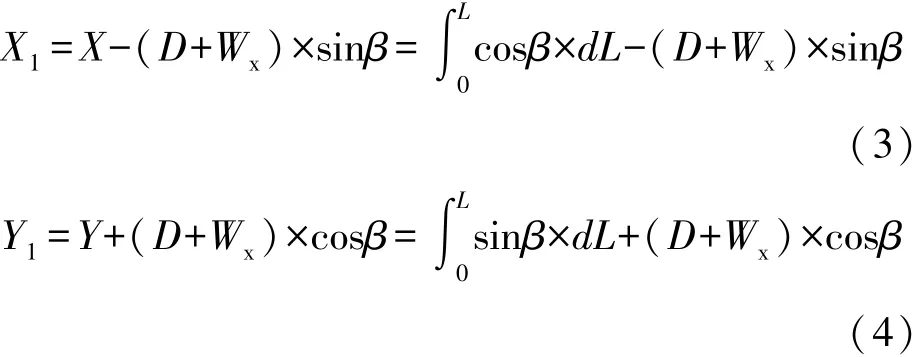
式中β为缓和曲线转角,β=L2/2A2
式(3)、式(4)分别对L求导得:
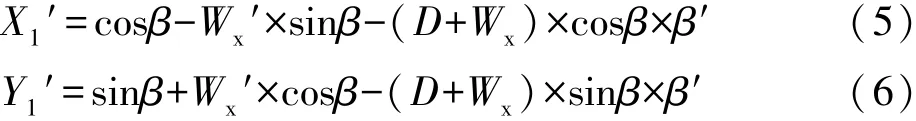
由微积分中参数方程弧长公式,路幅边缘线长度L1的表达式为:
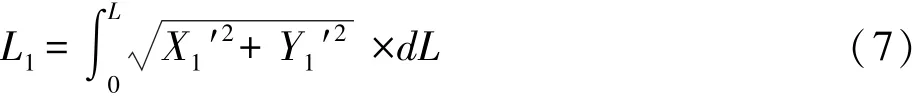
将式(5)、式(6)代入式(7)并整理得:
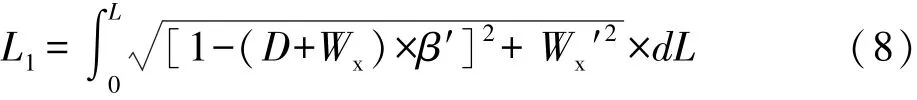
式(8)即为路幅边缘线长度精确计算之积分表达式。当全加宽值W=0时,Wx=0,式(8)即变为等宽时内侧边线计算公式[4]:
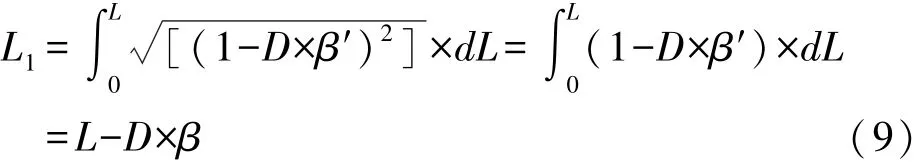
3 现有文献错误与不足之处
文献[2,3]都犯了同样一个错误,即都认为加宽边缘线长度微元dL1与转角微元dβ、半径之间存在如下关系:

实际上式(10)是错误的,因为中心线上任一点的法线与加宽边缘线并不垂直,法线仅与中心线或等宽边线垂直,因而式(10)等式关系并不成立,在此基础上导出的边缘线长度计算公式必然是错误的。
文献[5]给出的是边缘线长度计算的近似公式,该公式与加宽边线方程式没有实质上的联系,在理论上缺陷是明显的,只能作为近似的公式使用。
4 卡西欧fx-4800P计算器程序及验证程序
卡西欧fx-4800p计算器是日本卡西欧公司生产的一种科学计算器,它除了具有一般科学计算功能外,还具有数值积分计算和程序功能。它利用复化辛普生法进行数值积分计算,且有4500字节的数据存储容量,可满足一般工程测量计算需要。
路幅边缘线长度精确计算式(8)为数值积分表达式,无法求得其原函数,不能用牛顿-莱布尼茨公式求解,但可以利用卡西欧fx-4800p计算器的数值积分计算功能对其进行求解计算。
验证方法采用以弦代曲方法。具体说就把曲线分成适当长度的小段,若每段弧长与弦长之差小于一给定小值,则可以以弦长代替弧长。由于加宽段路幅边缘线曲率半径大于相应的圆曲线段曲率半径,因此若圆曲线段给定弧长与弦长之差小于一给定小值,则以该给定弧长均分加宽缓和段中线,得到每个均分点对应的路幅边缘线点坐标,将相邻点间的弦线长度累加求和,即可作为路幅边缘线的实际长度。
如图2所示,设圆曲线半径为R,圆心角为α,相应的弧长为L,弦长为C,则弧长与弦长之差为:
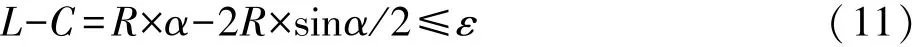
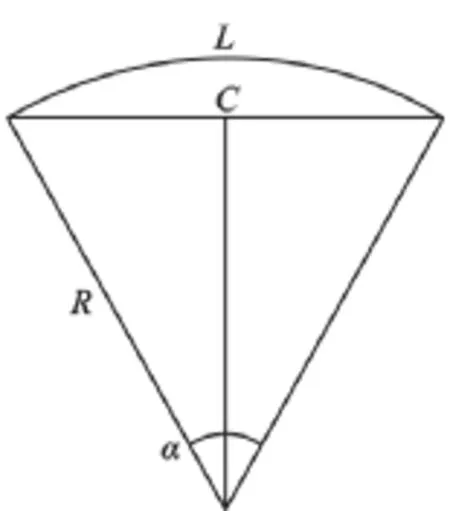
图2 弧长与弦线关系图
将sinα/2展开,略去高次项并顾及α=L/R,代入式(11)整理得:

取ε=0.001,代入(12)式得:

即当加宽缓和段中线上分段长度满足式(13),对应的路幅边缘线上相邻点一定满足以弦代曲要求。
程序清单:


该程序将线性与高次抛物线加宽两种形式的路幅边缘线长度计算统一到一个主程序中,自适应步长验证程序作为子程序供主程序调用。
运行主程序,输入缓和曲线全长L0,中心线长度L,半幅路宽D,全加宽W,缓和曲线参数A,中心线圆曲线半径R,提示选择加宽形式:o=1表示选择线性加宽,o=2表示选择高次抛物线加宽,选择1或2输入,程序显示出路幅边缘线长度计算结果L1,按回车键显示出验证计算结果L2。
5 工程算例
先举文献[2]中算例。路幅边缘线按线性加宽,L0=200 m,D=12.25 m,A=300,R=450 m,全加宽W值分别按0.75 m,1.25 m,1.75 m,2.5 m计算。按数值积分法、以弦代曲法验证及文献[2,5]计算结果如表1所示。
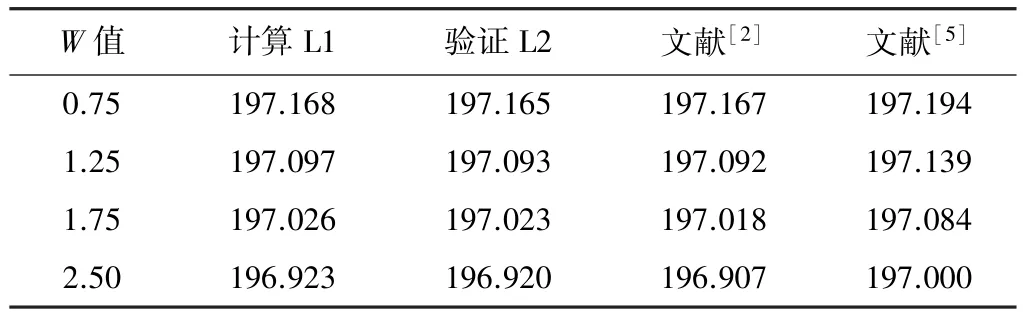
线性加宽计算结果(单位/m) 表1
若按高次抛物线加宽,则数值积分法、以弦代曲法验证及文献[5]计算结果如表2所示。
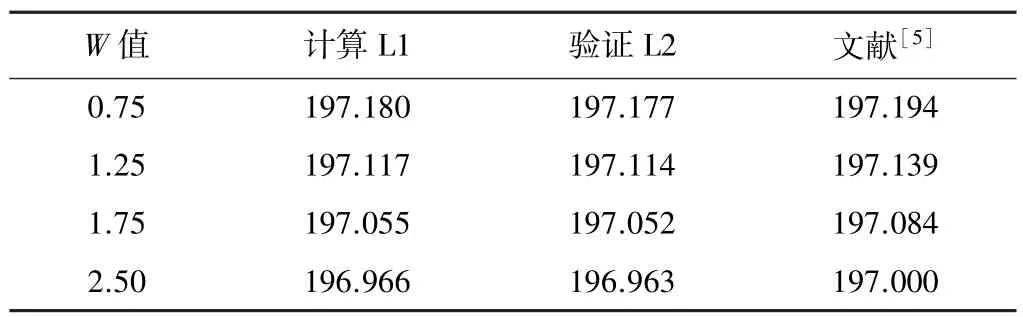
高次抛物线加宽计算结果(单位/m) 表2
再举文献[5]中算例。路幅边缘线按线性加宽,L0=50 m,D=6.0 m,A=66.332,R=88 m,全加宽W值分别按0.75 m,1.25 m,1.75 m,2.5 m计算。按数值积分法、以弦代曲法验证及文献[2,5]计算结果如表3所示。
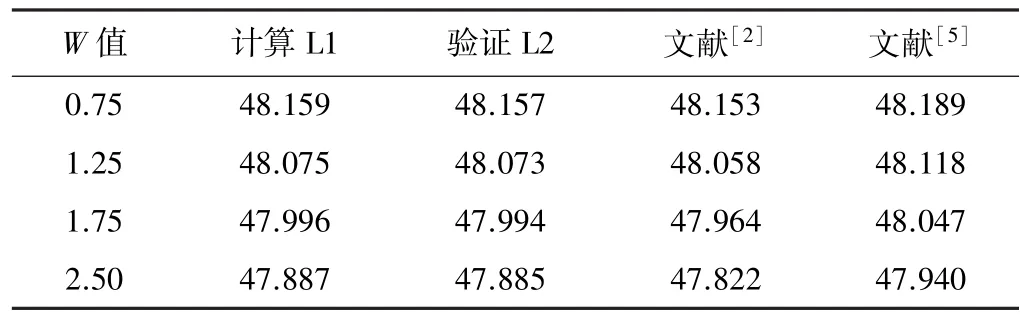
线性加宽计算结果(单位/m) 表3
表1~表3中验证计算结果L2与计算结果L1之差别可以认为是以弦代曲误差所引起。表1、表3中文献[2]部分结果虽然与计算结果也很接近,是因为算例中或缓和曲线段长度较长、或圆曲线半径较大、或加宽值不大的缘故,不能就此认为文献[2]所给公式正确。由上表也可看出,当缓和曲线段长度较短、或圆曲线半径较小、或加宽值较大时文献[5]的近似计算误差也较大。
6 结 语
本文所推导的缓和曲线加宽段路幅边缘线长度计算公式及相应的程序,可以广泛应用到位于该部位构筑物的计算、放样与工程量计量工作中。
[1] 张志清.道路勘测设计[M].北京:科学出版社,2005
[2] 赵新华,杨金保,丁伟.关于缓和曲线段路幅边缘线长度的精确计算[J].交通科技,2008(5):38~39
[3] 陈翠丽,丁建明.缓和曲线加宽内外边线的计算方法[J].交通标准化,2006(9):104~106
[4] 王景海.道路平曲线平行线弧长通用公式及应用[J].城市勘测,2009(2):121~123
[5] 彭飞,刘齐军.平曲线加宽缓和段内侧边线长度的近似计算[J].工程勘察,2008(1):66~68
The Calculation of Widend Sideline Length for Transition Curve Route
Wang JingHai1,Liu ChunYan2
(1.Beijing Mentougou District Municipal Commission of Housing and Urban-Rural Development,Beijing 102300,China;2.Beijing No.1 Municipal Construction Engineering Co.,Ltd.Beijing 100083,China)
The paper deduced the numerical integration calculation formula of widend sideline length for transition curve route and analysed the existent documents′error and shortage,then the the Casio-fx 4800p computer program、step-size proved program and engineering examples are also be given respectively.
Transition curve;Sideline;Length calculation;Program;Example
1672-8262(2011)02-150-03
P209,P258
B
2010—07—13
王景海(1970—),男,高级工程师,主要从事工程测量技术与管理工作。
