超声流量计探头对流场及其测量性能影响研究

张朋勇,郑丹丹,徐天室,张力新,胡鹤鸣

(1.天津大学电气与自动化工程学院,天津 300072;2.唐山汇中仪表有限公司,河北唐山 063020;3.中国计量科学研究院,北京100013)

0 引 言

超声流量计近10年发展迅速,与传统流量计相比,具有无压力损失,测量范围宽、重复性高等优点,且具有较高的测量精度。目前,多声道超声流量计广泛应用于国内外大型水电站输水管道的流量计量,以实现水轮机效率和状态的在线监测[1]。此外,美国、荷兰等12个国家已将多声道超声流量计应用于天然气贸易输送计量[2]。我国在“西气东输”工程中,也正在研究用超声流量计取代传统的孔板流量计达到准确计量、节能降耗的目的[3]。

但在实际应用中发现,为了避免输送介质时管道中的杂质、管衬、结垢、沉淀物等遮住探头,影响探头收发信号,一般会将探头插入管内。以往学者对该问题进行了研究。杉下钟尾[4]根据管道内流体理论速度分布公式,选取探头间的流速分布进行数值积分得到各声道线平均速度,由此求得的声道线平均速度偏大,导致测量误差均为正值。作者虽然考虑到探头插入管内使声道长度缩短,但是忽略了探头对流场的影响。此外,探头形状及其插入深度不同对流场的影响也不同,也会对测量误差造成影响。A.Voser[5-6]对ACCUSONIC公司的7600型超声流量计进行研究,指出探头对测量误差的影响随着管径增大而逐渐减小。T.Staubli,T.T resch[7]对RITTMEYER公司的一款Risonic型超声流量计进行研究,指出探头对测量误差的影响与雷诺数、管壁粗糙度有关。

实际上由于探头的存在,势必会使管道内尤其是探头附近的流场产生变化,而超声流量计测得的体积流量与各声道上的速度分布密切相关。因此,探头附近流场的变化将直接影响测量结果。拟采用Fluent流体力学数值仿真软件对这一问题展开研究,讨论超声探头在一种典型安装方式时,探头对超声流量计测量性能的影响规律。在此基础上,通过流场分析,揭示探头对流场的影响机理,从而解释分析仿真结果。

1 多声道超声流量计工作原理

多声道超声流量计的工作原理如图1所示,分别为其前视图和侧视图。在被测管道上设置n个(单测量断面A或B)或2n个(双测量断面A和B)平行测量声道,声道位置按照Gauss-Jacobi积分方法[8-10]布置,求取每个声道上的线平均流速,进而利用Gauss-Jacobi权系数加权计算出面平均流速和流量。

图1 多声道超声流量计原理图Fig.1 Sketch of multi-path ultrasonic flowmeter

图1中,“o”表示超声探头。对于单个测量断面(声道1～n为A测量断面,声道n+1～2n为B测量断面)有

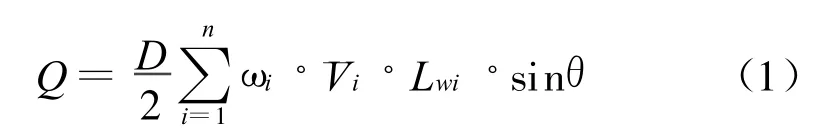
式中：Q-体积流量;D-管道内径;¯Vi-声道i上发射探头与接收探头之间的线平均速度;θi-声道i与管道轴心的夹角,称为声路角;ωi-声道i的权重系数;Lwi-声道i的理论长度,即管道内壁到内壁之间的距离。

图1中,Ψ-旋转角,即声道在yoz平面的投影与z轴正方向之间的夹角;di-声道i到管道轴线之间的距离,i=1、2、…、2n。

对于双断面测量来说,取两个断面测量体积流量的平均值即为最终的流量值。(下文中“声道”均表示“实际声道,即声道上发射探头和接收探头之间的范围”)。

工业上常用的超声流量计多是基于时差法测量原理,各声道的线平均速度通过测量时差反映。由于Fluent仿真方法无法引入声波传播时间,因此各声道线平均流速均采用对声道上各节点速度进行线积分的方法得到。如图2所示,流动为 x方向,管道直径为D,声道ab与x、y、z轴正方向夹角分别为α、β、γ,有

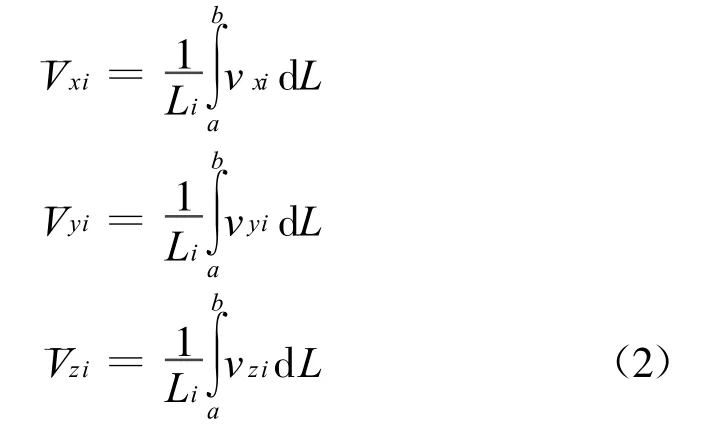
将式(3)代入式(1)即可得到仿真的管道流量。

探头插入到管道内部会缩短声道长度,影响流场。由式(2)、(3)可以推断,各声道线平均速度将受到影响。再由(1)式可知,Q值也将受到影响,从而造成测量误差。因此,拟采用数值仿真方法研究超声流量计探头对流场及其测量性能的影响。

图2 声道夹角示意图Fig.2 Sketch of path angle

2 数值仿真

所采用的仿真模型是基于唐山汇中仪表有限公司的一台DN500交叉9声道超声流量计建立的,如图3所示。声道位置及权重系数按照Gauss-Jacobi积分方法确定,如表1所示。为了准确建模,又对该流量计关键尺寸进行了测量,其实际口径为500.023mm,声路角为44.918°,旋转角为0°。

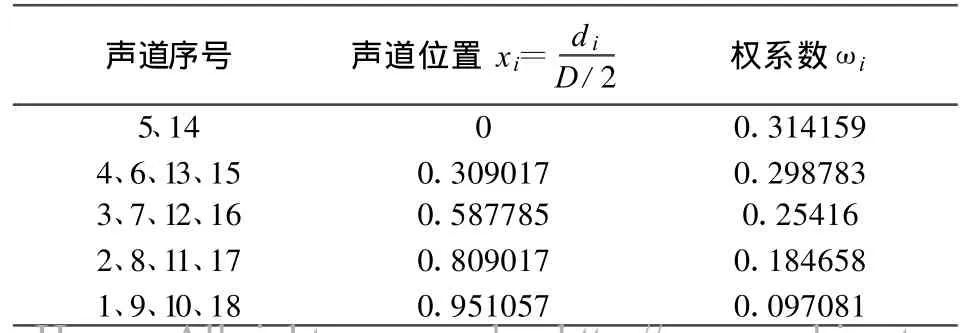
表1 声道位置及权重系数Table 1 Path position and path weight

图3 探头全伸安装的交叉9声道超声流量Fig.3 Ultrasonic flowmeter whose probes are fully inserted into the interior of a channel

该超声流量计采用圆柱形探头,直径为12mm,探头全伸位置安装,即探头前端面全部伸入到管道内壁,且前端面与管道内壁相切,如图4所示。

图4 探头全伸位置安装的示意图(局部)Fig.4 Sketch of probes fully inserted into the interior of a channel(partial)

在应用Fluent进行数值仿真前,必须建立研究对象的几何模型,并对其进行网格划分。使用Gambit前处理软件进行几何建模和网格划分。实验管道为直管,管道直径D=500.023mm,总长度为L= 15D。为了方便网格划分,将直管分为3部分：测量段(即超声流量计安装位置)、上游9.4D、下游4.4D,如图5所示。网格划分如下：

(1)前、后直管段：为圆柱体,形状规则,因此采用六面体网格。由于靠近管壁处速度梯度较大,因此需要对壁面附近网格进行局部加密,采用了边界层网格,按照First Row(第一层网格尺寸)、Growth Factor(尺寸增长因子)、Rows(层数)依次为1、1.1、15进行设置;

(2)测量段：由于探头的存在,该部分模型结构复杂。因此,选用四面体网格,并且采用增长函数画法,以18对超声探头的表面为增长源面进行网格划分,Start size(起始网格尺寸)、Growth rate(尺寸增长因子)、Size limit(最大网格尺寸)分别为1、1.1、10。如图6所示,这种划分方法既可以保证探头附近网格足够密,又可以控制网格数量。

最终,整个模型的网格总数量为771万。

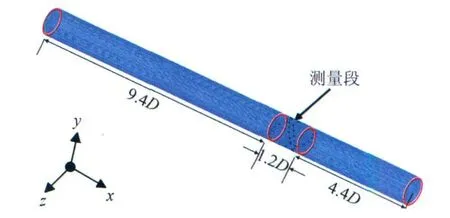
图5 模型尺寸示意图Fig.5 Sketch of the simulation model

图6 模型网格划分图(局部)Fig.6 CFD mesh of the simulation model(partial)

完成建模和网格划分后,将网格文件导入Fluent软件进行仿真计算,采用均匀速度入口,出口设为outflow,体与体之间连接面采用interface,介质为水,速度压力耦合采用SIMPLEC算法,湍流模型为雷诺应力模型(RSM)[11],壁面光滑。

3 仿真结果分析与讨论

确定了仿真方法后,对上述超声流量计的测量性能进行研究,讨论同一口径D、不同入口流速Vin条件下,插入管道内部的探头对流场及超声流量计测量性能的影响。

定义测量误差ε

其中,Qt-理论流量,对于仿真来说由式(5)得到,对于实验来说由标准表得到;Vin-仿真中设置的入口速度;S-管道横截面积;Q-超声流量计测得的体积流量。

3.1 仿真与实验结果对比

分别对口径D=0.500023m的超声流量计在不同流速(不同Re)下的5种情况进行仿真研究。为了验证仿真方法的准确性和可行性,与唐山汇中仪表有限公司提供的3组实验数据进行比较,见表2中①、②、③,入口速度均为实验中标准表测得的流速值。仿真结果与实验结果如表2。

由表2中①、②、③,比较仿真结果和实验结果可知：在相同流速下,两者的测量误差ε最大相差仅为0.16%,而且两者的变化趋势一致。说明仿真能够很好地反映实验结果,可以作为研究探头对流场影响的重要手段。

表2 仿真与实验结果对比Table 2 Comparison between results of simulation and experiment

由上表中仿真结果可得出如下规律：

(1)探头全伸安装、入口速度为0.3～8m/s时,测量误差ε总是为负;

(2)相同口径条件下,随着入口速度增大(即Re增大),测量误差有逐渐增大的趋势;当入口速度(或Re)达到一定范围时,测量误差基本不变。

3.2 仿真结果分析

3.2.1 探头对流场的影响

由于所研究的模型成轴对称结构,且对称声道的速度分布几乎完全重合。因此,只对1～5声道上的速度分布进行分析。

(1)测量段流体受探头的影响,会在探头附近产生回流(如图7);而靠近上游的探头附近所产生回流正好经过测量声道,即在探头附近产生负速度(如图8)。

图7 声道1和声道10所在平面的轴向速度云图(局部)Fig.7 Axial velocity contour in the plane with path 1 and path 10

(2)由图7知：声道10上游探头与声道1下游探头相隔较近,而声道10上游探头对流体产生的影响会波及到声道1下游探头附近的测量区域,导致该区域流体的流速降低。这一点也可以从声道1的速度分布看出(如图8)。相反,对于声道2、3、4、5来说,其下游探头与对称声道的上游探头距离较远,因此,几乎不受对称声道上游探头的影响。

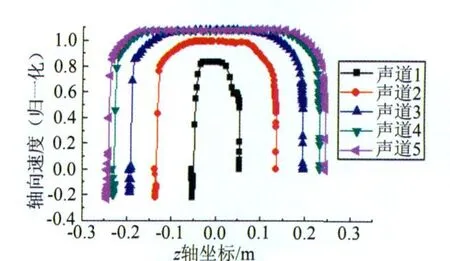
图8 测量段各声道的轴向速度分布Fig.8 Distribution of the axial velocity of each path

3.2.2 探头对测量精度的影响

探头对流场造成的影响会直接反映在测量误差上,以下将对这方面进行分析。

对于仿真来说,可以假设在测量段(流量计安装位置)上游1.5D处放置了一个理想的交叉9声道超声流量计,其探头前端面与管道内壁完全重合,即不对流体流场产生任何影响。该理想超声流量计的声路角、旋转角与测量段流量计完全相同。经计算上游1.5D处流量计的测量误差仅为-0.2195%,相对于测量段的测量误差来说,上游1.5D处流量计的误差可以忽略不计。测量段与上游1.5D处相比,导致两处测量结果存在差异的最主要因素就是探头。因此,可以将测量段与上游1.5D处进行对比来分析探头对测量误差的影响(¯Vi表示测量段流量计声道i的线平均速度;¯V1.5Di 表示上游1.5D处流量计声道i的线平均速度(i=1、2、3、……、18))。

上游1.5D处与测量段的结果对比如图9所示。

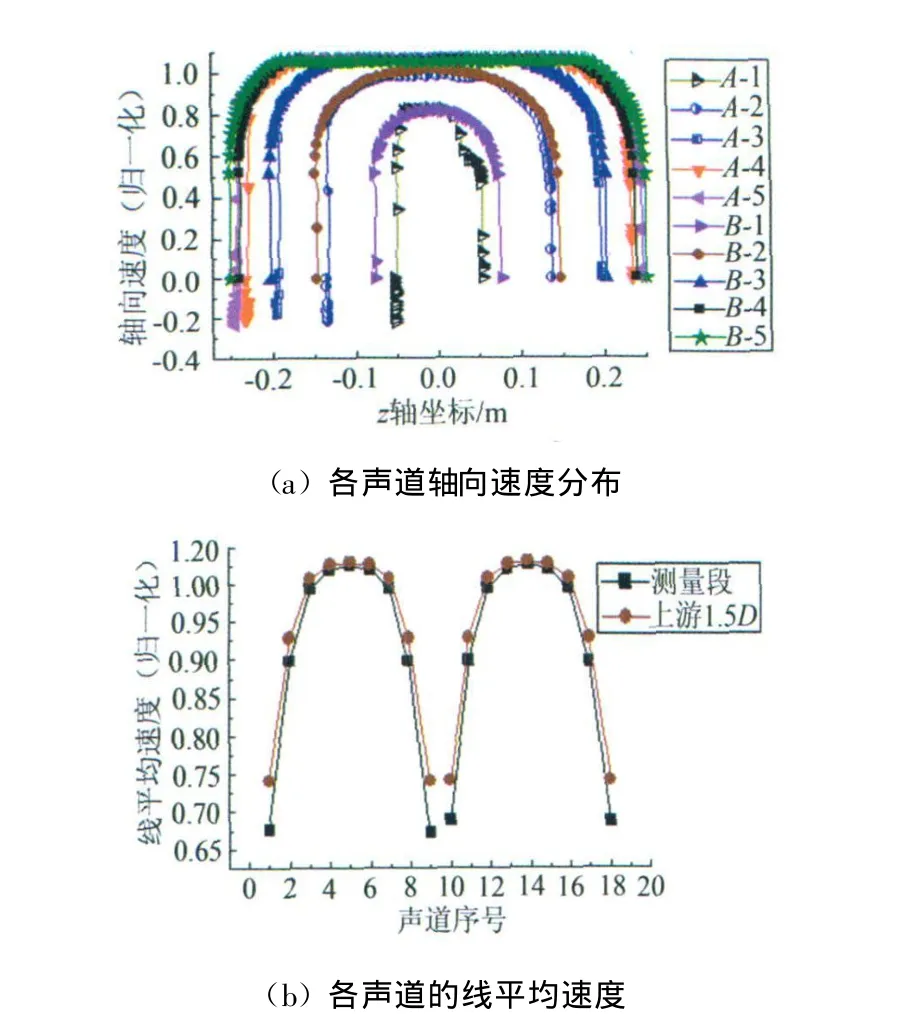
图9 测量段与上游1.5D处对比Fig.9 Comparison between results in the measuring section and 1.5D upstream

图9(a)图例中“A”、“B”分别表示“测量段”、“上游1.5D”;“1”、“2”、“3”、“4”、“5”表示声道序号。

(1)相对于上游1.5D处来说,由于测量段探头深入到管内,使得各声道长度Li变短。因此,测量段各声道的速度分布比上游1.5D处的范围窄(如图9(a));

(2)由图9(a)知,测量段声道中间部分的流速值与上游1.5D处的基本重合,但是其声道两端的流速值要小于上游1.5D处,且存在负的速度值。因此,导致¯Vi比¯V1.5Di要小;

(3)由于声道1、2的声道长度相对较短,因此, ¯V1、¯V2受到的影响较大,从而导致 ¯V1、¯V2明显小于¯V1.5D1 、¯V1.5D2 ;相反,由图9(b)可知,¯V3、¯V4、¯V5受到的影响相对较小。

综上,测量误差总是为负值的原因：由于探头影响流场,使探头附近产生回流,导致各声道的线平均速度减小。因此,流量测量值Q偏小,测量误差为负。

由表2知：相同口径条件下,入口速度越大(即Re越大),测量误差负值越大;当入口速度(或Re)达到一定范围时,测量误差基本不变。5种情况下,各声道线平均速度比较如图10所示。

靠近管道轴心声道(如声道4、5、6及13、14、15)的线平均速度随着入口速度的增大而逐渐减小,而远离管道轴心的声道正好相反;当入口速度增大到6m/ s后,各声道线平均速度基本重合(即图10中6m/s、8m/s)。这正好符合流体力学中湍流速度分布公式[12],即当雷诺数Re增大时,整个管道断面的速度分布越来越平坦,当Re达到一定范围后,整个断面的速度分布基本不再发生变化。

图10 不同流速下各声道线积分速度归一化比较Fig.10 Mean flow velocity(normalized)of each path under different inlet velocities

进一步分析,由Gauss-Jacobi方法[8-10]知：靠近管道轴心的声道加权系数wi较大,远离管道轴心的声道加权系数wi较小。又由公式(1)知：在D、Lwi、θi不变的情况下,靠近管道轴心声道的线平均速度将对积分流量Q起主要作用。所以,在远离管道轴心声道的线平均速度相差不大的情况下,靠近管道轴心声道的归一化线平均速度越大,则归一化积分流量值越大(更接近理论值),测量误差则越小。因此,由图10可知,随着入口速度(或Re)增大,归一化积分流量逐渐减小,即逐渐远离理论流量,误差逐渐增大;当入口速度(或Re)达到一定范围后,归一化积分流量趋于稳定,误差也趋于稳定(如表2)。

4 结 论

采用数值仿真方法对一台DN500超声流量计的测量性能进行了研究,讨论了其探头全伸位置安装时对流场及超声流量计测量性能的影响,分析了超声流量计在不同流速条件下测量误差的变化规律。主要得到以下结论：

(1)超声流量计探头插入管内,一方面使声道缩短,另一方面对管内流场产生了影响,会在探头附近产生回流。而超声流量计各声道正好经过这部分流场,使得各声道的线平均速度减小,进而使得积分流量值偏小,测量误差为负;

(2)探头全伸位置安装条件下,入口速度为0.3～8m/s时,测量误差为-1.25%～-1.9%。而且,当入口速度(或Re)增大时,测量误差也逐渐增大;当入口速度(或Re)达到一定范围后,测量误差基本趋于稳定;

(3)仿真结果与实验结果相比有0.16%的偏差,这是由于仿真中忽略了一些因素(如管道粗糙度等)。对于所讨论的复杂模型,这种差异是可以接受的。因此,文中提出的仿真方法可以作为今后研究此类问题的一个重要手段。

[1] WALSH J T.A report of acoustic transit time accuracy field work performed in North America[C].5th International Conference on Hydraulic Efficiency Measurements,Lucerne,2004.

[2] Measurement of gas by multipath ultrasonic meters[R]. American Gas Association.A.G.A.No.9,1998.

[3] 熊光德.新型天然气超声波流量计量技术[J].天然气与石油,2002,2(20)：57-61.

[4] 杉下钟尾,覃在清.提高多声道超声波流量计精度的修正方法[J].国外大电机,1994,(1)：95-100.

[5] VOSER A.Analyse und fehleroptimierung der mehrpfadigen akustischen durchflussmessung in asserkraftanlagen[D].Zürich：Diss.ETH,1999：92-123.

[6] VOSER A,BRUTTIN CH,PRÉNAT J E,et al.Improving acoustic flow measurement[J].International Water Power and Dam Construction,1996,48(4)：30-34.

[7] STAUBLI T,TRESCH T,GRUBER P.A discussion of uncertainties and of potential for improvement of the acoustic transit time method[C].Hydro,Porto,2004.

[8] ASME PTC 18-2002,Hydraulic turbines and pump-turbines[S].American Society of Mechanical Engineers, 2002.

[9] PRESS W H,Teukolsky S A.Numerical recipes in C [M].Cambridge University Press,1992：147-156.

[10]IEC41-1991.International code for the field acceptance test of hydraulic turbines[S].International Electrotechnical Commission,1991.

[11]BARTON N A,BROWN G J.Velocity distribution effects on ultrasonic flowmeters-Part 2 Determination by computational and experimental methods[R].Report No. 358/99,National Engineering Laboratory,1999.

[12]张也影.流体力学[M].北京：高等教育出版社,1999：236-272.