兆瓦级风力发电机主要承载螺栓强度的有限元计算
2011-04-12沃晓临马春翔
沃晓临,马春翔
(1.上海交通大学机械与动力工程学院,上海 200240;2.上海电气风电设备有限公司,上海 200030)
连接螺栓作为关系到风机结构安全的关键零件之一,需结合风机载荷特点,采用可靠、准确的计算方法对其校核,以提高风机整体可靠性,保证其在复杂外载荷下20年的工作寿命。风力机的风轮所受载荷包括风载和重力载荷,受载情况十分复杂。其中影响风轮风载的因素有垂直扫风面的稳态气流、存在偏航误差的气流、主轴的倾角、风切变、塔影效应、尾流影响等;影响风轮的重力载荷的因素有离心力、偏航动作时的陀螺载荷、风轮制动时的制动载荷、叶片挥舞带来的载荷等。由于载荷的复杂性,只考虑单一倾覆力矩或单一工作载荷的常用工程算法或准则计算方法,已经不能直接应用于风电行业。本文将结合风力机设计载荷的特点,依据德国船级社风力机认证导则GL2003的要求,使用ANSYS12.0软件,用数值仿真的方法,对兆瓦级风力发电机组的主轴与轮毂的连接螺栓进行计算。利用数值仿真的结果,对采用高强度螺栓工程计算标准VDI2230计算所得的计算应力进行修正,以得到更接近实际的计算值。在计算疲劳强度方面,基于由风电专业多体动力学软件计算所得的载荷时间序列,利用一般通用疲劳计算软件,采用通道组合的方法,将多个方向上的复杂载荷时间历程,在考虑螺栓连接的非线性因素的条件下,转换为螺栓上所受的应力时间序列。通过对应力时间序列的雨流计数后,得到最终的疲劳损伤。
1 计算模型
轮毂是风力机风轮毂的一部分,通过高强度螺栓直接与主轴连接,见图1和图2。同时,轮毂也是驱动链的一个组成部分,因此是风力发电机中受载最为复杂的部件,见表1。
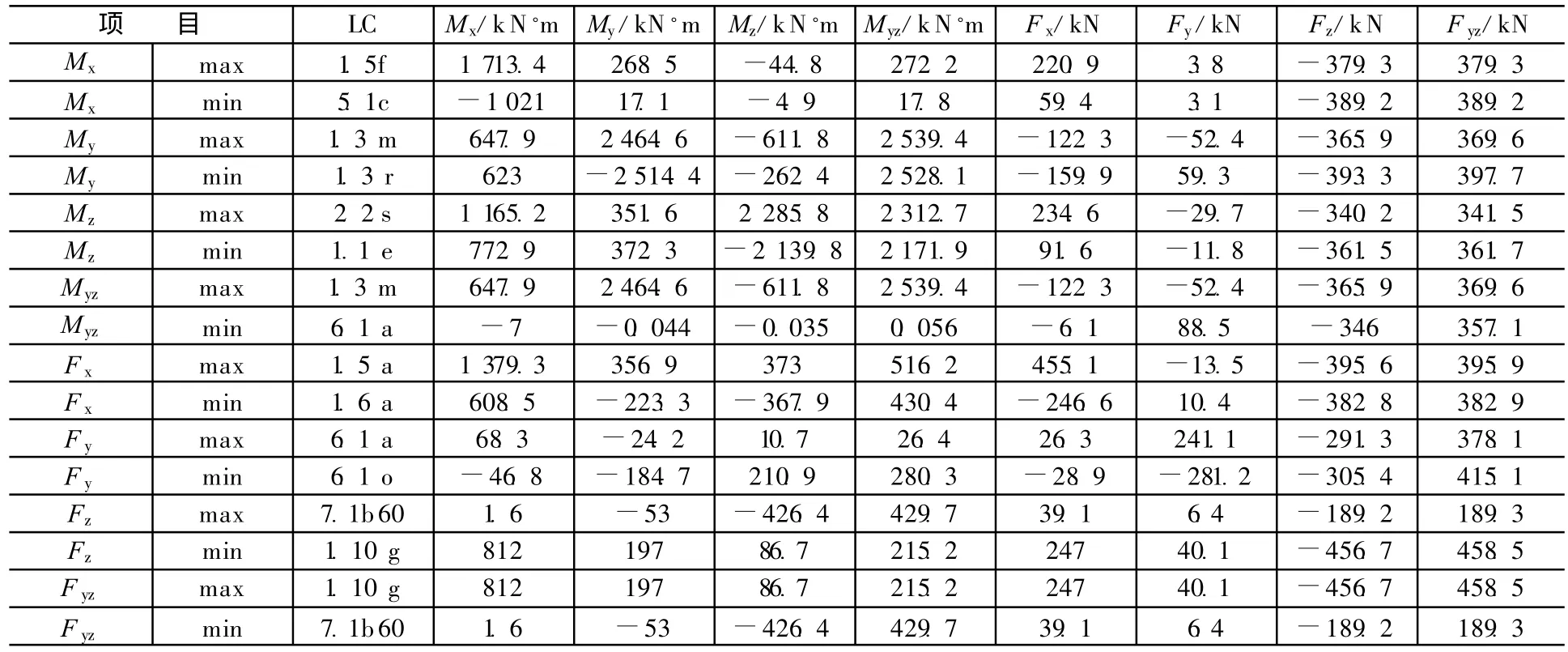
表1 轮毂中心极限载荷(固定坐标系) MPa

图1 铸造轮毂
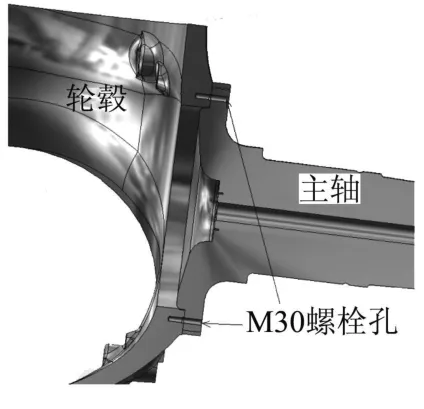
图2 轮毂与主轴连接
采用solidworks,对轮毂与主轴进行建模和装配。在ANSYS Workbench中分网导入经典界面形成计算用装配体,见图3。对螺栓采用梁单元模拟,见图4,两端分别按实际长度与主轴端面与轮毂实体单元做共节点连接。主轴与轮毂间采用标准接触。加载点设在轮毂中心,并以刚性单元与轮毂的三个法兰面相连。主轴端部做固支处理。计算采用的坐标系见图5。

图3 有限元模型
2 计算工况设计
为保证螺栓连接在极限工况与疲劳工况下的安全,必须分别计算极限强度与疲劳强度。

图4 螺栓的梁单元模拟
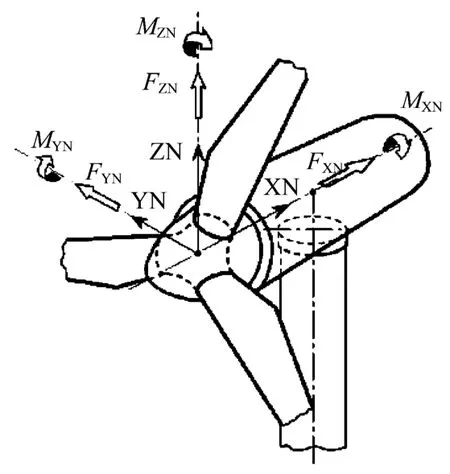
图5 计算坐标系
2.1 极限载荷工况
对于单个极限工况,在ansys12.0经典界面下设置2个载荷步,先对螺栓施加预紧力F M,再加对应设计极限工况的极限载荷。
1)载荷步一 根据VDI2230的要求,不同的装配方式须选用不同的加紧系数αA:

式中:FMZUL为螺栓对应的许用预拉伸力,按VDI2230表A1,取427 kN;在计算极限工况时,αA取1.0。
2)载荷步二 加载极限载荷。依据GL规范要求,按载荷计算所得的极限工况载荷加载,计算所用载荷见表1。根据连接需要按上述载荷计算所有16组工况。
2.2 疲劳计算工况
1)载荷步一 同极限工况,但参照实际安装工艺,考虑疲劳计算要求,αA取1.6。
2)载荷步二 添加倾覆力矩±My和±Mz设为6 MNm,得到实际四组工况,见表2。
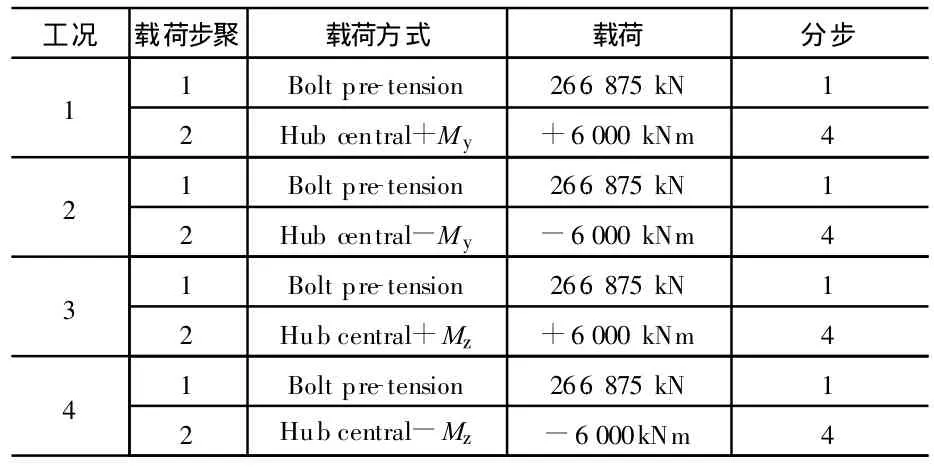
表2 疲劳工况计算载荷
3 数值计算结果分析
选取疲劳载荷计算任一工况载荷步一的计算结果分析,以验证模型准确性。
3.1 数值计算结果
图6为螺母接触区域的压应力分布的仿真结果,可以验证应力云图符合 VDI 2230,Figure 3.2/4.的假设。图7为任取的螺栓沿高度分布的轴向应力有限元计算结果。按工程算法:

式中:FM为实际施加的预紧力,266.875 MPa;D为螺栓工程直径。
所得估算应力σa为378 MPa,与有限元计算结果的误差为1.85%,证明模型有效。
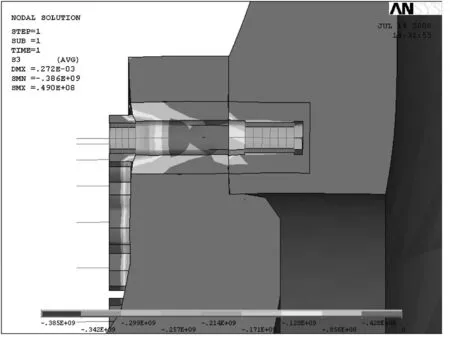
图6 螺栓附近区域第三主应力云图
3.2 极限结果后处理
根据VDI 2230,按Fmzul算螺栓最大预紧力:
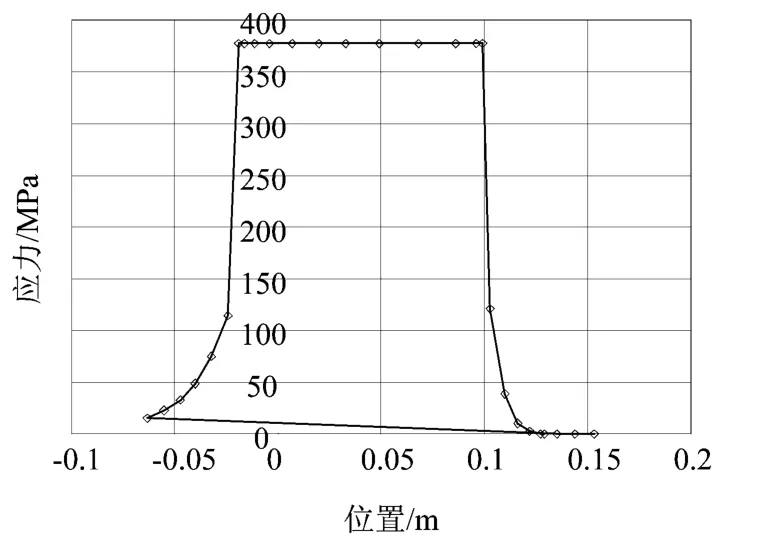
图7 螺栓轴向应力分布
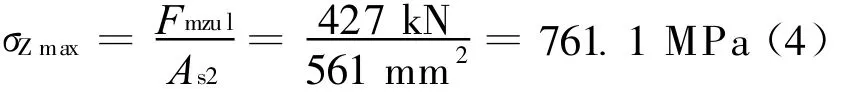
使用ANSYSapdl语言读取模型中各工况下螺栓的轴向及弯曲正应力,计算σres,FEA:
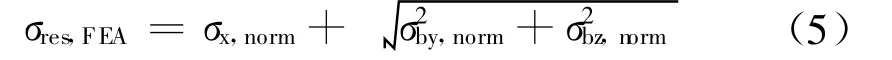
式中:σx,norm,σby,norm和σbz,norm是在FEA中螺栓最大应力位置三个方向应力大小,不包括螺栓预紧应力。减去螺栓预紧力的工作,在ANSYS中进行工况叠加实现。
最后根据VDI 2230:
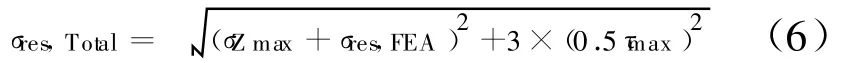
式中:σres,Total为螺栓工作应力,τmax为螺栓所受剪切力。
由于轮毂与主轴螺栓为非受剪螺栓,实际安装工艺也为液压拉伸,故在本例中认为τmax为0。如螺栓采用其他安装方法需按照其他相关规定考虑螺栓工作时的剪切应力影响。最后依据螺栓屈服强度计算出极限最终安全系数,见表3。
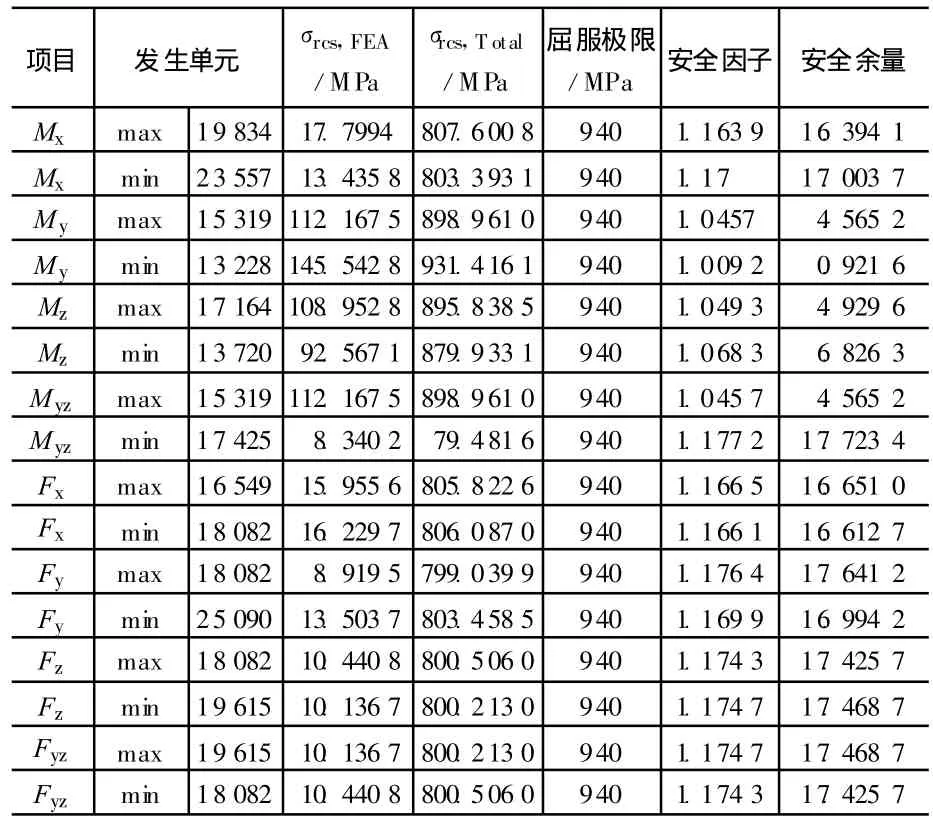
表3 螺栓静强度计算结果
从表3可知,最小安全裕读出现在M y负向最大的载荷工况,发生单元为13228。
3.3 疲劳结果后处理
复杂受多轴载荷的疲劳计算需基于时间序列载荷,所以要考虑轮毂与主轴连接螺栓复杂的受载情况,需要使用基于时间序列的载荷信息。由于扭转及沿主轴方向的载荷对连接处的应力变化范围影响不大,故在计算时仅考虑F y,F z,M y和M z四个方向上的载荷。通过有限元计算后得到连接螺栓σres,FEA与外载荷的非线性关系,见图8 (图中的螺栓应力均剔除了螺栓预紧力的影响),同时得到沿圆周方向螺栓应力的分布大小见图9。
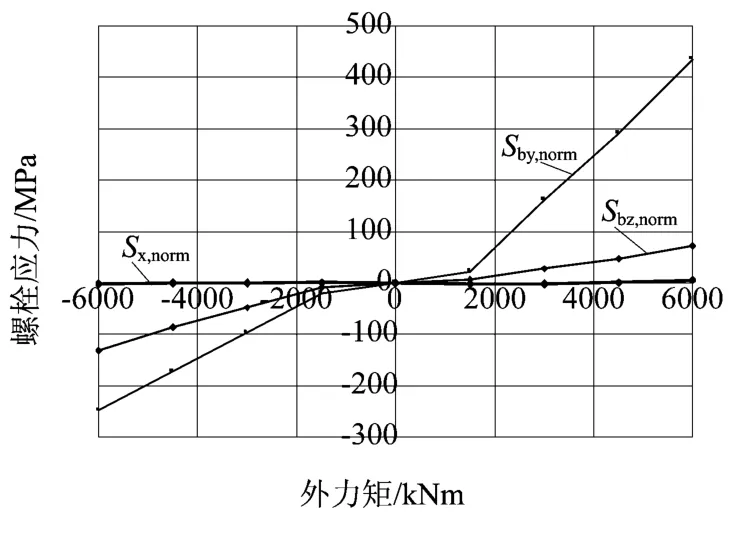
图8 应力与加载载荷的非线性关系
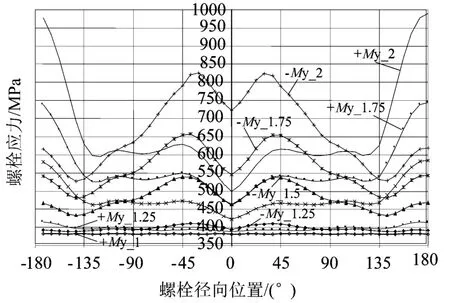
图9 不同周向螺栓应力在不同载荷步下的分布
通过ANSYS APDL命令,可得出不同位置螺栓对外载荷的响应曲线,从而找到在4个关键载荷分量下最危险的螺栓。从图9看,180°处的螺栓在收载时应力最大。经过比较全部4个疲劳载荷工况,找到另有位于螺栓分布圆位置-30°和-70°的螺栓对外载荷较敏感。
按照GL确定螺栓的疲劳等级DC见表4。
基于时间序列计算调整轮毂中心载荷:


表4 螺栓疲劳强度选取

式中;d为轮毂中心到螺栓连接处中心距离。
按螺栓与外载荷的非线性关系(图8),在专业疲劳计算软件中使用由式(7)和(8)修正后的时间序列,通过通道组合可以的到一条螺栓应力σres,Total的时间序列曲线。通过对此应力曲线进行雨流计数后,基于欧洲钢结构设计标准EU code 3的S-N曲线(图10),即可依据疲劳损伤累计的理论,得到危险位置的疲劳损伤,见表5。按上述方法可以得到危险位置处的损伤值均小于1。

图10 基于EU code 3所用的S-N曲线
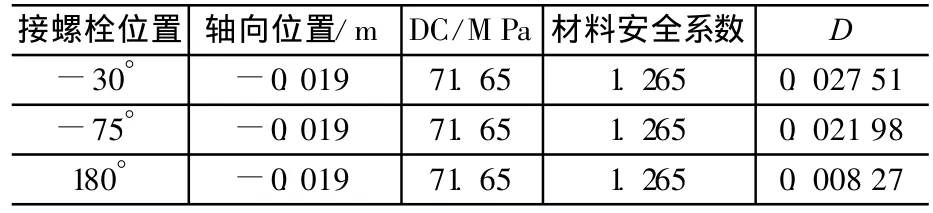
表5 疲劳损伤计算结果
4 结语
按以上方法进行计算的机组已成功在现场运行5年以上,通过每半年一次的风机例行检查,证实按此方案计算的螺栓连接安全可考。目前,相关机组的设计方案业已通过国内权威认证机构的认证。
