多粒度粗糙集与多源信息系统中的粗糙集模型

窦慧莉，於东军，杨习贝，

(1.江苏科技大学 计算机科学与工程学院，江苏镇江212003;2.南京理工大学 计算机科学与技术学院，南京210094)

0 引言

Pawlak根据实际工程应用的需求，在经典集合论的基础上，提出了粗糙集理论［1－4］。近年来，这一理论已被证实在模式识别、机器学习和自动知识获取等众多领域有着广泛而又突出的应用。

Pawlak定义了知识基的概念，在一个知识基中，有一族等价关系，所有这些等价关系的交集称为不可分辨关系，因而这个不可分辨关系依然是一个等价关系。在这个不可分辨关系的基础上，Pawlak给出了粗糙下近似和粗糙上近似的概念，使用已有的知识来近似地逼近未知的概念。

然而值得注意的是，Pawlak的粗糙集模型是建立在仅仅一个不可分辨关系的基础上的，钱宇华等人认为，在决策分析问题中，多个决策者之间的关系有可能是相互独立的，因而需采用多个二元关系来进行目标的近似逼近，为此他提出了多粒度粗糙集模型［5－6］的概念。在钱宇华的多粒度粗糙集模型中，他采用了两个及两个以上的不可分辨关系进行概念的近似逼近，并分析了多粒度粗糙集模型与经典粗糙集之间的关系。在钱宇华的多粒度粗糙集模型中，主要有两种不同的近似逼近方式，一种是乐观多粒度粗糙集方法，另一种是悲观多粒度粗糙集方法。

此外，从拓展信息系统的角度出发，Khan等人研究了多源信息系统［7］，一个多源信息系统实际上是一个信息系统族，在多源信息系统的框架下，Khan给出了强、弱下近似和强、弱上近似集合的概念。进一步研究可以发现，多粒度粗糙集模型中每一个不可分辨关系可以被看作是由一个信息系统中的属性子集构成的，因而从这个角度出发，可以讨论多粒度粗糙集模型与多源信息系统中粗糙集模型之间的关系。

本文主要内容安排如下:第一节介绍了乐观和悲观多粒度粗糙集模型，第二节给出了多粒度粗糙集模型的性质，第三节首先给出了多源信息系统中粗糙集模型的概念，然后证明了多源信息系统中的粗糙集模型是多粒度粗糙集的一种表示形式，第四节总结全文。

1 多粒度粗糙集

形式化地，一个信息系统可被定义为二元组S=＜U，AT＞，其中

(1)U表示所有对象的集合，称为论域;

(2)AT表示所有属性的集合。

对于∀a∈AT，定义映射a:U→Va，Va表示属性a的值域，即a(x)∈Va(x∈U)。

在信息系统S中，根据属性集合AT，可得到一个不可分辨关系，即等价关系形如

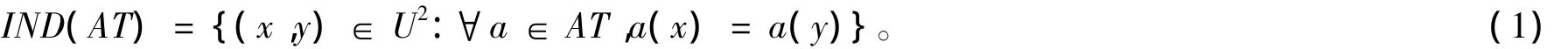
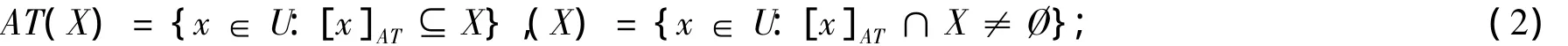
其中［x］AT={y∈U:(x，y)∈IND(AT)}表示U中所有与x具有不可分辨关系IND(AT)的对象的集合，即x的等价类。

定义2 令 S为一信息系统，A1，A2…Am⊆ AT，对于 ∀X⊆ U，X的乐观多粒度下近似集合与上近似集合分别定义为:

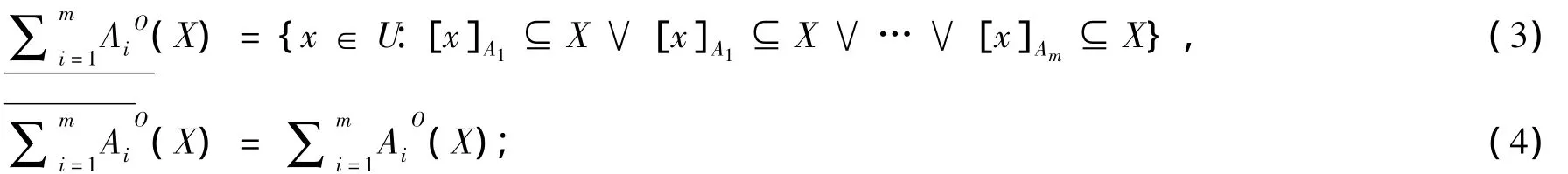
其中X表示集合X的补集。

定义3 令 S为一信息系统，A1，A2…Am⊆ AT，对于 ∀X⊆ U，X的悲观多粒度下近似集合与上近似集合分别定义为:

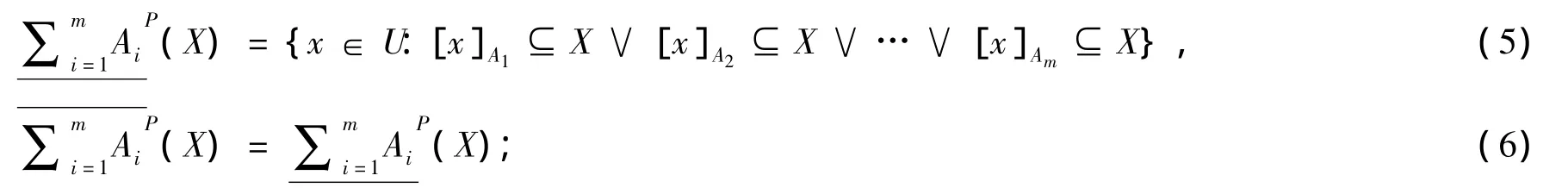
由定义2和定义3可以看出，乐观多粒度下近似要求至少有一个粒度层次上的等价类包含在目标概念中，而悲观多粒度下近似则要求所有粒度层次上的等价类都包含在目标概念中，因而悲观多粒度下近似的要求比乐观多粒度下近似的要求要更严格。乐观多粒度上近似和悲观多粒度上近似都是根据其下近似的补集加以定义的。据此，很容易得到如下所示的性质。

定理1 令S为一信息系统，A1，A2…Am⊆AT，对于∀X⊆U，有

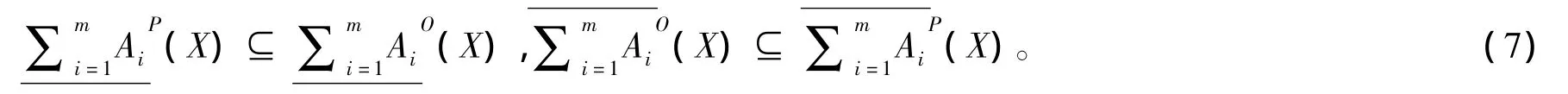
2 多粒度粗糙集模型的性质

定理2 令S为一信息系统，A1，A2…Am⊆AT，对于∀X⊆U，有

定理3 令S为一信息系统，A1，A2…Am⊆AT，对于∀X⊆U，有

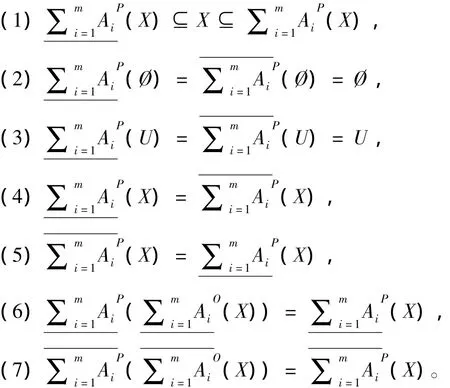
根据定理2和定理3可以看出，尽管多粒度粗糙集模型是构建在多个不可分辨关系的基础上的，但是乐观和悲观多粒度粗糙集模型仍然满足Pawlak经典粗糙集模型的相关性质。

3 多源信息系统与粗糙集

多源信息系统，顾名思义，是由一族信息系统构成的。形式化地，一个多源信息系统是一个信息系统族I={S1，S2，…，Sm}，其中S1，S2，…，Sm是m个信息系统，这些信息系统的定义如第一节所示。在多源信息系统中，Khan定义了强下近似集、弱下近似集、强上近似集、弱下近似集［7］，如定义3所示。

定义3 令I={S1，S2，…，Sm}为一多源信息系统，对于∀X⊆U，X的强下近似集、弱下近似集、强上近似集、弱下近似集分别记为且

通过对多粒度粗糙集模型和多源信息系统中的粗糙集模型对比分析发现，多源信息系统中的每一个信息系统实际上对应于多粒度粗糙集模型中的每一个属性集合，从这个角度出发，可以讨论这两者之间的关系。

定理4 令S为一信息系统，A1，A2…Am⊆AT，可构建一个多源信息系统I={S1，S2，…，Sm}，其中Ai表示信息系统Si(1≤i≤m)中的属性集合，因而对于∀X⊆U，有

证明:仅证式(12)，其他证明类似。根据定义2，对于∀X∈U，有

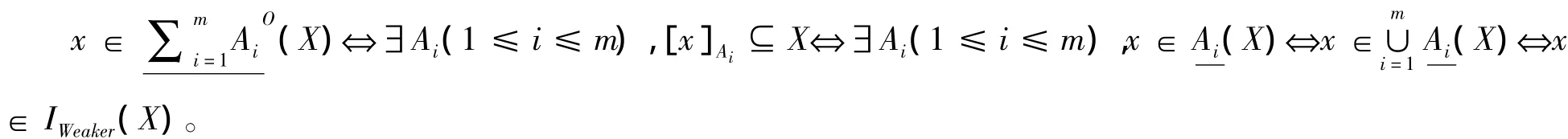
由定理4可以看出，多源信息系统中的每一个信息系统对应多粒度粗糙集模型中的每一个属性子集，因而乐观多粒度下近似与弱下近似等价，悲观多粒度下近似与强下近似等价，乐观多粒度上近似与强上近似等价，悲观多粒度上近似与弱上近似等价。根据这样的分析，我们可以得出结论，多源信息系统中的粗糙集就是多粒度粗糙集模型。

4 结束语

多粒度粗糙集模型的概念为粗糙集理论的发展注入了新的活力。多粒度粗糙集模型从多个相互独立的粒结构出发，与经典的粗糙集模型是有着本质的区别的。

本文主要研究了多粒度粗糙集模型与多源信息系统中粗糙集模型之间的关系，证明了多源信息系统中的粗糙集模型就是多粒度粗糙集的一种表示形式，因而可以说明多粒度粗糙集模型是一种更为广义的粗糙集形式。

在本文工作的基础上，笔者下一步的工作就是讨论多粒度粗糙集模型与其他扩展粗糙集模型的关系。

［1］Pawlak Z.Rough set theory and its applications to data analysis［J］.Cybernetics and Systems，1998，29:661 －688.

［2］Pawlak Z，Skowron A.Rudiments of rough sets［J］.Information Sciences，2007，177:3 －27.

［3］Pawlak Z，Skowron A.Rough sets:Some extensions［J］.Information Sciences，2007，177:28 －40.

［4］Pawlak Z，Skowron A.Rough sets and boolean reasoning［J］.Information Sciences，2007，177:41 －73.

［5］Qian Y，Liang J，Dang C.Incomplete multigranulation rough set［J］.IEEE Transactions on Systems，Man and Cybernetics，Part A，2010，20:420 －431.

［6］Qian Y，Liang J，Yao Y，et al.MGRS:A multi－ granulation rough set［J］.Information Sciences，2010，180(6):949 －970.

［7］Khan M，Banerjee M.Formal reasoning with rough sets in multiple － source approximation systems［J］.International Journal of Approximate Reasoning，2008，49:466 －477.